Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10 tập 2. Bài viết này sẽ hướng dẫn bạn giải bài 9 trang 18 SGK Toán 10 tập 2 – Chân trời sáng tạo một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập môn Toán.
Để quả bóng có thể ném được qua lưới cao 2 m, người ta phải đứng cách lưới bao xa? Làm tròn kết quả đến hàng phần mười
Đề bài
Quỹ đạo của một quả bóng được mô tả bằng hàm số \(y = f\left( x \right) = - 0,03{x^2} + 0,4x + 1,5\)
với y (tính bằng mét) là độ cao của quả bóng so với mặt đất khi độ dịch chuyển theo phương ngang của bóng là x (tính bằng mét). Để quả bóng có thể ném được qua lưới cao 2 m, người ta phải đứng cách lưới bao xa? Làm tròn kết quả đến hàng phần mười
Phương pháp giải - Xem chi tiết
Bước 1: Từ giả thiết lập bất phương trình
Bước 2: Giải bất phương trình vừa tìm được
Lời giải chi tiết
Để quả bóng có thể ném được qua lưới cao 2 m thì \(y = f\left( x \right) = - 0,03{x^2} + 0,4x + 1,5 > 2\)
\( \Rightarrow f\left( x \right) = - 0,03{x^2} + 0,4x - 0,5 > 0\)
Xét tam thức \(f\left( x \right) = - 0,03{x^2} + 0,4x - 0,5\) có \(\Delta = 0,1 > 0\), có hai nghiệm phân biệt là \({x_1} \simeq 1,4;{x_2} \simeq 11,9\) và có \(a = - 0,03 < 0\)
Ta có bảng xét dấu như sau
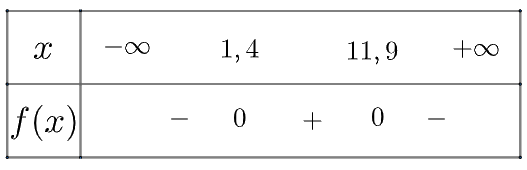
Vậy để quả bóng có thể ném được qua lưới cao 2 m, người ta phải đứng cách lưới từ 1,4 cho đến 11,9 mét
Bài 9 trang 18 SGK Toán 10 tập 2 – Chân trời sáng tạo thuộc chương trình học Toán 10, tập trung vào việc ứng dụng kiến thức về vectơ trong hình học. Bài tập này yêu cầu học sinh vận dụng các định lý, tính chất của vectơ để giải quyết các bài toán liên quan đến hình học phẳng. Việc nắm vững kiến thức nền tảng và kỹ năng giải toán là yếu tố then chốt để hoàn thành bài tập này một cách hiệu quả.
Bài 9 trang 18 SGK Toán 10 tập 2 – Chân trời sáng tạo thường bao gồm các dạng bài tập sau:
Để giúp bạn hiểu rõ hơn về cách giải bài tập này, chúng tôi sẽ trình bày lời giải chi tiết cho từng phần của bài tập. Lưu ý rằng, trong quá trình giải bài, bạn cần:
Đề bài: Cho hình bình hành ABCD. Gọi M là trung điểm của cạnh BC. Chứng minh rằng vectơ AM = (1/2) vectơ AB + vectơ AD.
Lời giải:
Ta có: vectơ AM = vectơ AB + vectơ BM. Vì M là trung điểm của BC nên vectơ BM = (1/2) vectơ BC. Mà vectơ BC = vectơ AD (do ABCD là hình bình hành). Do đó, vectơ AM = vectơ AB + (1/2) vectơ AD.
Sau khi nắm vững cách giải bài 9 trang 18 SGK Toán 10 tập 2 – Chân trời sáng tạo, bạn có thể tự giải các bài tập tương tự để củng cố kiến thức. Dưới đây là một số gợi ý:
Để học tập môn Toán 10 hiệu quả hơn, bạn có thể tham khảo thêm các tài liệu sau:
Bài 9 trang 18 SGK Toán 10 tập 2 – Chân trời sáng tạo là một bài tập quan trọng giúp bạn rèn luyện kỹ năng vận dụng kiến thức về vectơ vào giải quyết các bài toán hình học. Hy vọng rằng, với lời giải chi tiết và các gợi ý trên, bạn sẽ tự tin hơn trong quá trình học tập môn Toán.