Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 41, 42, 43 sách giáo khoa Toán 10 tập 1 - Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong học tập.
Bản tin dự báo thời tiết cho biết nhiệt độ ở một số thời điểm trong ngày 01/5/2021 tại thành phố Hồ Chí Minh đã được ghi lại thành bảng kèm với biểu đồ bên. Một thiết bị đã ghi lại vận tốc v (mét/giây) ở thời điểm t (giây) của một vật chuyển động như trong bảng sau:
Một thiết bị đã ghi lại vận tốc v (mét/giây) ở thời điểm t (giây) của một vật chuyển động như trong bảng sau:
t (giây) | 0,5 | 1 | 1,2 | 1,8 | 2,5 |
v (mét/giây) | 1,5 | 3 | 0 | 5,4 | 7,5 |
Vì sao bảng này biểu thị một hàm số? Tìm tập xác định của hàm số này.
Phương pháp giải:
Ta gọi y là hàm số của biến số x nếu với mỗi giá trị x thuộc D, ta xác định được một và chỉ một giá trị tương ứng y thuộc tập hợp số thực \(\mathbb{R}\).
Tập D được gọi là tập xác định.
Lời giải chi tiết:
Từ bảng giá trị vận tốc v (mét/giây) ở thời điểm t (giây) của vật chuyển động, ta thấy ứng với mỗi thời điểm t (giây) trong bảng đều có một giá trị vận tốc v duy nhất. Vì vậy, bảng này biểu thị một hàm số.
Hàm số đó có tập xác định \(D = \{ 0,5;1;1,2;1,8;2,5\} \)
Tìm tập xác định của các hàm số sau:
a) \(f(x) = \sqrt {2x + 7} \)
b) \(f(x) = \frac{{x + 4}}{{{x^2} - 3x + 2}}\)
Phương pháp giải:
Tập xác định của hàm số \(y = f(x)\) là tập hợp tất cả các số thực x sao cho biểu thức \(f(x)\) có nghĩa.
a) \(\sqrt A \) có nghĩa \( \Leftrightarrow A \ge 0\)
b) \(\frac{A}{B}\) có nghĩa \( \Leftrightarrow B \ne 0\)
Lời giải chi tiết:
a) Biểu thức \(f(x)\) có nghĩa khi và chỉ khi \(2x + 7 \ge 0,\)tức là khi \(x \ge \frac{{ - 7}}{2}.\)
Vậy tập xác định của hàm số này là \(D = \left[ { - \frac{7}{2}; + \infty )} \right.\)
b) Biểu thức \(f(x)\) có nghĩa khi và chỉ khi \({x^2} - 3x + 2 \ne 0,\)tức là khi \(x \ne 2,x \ne 1.\)
Vậy tập xác định của hàm số này là \(D = \mathbb{R}\backslash \left\{ {1;2} \right\}\)
Lời giải chi tiết:
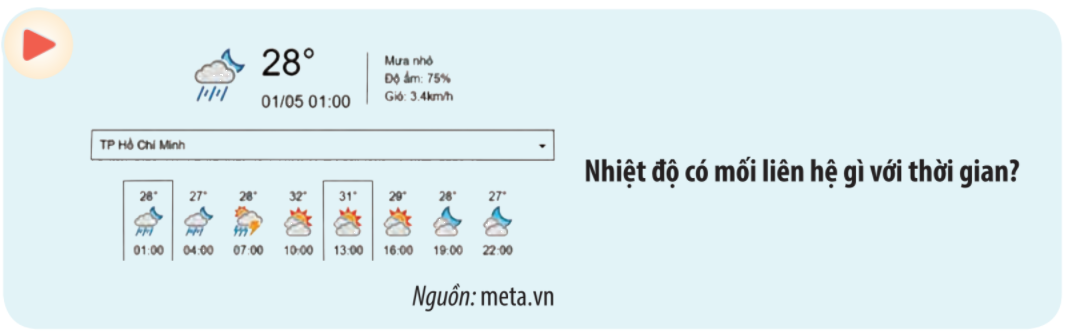
Mỗi thời điểm (giờ) chỉ có một nhiệt độ dự báo nhất định.
Nhiệt độ dự báo là một đại lượng phụ thuộc vào thời điểm (giờ).
Mối liên hệ giữa hai đại lượng này (nhiệt độ và thời gian) có đặc trưng của một hàm số.
Bản tin dự báo thời tiết cho biết nhiệt độ ở một số thời điểm trong ngày 01/5/2021 tại thành phố Hồ Chí Minh đã được ghi lại thành bảng kèm với biểu đồ bên.
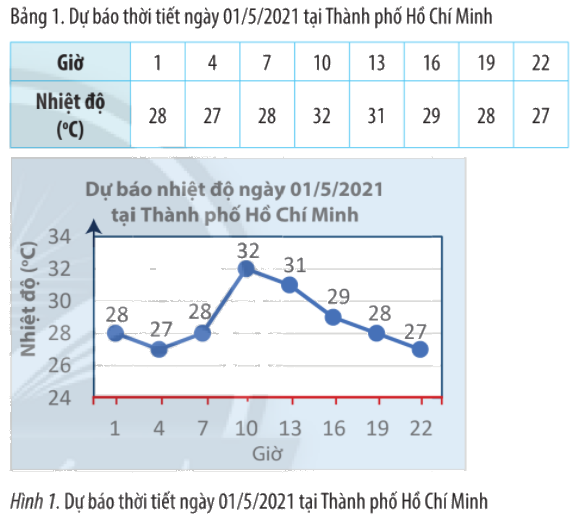
Sử dụng bảng hoặc biểu đồ, hãy:
a) Viết tập hợp các mốc đã có dự báo nhiệt độ.
b) Viết tập hợp các số đo nhiệt độ đã dự báo.
c) Cho biết nhiệt độ dự báo tại Thành phố Hồ Chí Minh vào lúc 7 giờ sáng ngày 01/5/2021.
Lời giải chi tiết:
a) Tập hợp các mốc giờ đã có dự báo nhiệt độ là:
\(A = \{ 1;4;7;10;13;16;19;22\} \)
b) Tập hợp các số đo nhiệt độ đã dự báo là:
\(B = \{ 28;27;32;31;29\} \)
c) Dự báo tại Thành phố Hồ Chí Minh vào lúc 7 giờ sáng ngày 01/5/2021 nhiệt độ là \({28^o}C.\)
Ở góc của miếng đất hình chữ nhật, người ta làm một bồn hoa có dạng một phần tư hình tròn với bán kính r (Hình 2). Bán kính bồn hoa có kích thước từ 0,5 m đến 3 m.

a) Viết công thức của hàm số biểu thị diện tích bồn hoa theo bán kính r và tìm tập xác định của hàm số này.
b) Bán kính bồn hoa bằng bao nhiêu thì nó có diện tích là \(0,5\pi \;{m^2}?\)
Phương pháp giải:
a) Diện tích hình tròn \(S = \pi {r^2}\)
Gọi x là biến số thể hiện kích thước của bán kính, từ đó suy ra công thức hàm số tính diện tích bồn hoa (một phần tư hình tròn) theo x.
Tập xác định là tập hợp các kích thước của bán kính bồn hoa.
b) Cho \(f(x) = 0,5\pi \;({m^2})\), tìm x.
Lời giải chi tiết:
a) Diện tích một phần tư hình tròn là: \(\frac{1}{4}\pi {r^2}\)
Gọi x là biến số thể hiện kích thước của bán kính.
Công thức hàm số tính diện tích bồn hoa là: \(f(x) = \frac{1}{4}\pi {x^2}\)
+) Vì bán kính bồn hoa có kích thước từ 0,5 m đến 3 m nên \(0,5 \le x \le 3\)
Vậy tập xác định của hàm số này là \(D = [0,5;3]\)
b) Diện tích là \(0,5\pi \;{m^2}\) tức là\(f(x) = 0,5\pi \;\)
\( \Leftrightarrow \frac{1}{4}\pi {x^2} = 0,5\pi \Leftrightarrow {x^2} = 2 \Rightarrow x = \sqrt 2 \) (do \(0,5 \le x \le 3\))
Vậy bán kính bồn hoa bằng \(\sqrt 2 \;m\).
Lời giải chi tiết:
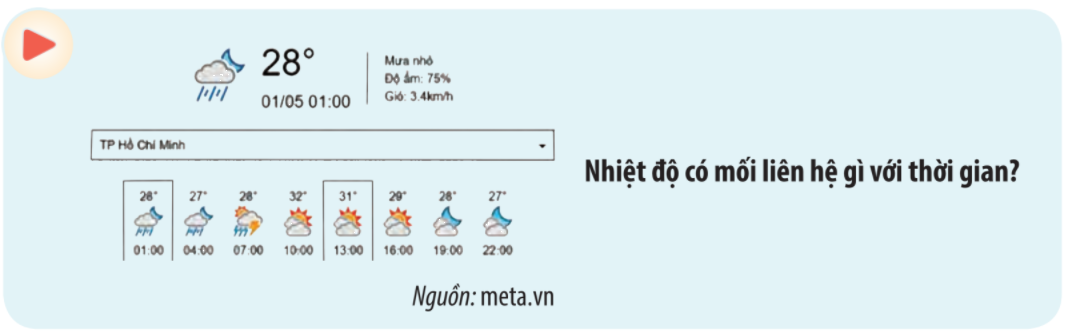
Mỗi thời điểm (giờ) chỉ có một nhiệt độ dự báo nhất định.
Nhiệt độ dự báo là một đại lượng phụ thuộc vào thời điểm (giờ).
Mối liên hệ giữa hai đại lượng này (nhiệt độ và thời gian) có đặc trưng của một hàm số.
Bản tin dự báo thời tiết cho biết nhiệt độ ở một số thời điểm trong ngày 01/5/2021 tại thành phố Hồ Chí Minh đã được ghi lại thành bảng kèm với biểu đồ bên.
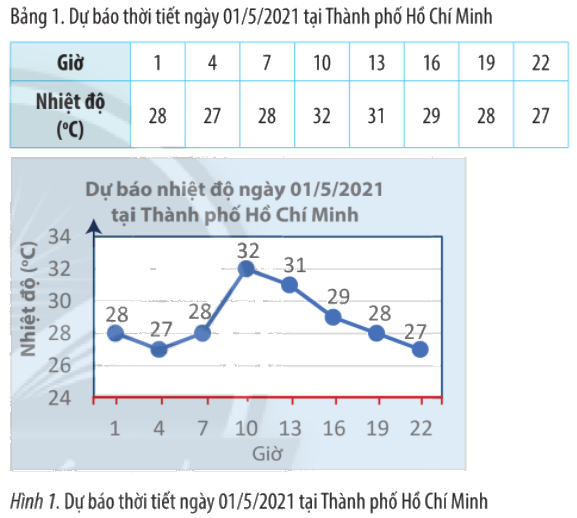
Sử dụng bảng hoặc biểu đồ, hãy:
a) Viết tập hợp các mốc đã có dự báo nhiệt độ.
b) Viết tập hợp các số đo nhiệt độ đã dự báo.
c) Cho biết nhiệt độ dự báo tại Thành phố Hồ Chí Minh vào lúc 7 giờ sáng ngày 01/5/2021.
Lời giải chi tiết:
a) Tập hợp các mốc giờ đã có dự báo nhiệt độ là:
\(A = \{ 1;4;7;10;13;16;19;22\} \)
b) Tập hợp các số đo nhiệt độ đã dự báo là:
\(B = \{ 28;27;32;31;29\} \)
c) Dự báo tại Thành phố Hồ Chí Minh vào lúc 7 giờ sáng ngày 01/5/2021 nhiệt độ là \({28^o}C.\)
Một thiết bị đã ghi lại vận tốc v (mét/giây) ở thời điểm t (giây) của một vật chuyển động như trong bảng sau:
t (giây) | 0,5 | 1 | 1,2 | 1,8 | 2,5 |
v (mét/giây) | 1,5 | 3 | 0 | 5,4 | 7,5 |
Vì sao bảng này biểu thị một hàm số? Tìm tập xác định của hàm số này.
Phương pháp giải:
Ta gọi y là hàm số của biến số x nếu với mỗi giá trị x thuộc D, ta xác định được một và chỉ một giá trị tương ứng y thuộc tập hợp số thực \(\mathbb{R}\).
Tập D được gọi là tập xác định.
Lời giải chi tiết:
Từ bảng giá trị vận tốc v (mét/giây) ở thời điểm t (giây) của vật chuyển động, ta thấy ứng với mỗi thời điểm t (giây) trong bảng đều có một giá trị vận tốc v duy nhất. Vì vậy, bảng này biểu thị một hàm số.
Hàm số đó có tập xác định \(D = \{ 0,5;1;1,2;1,8;2,5\} \)
Tìm tập xác định của các hàm số sau:
a) \(f(x) = \sqrt {2x + 7} \)
b) \(f(x) = \frac{{x + 4}}{{{x^2} - 3x + 2}}\)
Phương pháp giải:
Tập xác định của hàm số \(y = f(x)\) là tập hợp tất cả các số thực x sao cho biểu thức \(f(x)\) có nghĩa.
a) \(\sqrt A \) có nghĩa \( \Leftrightarrow A \ge 0\)
b) \(\frac{A}{B}\) có nghĩa \( \Leftrightarrow B \ne 0\)
Lời giải chi tiết:
a) Biểu thức \(f(x)\) có nghĩa khi và chỉ khi \(2x + 7 \ge 0,\)tức là khi \(x \ge \frac{{ - 7}}{2}.\)
Vậy tập xác định của hàm số này là \(D = \left[ { - \frac{7}{2}; + \infty )} \right.\)
b) Biểu thức \(f(x)\) có nghĩa khi và chỉ khi \({x^2} - 3x + 2 \ne 0,\)tức là khi \(x \ne 2,x \ne 1.\)
Vậy tập xác định của hàm số này là \(D = \mathbb{R}\backslash \left\{ {1;2} \right\}\)
Ở góc của miếng đất hình chữ nhật, người ta làm một bồn hoa có dạng một phần tư hình tròn với bán kính r (Hình 2). Bán kính bồn hoa có kích thước từ 0,5 m đến 3 m.

a) Viết công thức của hàm số biểu thị diện tích bồn hoa theo bán kính r và tìm tập xác định của hàm số này.
b) Bán kính bồn hoa bằng bao nhiêu thì nó có diện tích là \(0,5\pi \;{m^2}?\)
Phương pháp giải:
a) Diện tích hình tròn \(S = \pi {r^2}\)
Gọi x là biến số thể hiện kích thước của bán kính, từ đó suy ra công thức hàm số tính diện tích bồn hoa (một phần tư hình tròn) theo x.
Tập xác định là tập hợp các kích thước của bán kính bồn hoa.
b) Cho \(f(x) = 0,5\pi \;({m^2})\), tìm x.
Lời giải chi tiết:
a) Diện tích một phần tư hình tròn là: \(\frac{1}{4}\pi {r^2}\)
Gọi x là biến số thể hiện kích thước của bán kính.
Công thức hàm số tính diện tích bồn hoa là: \(f(x) = \frac{1}{4}\pi {x^2}\)
+) Vì bán kính bồn hoa có kích thước từ 0,5 m đến 3 m nên \(0,5 \le x \le 3\)
Vậy tập xác định của hàm số này là \(D = [0,5;3]\)
b) Diện tích là \(0,5\pi \;{m^2}\) tức là\(f(x) = 0,5\pi \;\)
\( \Leftrightarrow \frac{1}{4}\pi {x^2} = 0,5\pi \Leftrightarrow {x^2} = 2 \Rightarrow x = \sqrt 2 \) (do \(0,5 \le x \le 3\))
Vậy bán kính bồn hoa bằng \(\sqrt 2 \;m\).
Mục 1 của chương trình Toán 10 tập 1 - Chân trời sáng tạo tập trung vào việc giới thiệu các khái niệm cơ bản về tập hợp, các phép toán trên tập hợp, và các tính chất của chúng. Đây là nền tảng quan trọng để học sinh có thể tiếp cận các kiến thức phức tạp hơn trong các chương tiếp theo.
Bài tập này yêu cầu học sinh xác định các tập hợp, thực hiện các phép toán hợp, giao, hiệu, bù của các tập hợp, và chứng minh các tính chất liên quan. Để giải các bài tập này, học sinh cần nắm vững định nghĩa và các quy tắc của các phép toán trên tập hợp.
Bài tập này yêu cầu học sinh chứng minh các tính chất của phép hợp và phép giao, như tính giao hoán, tính kết hợp, tính phân phối. Để giải các bài tập này, học sinh cần sử dụng các định nghĩa và các quy tắc của các phép toán trên tập hợp.
Bài tập này yêu cầu học sinh áp dụng các kiến thức đã học để giải các bài toán thực tế. Các bài toán này thường liên quan đến việc sử dụng tập hợp để mô tả các đối tượng và các mối quan hệ giữa chúng.
| Tập hợp | Phép toán | Kết quả |
|---|---|---|
| A = {a, b, c} | B = {b, c, d} | A ∪ B = {a, b, c, d} |
| A = {1, 2, 3} | B = {3, 4, 5} | A ∩ B = {3} |
Để giải các bài tập về tập hợp hiệu quả, học sinh cần:
Ngoài sách giáo khoa, học sinh có thể tham khảo thêm các tài liệu sau:
Hy vọng rằng với lời giải chi tiết và các lời khuyên trên, các em học sinh sẽ tự tin hơn trong việc giải các bài tập về tập hợp và các phép toán trên tập hợp. Chúc các em học tập tốt!