Biểu diễn miền nghiệm của các bất phương trình sau trên mặt phẳng tọa độ Oxy: a) - x + y + 2 > 0
Đề bài
Biểu diễn miền nghiệm của các bất phương trình sau trên mặt phẳng tọa độ Oxy:
a) \( - x + y + 2 > 0\)
b) \(y + 2 \ge 0\)
c) \( - x + 2 \le 0\)
Lời giải chi tiết
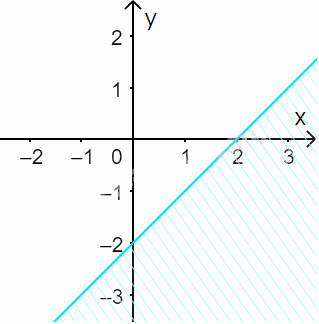
a) Vẽ đường thẳng \(\Delta : - x + y + 2 = 0\) đi qua hai điểm \(A(2;0)\) và \(B\left( {0; - 2} \right)\)
Xét gốc tọa độ \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \( - 0 + 0 + 2 = 2 > 0\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng không kể bờ \(\Delta \), chứa gốc tọa độ O
(miền không gạch chéo trên hình)
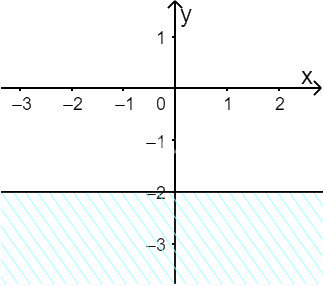
b) Vẽ đường thẳng \(\Delta :y + 2 = 0\) đi qua hai điểm \(A(0; - 2)\) và \(B\left( {1; - 2} \right)\)
Xét gốc tọa độ \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \(0 + 2 = 2 > 0\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng kể cả bờ \(\Delta \), chứa gốc tọa độ O
(miền không gạch chéo trên hình)
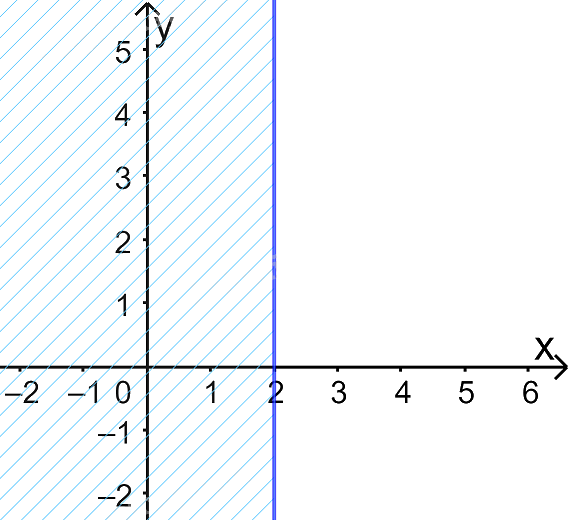
c) Vẽ đường thẳng \(\Delta : - x + 2 = 0\) đi qua hai điểm \(A(2;0)\) và \(B\left( {2;1} \right)\)
Xét gốc tọa độ \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \( - 0 + 2 = 2 > 0\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng kể cả bờ \(\Delta \), không chứa gốc tọa độ O
(miền không gạch chéo trên hình)