Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 4 trang 54, 55 SGK Toán 10 tập 1 chương trình Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập một cách khoa học và hiệu quả.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, tự tin giải quyết các bài toán Toán 10 và đạt kết quả tốt nhất trong học tập.
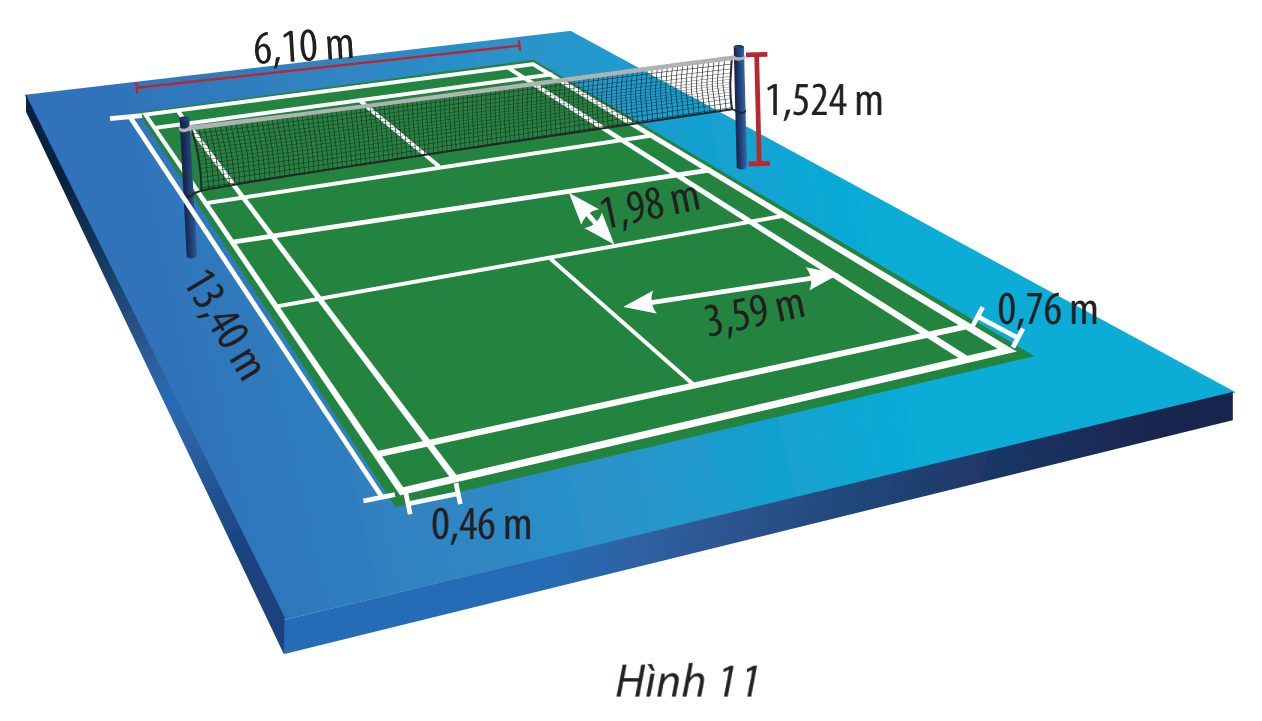
Trong bài toán ứng dụng, khi chơi trên sân cầu lông đơn, các lần phát cầu với thông tin như sau có được xem là hợp lệ không? (Các thông tin không được đề cập thì vẫn giữ như trong giả thiết bài toán trên) a) Vận tốc xuất phát của cầu là 12 m/s b) Vị trí phát cầu cách mặt đất 1,3 m. Lưu ý: Các thông số về sân cầu lông đơn được cho trong Hình 11.
Đề bài
Vận dụng trang 55 SGK Toán 10 tập 1 – Chân trời sáng tạo
Trong bài toán ứng dụng, khi chơi trên sân cầu lông đơn, các lần phát cầu với thông tin như sau có được xem là hợp lệ không? (Các thông tin không được đề cập thì vẫn giữ như trong giả thiết bài toán trên)
a) Vận tốc xuất phát của cầu là 12 m/s
b) Vị trí phát cầu cách mặt đất 1,3 m.
Lưu ý: Các thông số về sân cầu lông đơn được cho trong Hình 11.
Phương pháp giải - Xem chi tiết
Lần phát cầu được xem là hợp lệ nếu cầu ở trên mặt lưới (tại vị trí lưới phân cách) và điểm rơi không ra khỏi đường biên cuối sân đối phương.
Lập phương trình quỹ đạo của cầu lông: \(y = \frac{{ - g{x^2}}}{{2.{v_0}^2.{{\cos }^2}\alpha }} + \tan (\alpha ).x + {y_0}\)
a) Chỉ ra điểm rơi của cầu nằm ngoài đường biên ngoài bằng cách tính khoảng cách từ vị trí phát cầu đến vị trí cầu rơi
b) Tìm tung độ của điểm (có hoành độ là điểm đặt lưới phân cách) với độ cao của lưới.
Tính khoảng cách từ vị trí phát cầu đến vị trí cầu rơi xem cầu có thuộc khu vực được tính là hợp lệ hay không.
Lời giải chi tiết
a)
Chọn hệ trục tọa độ như Hình 9 (vị trí rơi của cầu thuộc trục hoành và vị trí cầu rời mặt vợt thuộc trục tung).
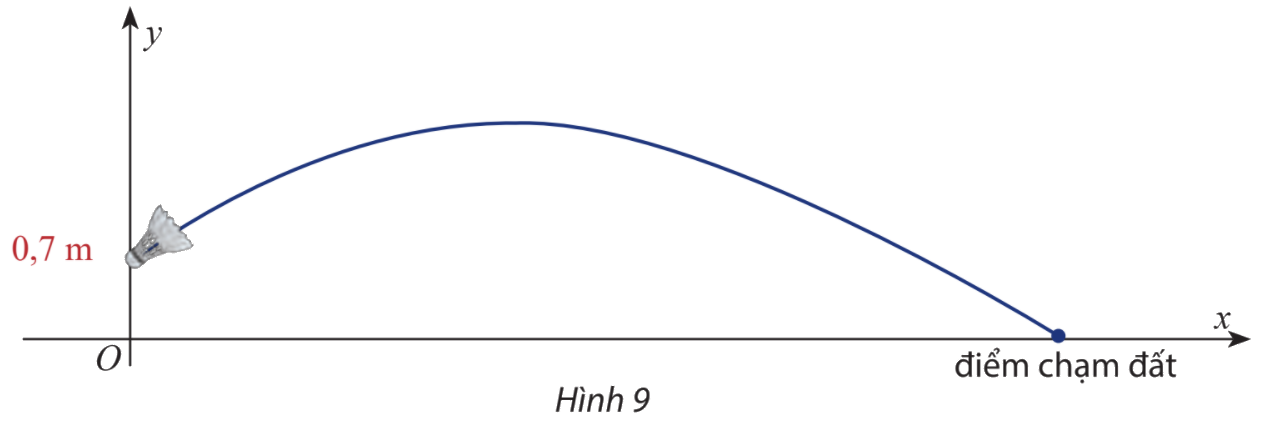
Với \(g = 9,8\;m/{s^2}\), góc phát cầu \(\alpha = {30^o}\), vận tốc ban đầu \({v_0} = 12\;m/s\), phương trình quỹ đạo của cầu là:
\(y = \frac{{ - 9,8}}{{{{2.12}^2}.{{\left( {\frac{{\sqrt 3 }}{2}} \right)}^2}}}{x^2} + \frac{{\sqrt 3 }}{3}.x + 0,7 = - \frac{{4,9}}{{108}}{x^2} + \frac{{\sqrt 3 }}{3}.x + 0,7\)
Vị trí cầu rơi chạm đất là giao điểm của parabol và trục hoành nên giải phương trình \( - \frac{{4,9}}{{108}}{x^2} + \frac{{\sqrt 3 }}{3}.x + 0,7 = 0\) ta được \({x_1} \approx - 1,11\) và \({x_2} \approx 13,84\)
Giá trị nghiệm dương cho ta khoảng cách từ vị trí người chơi cầu lông đến vị trí cầu rơi chạm đất là 13,84 m > 13,4 m (chiều dài cả sân)
Vậy lần phát cầu đã bị hỏng vì điểm rơi của cầu nằm ngoài đường biên ngoài.
b)
Ta so sánh tung độ của điểm trên quỹ đạo (có hoành động bằng khoảng cách từ điểm phát cầu đến chân lưới phân cách) với chiều cao mép trên của lưới.
Với \(g = 9,8\;m/{s^2}\), góc phát cầu \(\alpha = {30^o}\), vận tốc ban đầu \({v_0} = 8\;m/s\), vị trí phát cầu cách mặt đất 1,3 m. Phương trình quỹ đạo của cầu là:
\(y = \frac{{ - 9,8}}{{{{2.8}^2}.{{\left( {\frac{{\sqrt 3 }}{2}} \right)}^2}}}{x^2} + \frac{{\sqrt 3 }}{3}.x + 1,3 = - \frac{{4,9}}{{48}}{x^2} + \frac{{\sqrt 3 }}{3}.x + 1,3\)
Khi \(x = 4,\)ta có \(y = - \frac{{4,9}}{{48}}{.4^2} + \frac{{\sqrt 3 }}{3}.4 + 1,3 \approx 1,98 > 1,524\)
Vậy quỹ đạo của cầu cao hơn mép trên của lưới.
Tiếp theo ta kiểm tra vị trí cầu rơi có vượt đường biên ngoài hoặc chưa tới đường biên trong hay không.
Vị trí cầu rơi chạm đất là giao điểm của parabol và trục hoành nên giải phương trình \(y = \frac{{ - 9,8}}{{{{2.8}^2}.{{\left( {\frac{{\sqrt 3 }}{2}} \right)}^2}}}{x^2} + \frac{{\sqrt 3 }}{3}.x + 1,3 = - \frac{{4,9}}{{48}}{x^2} + \frac{{\sqrt 3 }}{3}.x + 1,3\) ta được \({x_1} \approx - 1,73\) và \({x_2} \approx 7,38\)
Giá trị nghiệm dương cho ta khoảng cách từ vị trí người chơi cầu lông đến vị trí cầu rơi chạm đất là 7.38 m.
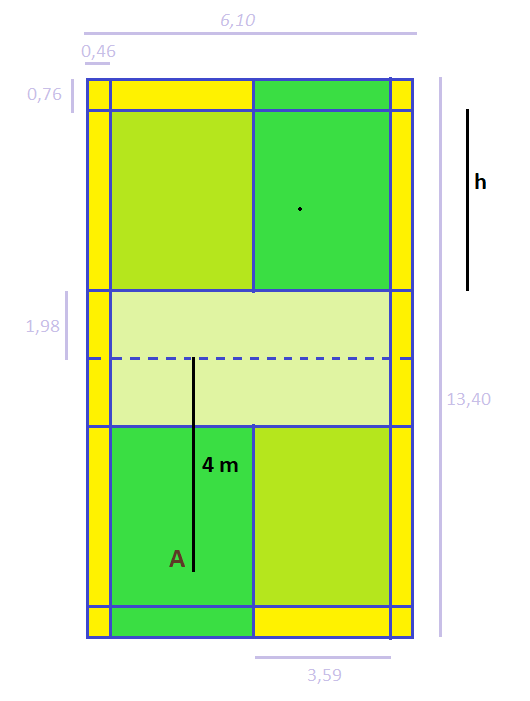
Dễ thấy: độ dài h (chiều dài của khu vực hợp lệ) là: \(13,4:2 - 1,98 -0,76= 3,96\) (m).
Do đó lần phát là hợp lệ nếu khoảng cách từ vị trí phát đến điểm rơi thuộc khoảng \(4 + 1,98 = 5,98(m)\) và \(4 + 1,98 +3,96= 9,94(m)\) và \(5,98 < 7,38 < 9,94\).
Như vậy vị trí quả cầu trên mặt đất nằm giữa đường biên trong và đường biên ngoài.
Kết luận: lần phát cầu này được coi là hợp lệ.
Mục 4 của SGK Toán 10 tập 1 chương trình Chân trời sáng tạo tập trung vào các kiến thức về vectơ, đặc biệt là các phép toán trên vectơ như cộng, trừ, nhân với một số thực và tích vô hướng của hai vectơ. Việc nắm vững các khái niệm và kỹ năng này là nền tảng quan trọng để học tốt các chương tiếp theo của môn Toán 10.
Bài tập mục 4 trang 54, 55 SGK Toán 10 tập 1 Chân trời sáng tạo bao gồm các dạng bài tập khác nhau, từ việc xác định tọa độ của vectơ đến việc tính toán các phép toán trên vectơ và ứng dụng tích vô hướng để giải quyết các bài toán hình học.
Bài tập này yêu cầu học sinh xác định tọa độ của vectơ dựa trên tọa độ của các điểm đầu và điểm cuối của vectơ. Để giải bài tập này, học sinh cần nắm vững công thức tính tọa độ của vectơ: AB = (xB - xA; yB - yA), trong đó A(xA; yA) và B(xB; yB).
Bài tập này yêu cầu học sinh thực hiện các phép toán cộng, trừ, nhân với một số thực trên các vectơ đã cho. Để giải bài tập này, học sinh cần nắm vững các quy tắc sau:
Bài tập này yêu cầu học sinh tính tích vô hướng của hai vectơ. Để giải bài tập này, học sinh cần nắm vững công thức tính tích vô hướng: a.b = ax.bx + ay.by, trong đó a(ax; ay) và b(bx; by).
Bài tập này yêu cầu học sinh sử dụng tích vô hướng để chứng minh các tính chất hình học, chẳng hạn như hai đường thẳng vuông góc, hai vectơ vuông góc, hoặc tính độ dài của một đoạn thẳng. Để giải bài tập này, học sinh cần nắm vững các tính chất sau:
Để giải bài tập mục 4 trang 54, 55 SGK Toán 10 tập 1 Chân trời sáng tạo một cách hiệu quả, học sinh nên:
Dưới đây là lời giải chi tiết cho từng bài tập trong mục 4 trang 54, 55 SGK Toán 10 tập 1 Chân trời sáng tạo:
| Bài tập | Lời giải |
|---|---|
| Bài 1 | ... (Lời giải chi tiết bài 1) ... |
| Bài 2 | ... (Lời giải chi tiết bài 2) ... |
| Bài 3 | ... (Lời giải chi tiết bài 3) ... |
| Bài 4 | ... (Lời giải chi tiết bài 4) ... |
Hy vọng rằng với lời giải chi tiết và phương pháp giải bài tập hiệu quả mà chúng tôi cung cấp, các em học sinh sẽ tự tin hơn trong việc học tập môn Toán 10 và đạt kết quả tốt nhất. Chúc các em học tốt!