Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 tập 1 của giaitoan.edu.vn. Trong bài viết này, chúng ta sẽ cùng nhau đi sâu vào giải chi tiết các bài tập trong mục 2 trang 62 và 63 sách giáo khoa Toán 10 tập 1, chương trình Chân trời sáng tạo.
Giaitoan.edu.vn cung cấp lời giải đầy đủ, dễ hiểu, giúp các em nắm vững kiến thức và rèn luyện kỹ năng giải toán hiệu quả. Hãy cùng bắt đầu nhé!
Trên nửa đường tròn đơn vị, cho dây cung NM song song với trục Ox (Hình 4). Tính tổng số đo của hai góc xOM và xON Tính các giá trị lượng giác: sin120, cos150;cot 135
Tính các giá trị lượng giác: \(\sin {120^o};\cos {150^o};\cot {135^o}.\)
Phương pháp giải:
\(\begin{array}{l}\sin {120^o} = \sin \;({180^o} - {60^o});\\\cos {150^o} = - \cos \;({180^o} - {30^o});\\\cot {135^o} = - \cot \;({180^o} - {45^o}).\end{array}\)
Lời giải chi tiết:
\(\begin{array}{l}\sin {120^o} = \sin \;({180^o} - {60^o}) = \sin {60^o} = \frac{{\sqrt 3 }}{2};\\\cos {150^o} = - \cos \;({180^o} - {30^o}) = - \cos {30^o} = - \frac{{\sqrt 3 }}{2};\\\cot {135^o} = - \cot \;({180^o} - {45^o}) = - \cot {45^o} = - 1.\end{array}\)
Cho biết \(\sin \alpha = \frac{1}{2},\) tìm góc \(\alpha \;({0^o} \le \alpha \le {180^o})\) bằng cách vẽ nửa đường tròn đơn vị.
Phương pháp giải:
Vẽ nửa đường tròn đơn vị.
\(\sin \alpha = \frac{1}{2}\) nên lấy các điểm có tung độ là \(\frac{1}{2}\). Từ đó tính góc \(\alpha \).
Lời giải chi tiết:
Gọi M là điểm thuộc nửa đường tròn đơn vị sao cho: \(\widehat {xOM} = \alpha \)
Do \(\sin \alpha = \frac{1}{2}\) nên tung độ của M bằng \(\frac{1}{2}.\)
Vậy ta xác định được hai điểm N và M thỏa mãn \(\sin \widehat {xON} = \sin \widehat {xOM} = \frac{1}{2}\)
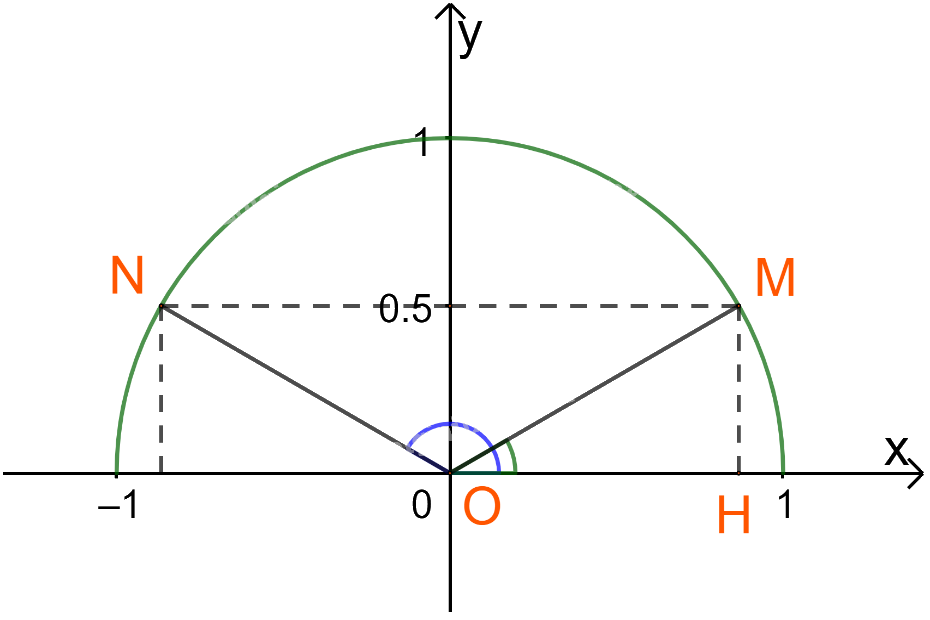
Đặt \(\beta = \widehat {xOM} \Rightarrow \widehat {xON} = {180^o} - \beta \)
Xét tam giác OHM vuông tại H ta có: \(MH = \frac{1}{2} = \frac{{OM}}{2} \Rightarrow \beta = {30^o}\)
\( \Rightarrow \widehat {xON} = {180^o} - {30^o} = {150^o}\)
Vậy \(\alpha = {30^o}\) hoặc \(\alpha = {150^o}\)
Trên nửa đường tròn đơn vị, cho dây cung NM song song với trục Ox (Hình 4). Tính tổng số đo của hai góc \(\widehat {xOM}\) và \(\widehat {xON}.\)

Phương pháp giải:
Tính góc \(\widehat {xON}\) theo góc \(\widehat {xOM}.\)
Lời giải chi tiết:
Gọi H là hình chiếu vuông góc của N Ox.
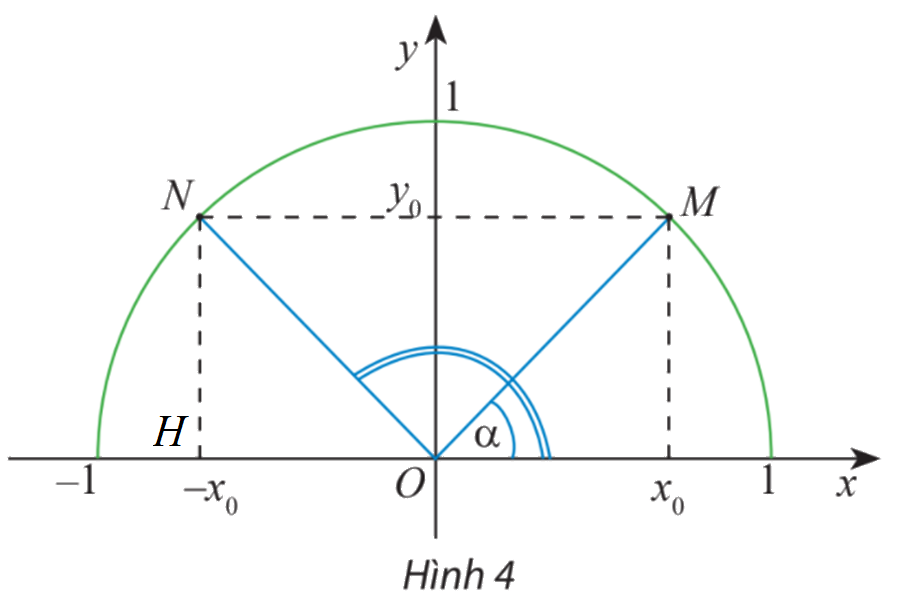
Ta có: \(\widehat {NOH} = \widehat {ONM} = \widehat {OMN} = \widehat {MOx} = \alpha \) (do NM song song với Ox)
Mà \(\widehat {xOM} + \widehat {NOH} = {180^o}\)
Suy ra \(\widehat {xON} + \widehat {MOx} = {180^o}\)
Trên nửa đường tròn đơn vị, cho dây cung NM song song với trục Ox (Hình 4). Tính tổng số đo của hai góc \(\widehat {xOM}\) và \(\widehat {xON}.\)

Phương pháp giải:
Tính góc \(\widehat {xON}\) theo góc \(\widehat {xOM}.\)
Lời giải chi tiết:
Gọi H là hình chiếu vuông góc của N Ox.
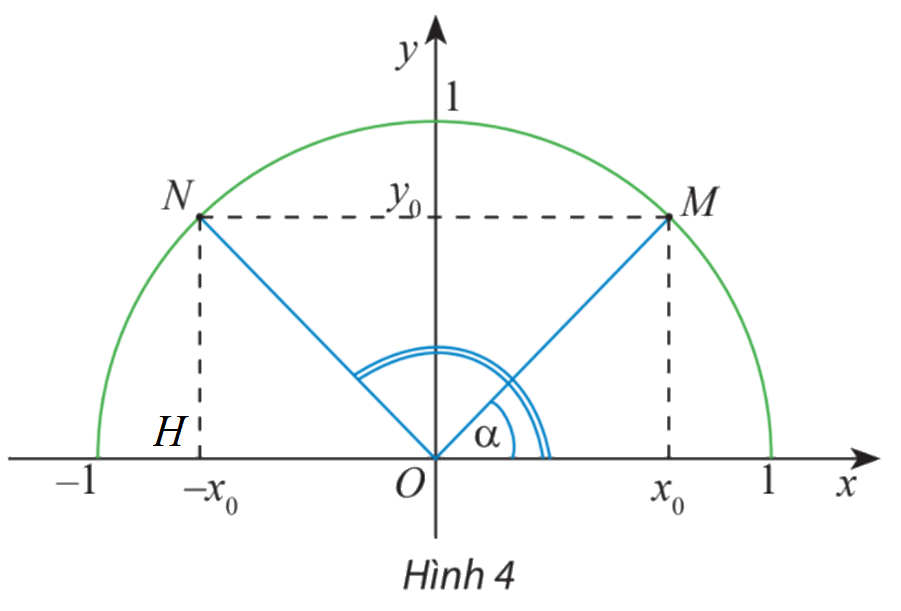
Ta có: \(\widehat {NOH} = \widehat {ONM} = \widehat {OMN} = \widehat {MOx} = \alpha \) (do NM song song với Ox)
Mà \(\widehat {xOM} + \widehat {NOH} = {180^o}\)
Suy ra \(\widehat {xON} + \widehat {MOx} = {180^o}\)
Tính các giá trị lượng giác: \(\sin {120^o};\cos {150^o};\cot {135^o}.\)
Phương pháp giải:
\(\begin{array}{l}\sin {120^o} = \sin \;({180^o} - {60^o});\\\cos {150^o} = - \cos \;({180^o} - {30^o});\\\cot {135^o} = - \cot \;({180^o} - {45^o}).\end{array}\)
Lời giải chi tiết:
\(\begin{array}{l}\sin {120^o} = \sin \;({180^o} - {60^o}) = \sin {60^o} = \frac{{\sqrt 3 }}{2};\\\cos {150^o} = - \cos \;({180^o} - {30^o}) = - \cos {30^o} = - \frac{{\sqrt 3 }}{2};\\\cot {135^o} = - \cot \;({180^o} - {45^o}) = - \cot {45^o} = - 1.\end{array}\)
Cho biết \(\sin \alpha = \frac{1}{2},\) tìm góc \(\alpha \;({0^o} \le \alpha \le {180^o})\) bằng cách vẽ nửa đường tròn đơn vị.
Phương pháp giải:
Vẽ nửa đường tròn đơn vị.
\(\sin \alpha = \frac{1}{2}\) nên lấy các điểm có tung độ là \(\frac{1}{2}\). Từ đó tính góc \(\alpha \).
Lời giải chi tiết:
Gọi M là điểm thuộc nửa đường tròn đơn vị sao cho: \(\widehat {xOM} = \alpha \)
Do \(\sin \alpha = \frac{1}{2}\) nên tung độ của M bằng \(\frac{1}{2}.\)
Vậy ta xác định được hai điểm N và M thỏa mãn \(\sin \widehat {xON} = \sin \widehat {xOM} = \frac{1}{2}\)
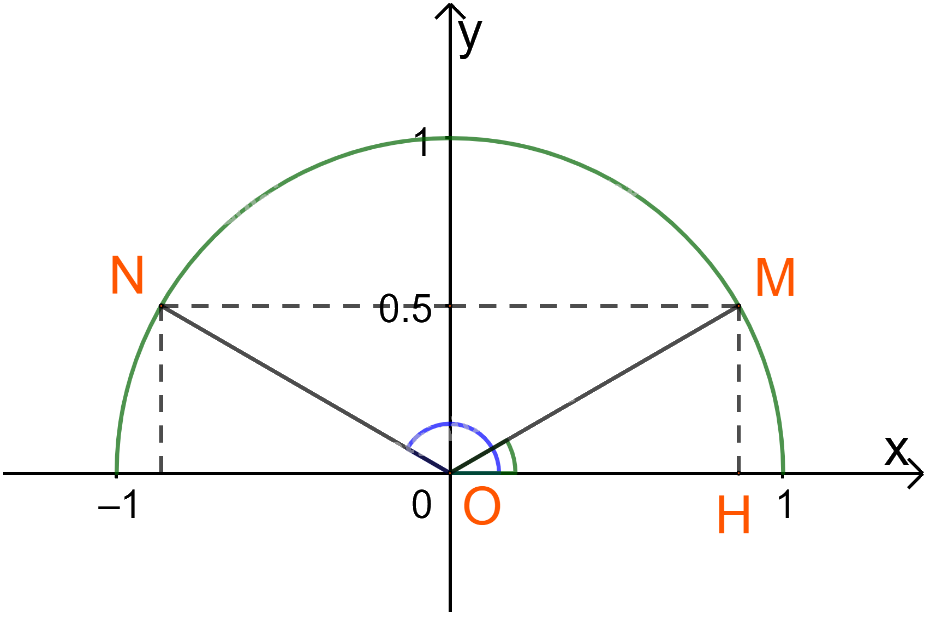
Đặt \(\beta = \widehat {xOM} \Rightarrow \widehat {xON} = {180^o} - \beta \)
Xét tam giác OHM vuông tại H ta có: \(MH = \frac{1}{2} = \frac{{OM}}{2} \Rightarrow \beta = {30^o}\)
\( \Rightarrow \widehat {xON} = {180^o} - {30^o} = {150^o}\)
Vậy \(\alpha = {30^o}\) hoặc \(\alpha = {150^o}\)
Mục 2 của chương trình Toán 10 tập 1, Chân trời sáng tạo tập trung vào các khái niệm cơ bản về tập hợp, các phép toán trên tập hợp, và các tính chất của chúng. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương trình Toán học ở các lớp trên. Bài viết này sẽ cung cấp lời giải chi tiết cho từng bài tập trong mục 2, trang 62 và 63, giúp các em hiểu rõ hơn về các khái niệm và phương pháp giải toán.
Bài tập này yêu cầu các em liệt kê các phần tử của một tập hợp cho trước. Để giải bài tập này, các em cần hiểu rõ định nghĩa của tập hợp và cách xác định các phần tử thuộc tập hợp đó. Ví dụ, nếu tập hợp A được định nghĩa là tập hợp các số tự nhiên chẵn nhỏ hơn 10, thì các phần tử của tập hợp A là: {0, 2, 4, 6, 8}.
Bài tập này yêu cầu các em xác định các tập hợp con của một tập hợp cho trước. Để giải bài tập này, các em cần hiểu rõ định nghĩa của tập hợp con. Một tập hợp B được gọi là tập hợp con của tập hợp A nếu mọi phần tử của B đều là phần tử của A. Ví dụ, nếu A = {1, 2, 3} thì B = {1, 2} là tập hợp con của A.
Bài tập này yêu cầu các em thực hiện các phép toán trên tập hợp, như hợp, giao, hiệu, và phần bù. Để giải bài tập này, các em cần hiểu rõ định nghĩa của từng phép toán và cách thực hiện chúng. Ví dụ, hợp của hai tập hợp A và B là tập hợp chứa tất cả các phần tử thuộc A hoặc thuộc B (hoặc cả hai). Ký hiệu: A ∪ B.
Bài tập này yêu cầu các em chứng minh các đẳng thức tập hợp. Để giải bài tập này, các em cần sử dụng các định nghĩa và tính chất của các phép toán trên tập hợp để biến đổi vế trái của đẳng thức thành vế phải (hoặc ngược lại). Ví dụ, để chứng minh A ∪ B = B ∪ A, các em có thể sử dụng tính chất giao hoán của phép hợp.
Ví dụ 1: Cho A = {1, 2, 3, 4} và B = {3, 4, 5, 6}. Tìm A ∪ B.
Lời giải: A ∪ B = {1, 2, 3, 4, 5, 6}.
Ví dụ 2: Cho A = {1, 2, 3} và B = {2, 3, 4}. Tìm A ∩ B.
Lời giải: A ∩ B = {2, 3}.
Để củng cố kiến thức và kỹ năng giải bài tập về tập hợp, các em có thể tự giải thêm các bài tập trong sách giáo khoa và các tài liệu tham khảo khác. Ngoài ra, các em cũng có thể tham gia các diễn đàn, nhóm học tập trực tuyến để trao đổi kinh nghiệm và học hỏi lẫn nhau.
Hy vọng rằng bài viết này đã cung cấp cho các em những kiến thức và kỹ năng cần thiết để giải quyết các bài tập trong mục 2 trang 62, 63 SGK Toán 10 tập 1, chương trình Chân trời sáng tạo. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!