Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10 tập 1 Chân trời sáng tạo. Bài viết này sẽ hướng dẫn bạn giải bài 7 trang 48 một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập môn Toán.
Số 2 đã trải qua một hành trình thú vị và bị biến đổi sau khi đi qua chiếc hộp đen Bác thợ máy đã giải mã hộp đen cho một số x bất kì như sau: Bên trong HỘP ĐEN là một đoạn chương trình được cài đặt sẵn. Ta xem đoạn chương trình này như một hàm số f(x). Hãy viết iểu thức của f(x) để mô tả sự biến đổi đã tác động lên x.
Đề bài
Số 2 đã trải qua một hành trình thú vị và bị biến đổi sau khi đi qua chiếc hộp đen

Bác thợ máy đã giải mã hộp đen cho một số x bất kì như sau:
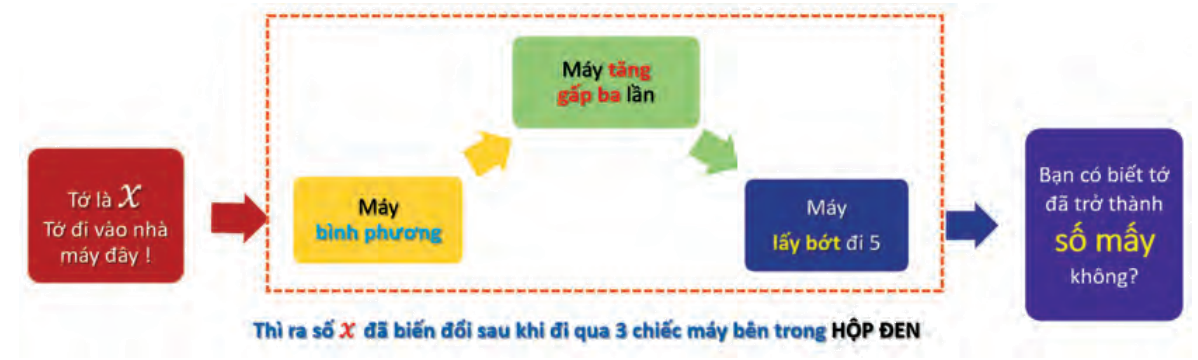
Bên trong HỘP ĐEN là một đoạn chương trình được cài đặt sẵn. Ta xem đoạn chương trình này như một hàm số f(x). Hãy viết iểu thức của f(x) để mô tả sự biến đổi đã tác động lên x.
Lời giải chi tiết
Sau khi vào hộp đen, x đi qua:
+) Đầu tiên, x đi qua hộp màu vàng (bình phương), ta được \({x^2}\)
+) Tiếp tục, \({x^2}\) đi qua hộp màu xanh lá (tăng gấp ba lần), ta được \(3{x^2}\)
+) Cuối cùng, \(3{x^2}\) đi qua hộp màu xanh dương (bớt đi 5), ta được: \(3{x^2} - 5\)
Như vậy sau khi đi qua HỘP ĐEN, số x đã biến đổi thành số \(3{x^2} - 5\)
Kiểm tra lại với số 2: theo công thức thì sau khi qua hộp đen ta được số: \({3.2^2} - 5 = 7\)(đúng).
Vậy biểu thức f(x) mô tả sự biến đổi đã tác động lên x là: \(f(x) = 3{x^2} - 5.\)
Bài 7 trang 48 SGK Toán 10 tập 1 Chân trời sáng tạo thuộc chương 1: Mệnh đề và tập hợp. Bài tập này yêu cầu học sinh vận dụng kiến thức về các phép toán trên tập hợp, bao gồm hợp, giao, hiệu và phần bù của tập hợp để giải quyết các bài toán cụ thể. Việc nắm vững các khái niệm và quy tắc này là nền tảng quan trọng để học tốt các chương tiếp theo của môn Toán 10.
Bài 7 trang 48 SGK Toán 10 tập 1 Chân trời sáng tạo thường bao gồm các dạng bài tập sau:
Để giúp bạn hiểu rõ hơn về cách giải bài tập này, chúng tôi sẽ trình bày lời giải chi tiết cho từng phần của bài 7 trang 48 SGK Toán 10 tập 1 Chân trời sáng tạo.
Cho A = {1, 2, 3, 4}, B = {3, 4, 5, 6}. Hãy xác định:
Lời giải:
Chứng minh rằng A ∪ B = B ∪ A với mọi tập hợp A và B.
Lời giải:
Để chứng minh A ∪ B = B ∪ A, ta cần chứng minh rằng mọi phần tử thuộc A ∪ B đều thuộc B ∪ A và ngược lại.
Giả sử x ∈ A ∪ B. Điều này có nghĩa là x ∈ A hoặc x ∈ B. Nếu x ∈ A thì x ∈ B ∪ A. Nếu x ∈ B thì x ∈ B ∪ A. Vậy, x ∈ B ∪ A. Do đó, A ∪ B ⊆ B ∪ A.
Tương tự, nếu x ∈ B ∪ A thì x ∈ B hoặc x ∈ A. Nếu x ∈ B thì x ∈ A ∪ B. Nếu x ∈ A thì x ∈ A ∪ B. Vậy, x ∈ A ∪ B. Do đó, B ∪ A ⊆ A ∪ B.
Từ A ∪ B ⊆ B ∪ A và B ∪ A ⊆ A ∪ B, ta suy ra A ∪ B = B ∪ A.
Để củng cố kiến thức, bạn có thể làm thêm các bài tập tương tự sau:
Bài 7 trang 48 SGK Toán 10 tập 1 Chân trời sáng tạo là một bài tập quan trọng giúp bạn làm quen với các khái niệm và phép toán cơ bản về tập hợp. Hy vọng rằng với lời giải chi tiết và các mẹo giải bài tập mà chúng tôi đã cung cấp, bạn sẽ tự tin hơn trong quá trình học tập môn Toán 10.