Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10 tập 1 Chân trời sáng tạo. Bài viết này sẽ giúp bạn nắm vững kiến thức và kỹ năng giải bài 8 trang 73 một cách hiệu quả.
Chúng tôi cam kết mang đến cho bạn trải nghiệm học toán online tốt nhất với đội ngũ giáo viên giàu kinh nghiệm và phương pháp giảng dạy tiên tiến.
Cho ha là đường cao vẽ từ đỉnh A, R là bán kính đường tròn ngoại tiếp tam giác ABC. Chứng minh hệ thức: ha= 2Rsin Bsin C.
Đề bài
Cho \({h_a}\) là đường cao vẽ từ đỉnh A, R là bán kính đường tròn ngoại tiếp tam giác ABC. Chứng minh hệ thức: \({h_a} = 2R\sin B\sin C.\)
Phương pháp giải - Xem chi tiết
Bước 1: Tính \({h_a}\) theo b và sinC
Bước 2: Tính b theo R và sinB. Từ đó suy ra điều phải chứng minh.
Lời giải chi tiết
Đặt \(a = BC,b = AC,c = AB\)
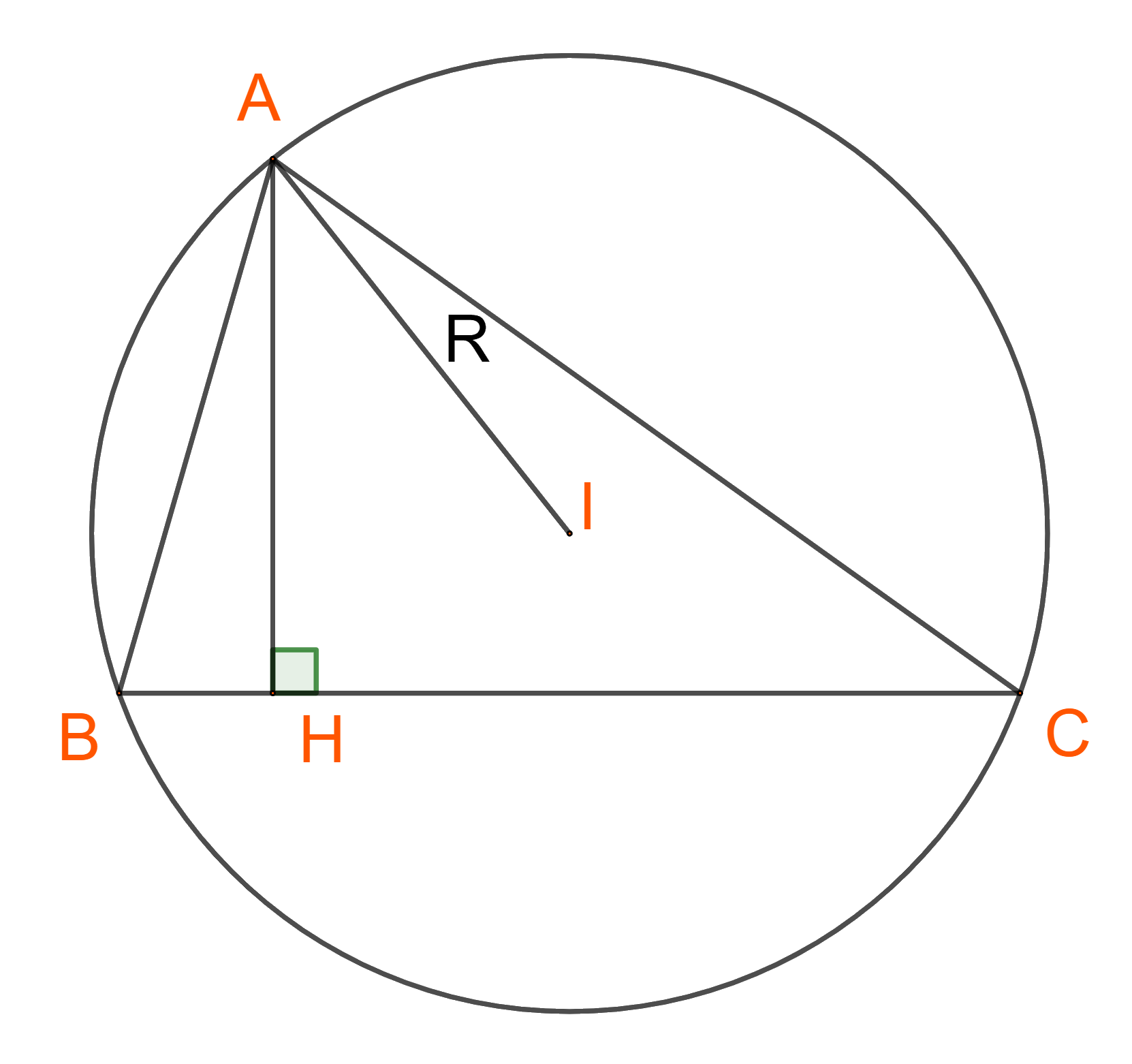
Ta có: \(\sin C = \frac{{AH}}{{AC}} = \frac{{{h_a}}}{b} \Rightarrow {h_a} = b.\sin C\)
Theo định lí sin, ta có: \(\frac{b}{{\sin B}} = 2R \Rightarrow b = 2R.\sin B\)
\( \Rightarrow {h_a} = 2R.\sin B.\sin C\)
Bài 8 trang 73 SGK Toán 10 tập 1 Chân trời sáng tạo thuộc chương trình học về Vectơ trong mặt phẳng. Bài tập này tập trung vào việc vận dụng các kiến thức về phép cộng, phép trừ vectơ, tích của một số với vectơ, và các tính chất của các phép toán này để giải quyết các bài toán cụ thể.
Bài 8 bao gồm các câu hỏi và bài tập khác nhau, yêu cầu học sinh:
Cho hai vectơ a và b. Tìm vectơ c sao cho a + b = c.
Lời giải:
Vectơ c là tổng của hai vectơ a và b. Để tìm c, ta thực hiện phép cộng vectơ theo quy tắc hình bình hành hoặc quy tắc tam giác.
Cho hai vectơ a và b. Tìm vectơ d sao cho a - b = d.
Lời giải:
Vectơ d là hiệu của hai vectơ a và b. Để tìm d, ta thực hiện phép trừ vectơ bằng cách cộng a với vectơ đối của b.
Ngoài SGK Toán 10 tập 1 Chân trời sáng tạo, bạn có thể tham khảo thêm các tài liệu sau:
Bài 8 trang 73 SGK Toán 10 tập 1 Chân trời sáng tạo là một bài tập quan trọng giúp bạn củng cố kiến thức về vectơ. Hy vọng với lời giải chi tiết và các mẹo giải bài tập hiệu quả mà giaitoan.edu.vn cung cấp, bạn sẽ tự tin hơn trong việc học tập môn Toán.