Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2 trang 65, 66, 67 sách giáo khoa Toán 10 tập 2 - Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong học tập.
Lấy một cây thước thẳng với mép thước AB có chiều dài d và một đoạn dây không đàn hồi có chiều dài Viết phương trình chính tắc của hypebol có tiêu cự bằng 10 và độ dài trục nhỏ bằng 6. Một tháp làm nguội của một nhà cát có mặt cắt là một hypebol có phương trình
Viết phương trình chính tắc của hypebol có tiêu cự bằng 10 và độ dài trục nhỏ bằng 6.
Phương pháp giải:
Phương trình chính tắc của hypebol có dạng \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) với \(M(x;y) \in (H);b = \sqrt {{c^2} - {a^2}} \)
Lời giải chi tiết:
Ta có: \(2c = 10 \Rightarrow c = 5,2b = 6 \Rightarrow b = 3\)
Suy ra \(a = \sqrt {{c^2} - {b^2}} = \sqrt {{5^2} - {3^2}} = 4\)
Vậy phương trình chính tắc của hypebol có dạng \(\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{9} = 1\)
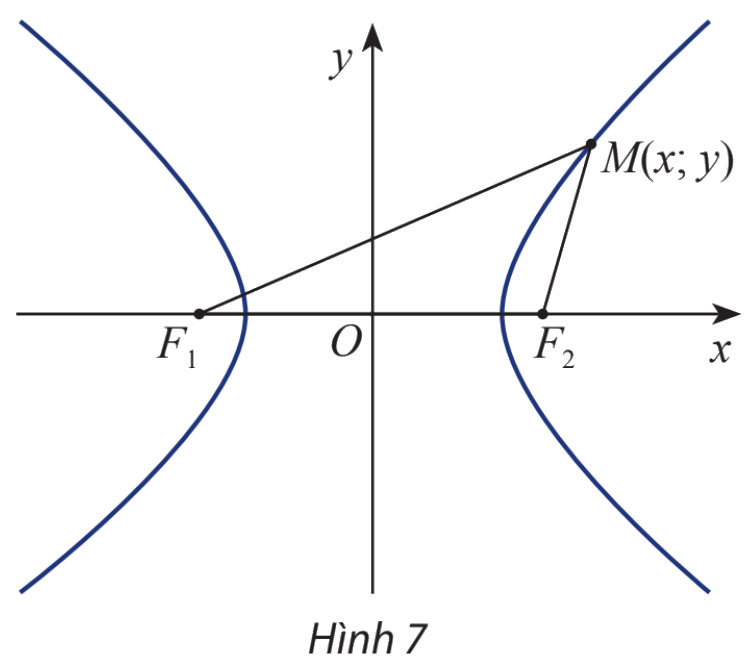
Cho hyperbol (H) có các tiêu điểm \({F_1}\) và \({F_2}\) và đặt điểm \({F_1}{F_2} = 2c\). Chọn hệ trục tọa độ Oxy sao cho \({F_1}( - c;0)\) và \({F_2}(c;0)\)
Xét điểm \(M(x;y)\)
a) Tính \({F_1}M\) và \({F_2}M\) theo x, y và c
b) Giải thích phát biểu sau:
\(M(x;y) \in (H) \Leftrightarrow \left| {\sqrt {{{\left( {x + c} \right)}^2} + {y^2}} - \sqrt {{{\left( {x - c} \right)}^2} + {y^2}} } \right| = 2a\)
Phương pháp giải:
Sử dụng phương pháp tọa độ trong mặt phẳng
Lời giải chi tiết:
a) Ta có:
\(\overrightarrow {{F_1}M} = \left( {x + c;y} \right) \Rightarrow {F_1}M = \sqrt {{{\left( {x + c} \right)}^2} + {y^2}} \)
\(\overrightarrow {{F_2}M} = \left( {x - c;y} \right) \Rightarrow {F_2}M = \sqrt {{{\left( {x - c} \right)}^2} + {y^2}} \)
b) Ta có \(M(x;y) \in (E)\) nên \(\left| {{F_1}M - {F_2}M} \right| = 2a \Leftrightarrow \left| {\sqrt {{{\left( {x + c} \right)}^2} + {y^2}} - \sqrt {{{\left( {x - c} \right)}^2} + {y^2}} } \right| = 2a\)
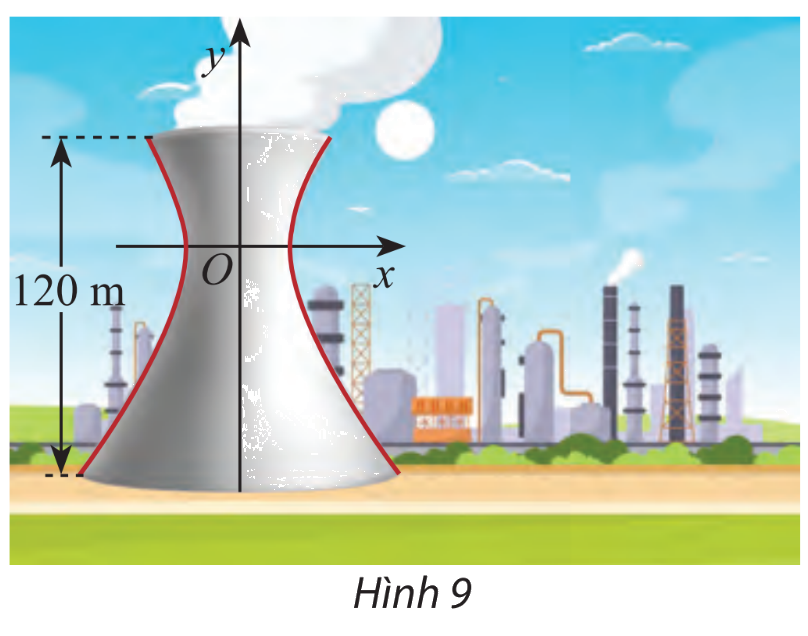
Một tháp làm nguội của một nhà cát có mặt cắt là một hypebol có phương trình \(\frac{{{x^2}}}{{{{27}^2}}} - \frac{{{y^2}}}{{{{40}^2}}} = 1\) (hình 9). Cho biết chiều cao của tháp là 120 m và khoảng cách từ nóc tháp đến tâm đối xứng của hypebol bằng một nửa khoảng cách từ tâm đối xứng đến đáy. Tìm bán kính đường tròn nóc và bán kính đường tròn đáy của tháp.
Phương pháp giải:
Bước 1: Xác định khoảng cách từ tâm đến đỉnh tháp và đáy tháp
Bước 2: Từ kết quả vừa tìm thay vào phương trình hypebol y bằng kết quả đó tìm x (Chỉ lấy kết quả dương)
Lời giải chi tiết:
Gọi khoảng cách từ tâm đối xứng đến đỉnh tháp là z
Suy ra khoảng cách từ tâm đối xứng đến đáy tháp là 2z
Ta có \(z + 2z = 120 \Rightarrow z = 40\)
Thay \(y = 40\) vào phương trình \(\frac{{{x^2}}}{{{{27}^2}}} - \frac{{{y^2}}}{{{{40}^2}}} = 1\) ta tìm được \(x = 27\sqrt 2 \)
Thay \(y = 80\) vào phương trình \(\frac{{{x^2}}}{{{{27}^2}}} - \frac{{{y^2}}}{{{{40}^2}}} = 1\) ta tìm được \(x = 27\sqrt 5 \)
Vậy bán kính đường tròn nóc và bán kính đường tròn đáy của tháp lần lượt là \(27\sqrt 2 \) và \(27\sqrt 5 \)
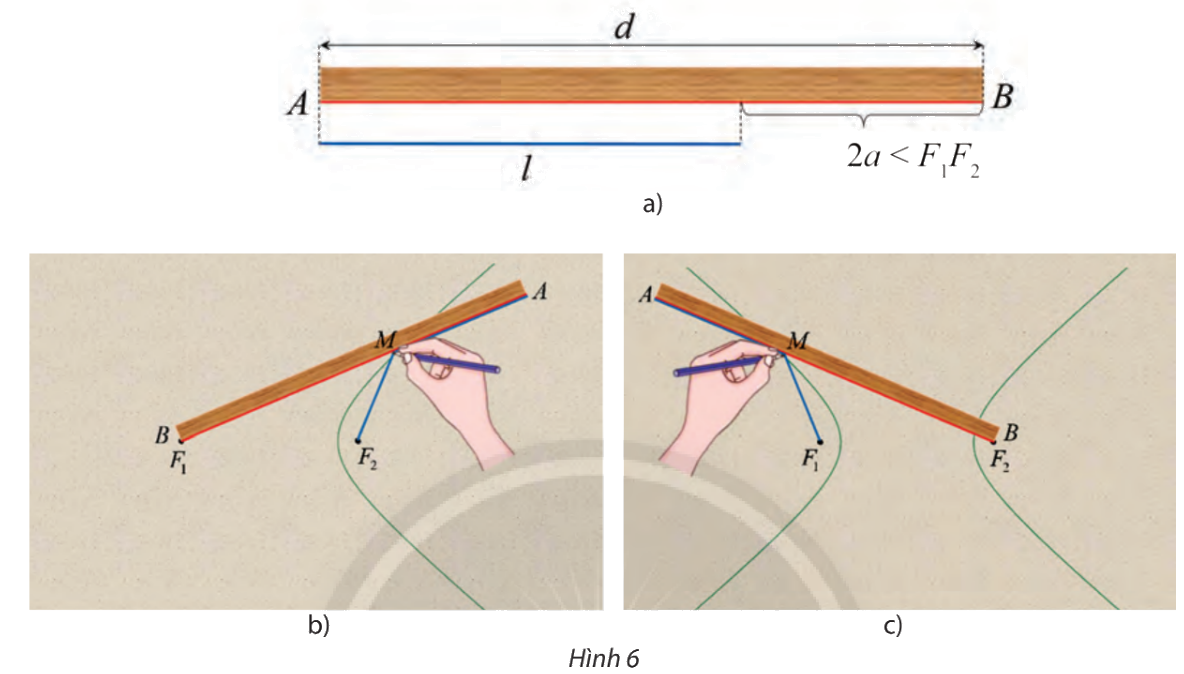
Lấy một tấm bìa, trên đó đánh dấu hai điểm \({F_1}\) và \({F_2}\). Lấy một cây thước thẳng với mép thước AB có chiều dài d và một đoạn dây không đàn hồi có chiều dài l sao cho \(d - l = 2a\) nhỏ hơn khoảng cách \({F_1}{F_2}\) (hình 6a).
Đính một đầu dây vào đầu A của thước, dùng đinh ghim đầu dây còn lại vào điểm \({F_2}\). Đặt thước sao cho đầu B của thước trùng với điểm \({F_1}\). Tựa đầu bút chì vào dây, di chuyển điểm M trên tấm bìa và giữ sao cho dây luôn căng, đoạn AM ép sát vào thước, khi đó M sẽ gạch lên tấm bìa một đường (H) (xem hình 6b)
a) Chứng tỏ rằng khi M di động, ta luôn có \(M{F_1} - M{F_2} = 2a\)
b) Vẫn đính một đầu dây vào đầu A của thước nhưng đổi chỗ cố định đầu dây còn lại vào \({F_1}\), đầu B của thước trùng với \({F_2}\) sao cho đoạn thẳng BA có thể quay quanh \({F_2}\)và làm tương tự như lần đầu để bút chì M vẽ được một nhánh khác của đường (H) (hình 6c). Tính \(M{F_2} - M{F_1}\)
Lời giải chi tiết:
a) Khi điểm M trùng với điểm A ta có:
\(M{F_1} - M{F_2} = A{F_1} - A{F_2} = AB - A{F_2} = d - l = 2a\)
b) Tương tự khi điểm M trùng với điểm A ta có:
\(M{F_2} - M{F_1} = A{F_2} - A{F_1} = AB - A{F_1} = d - l = 2a\)
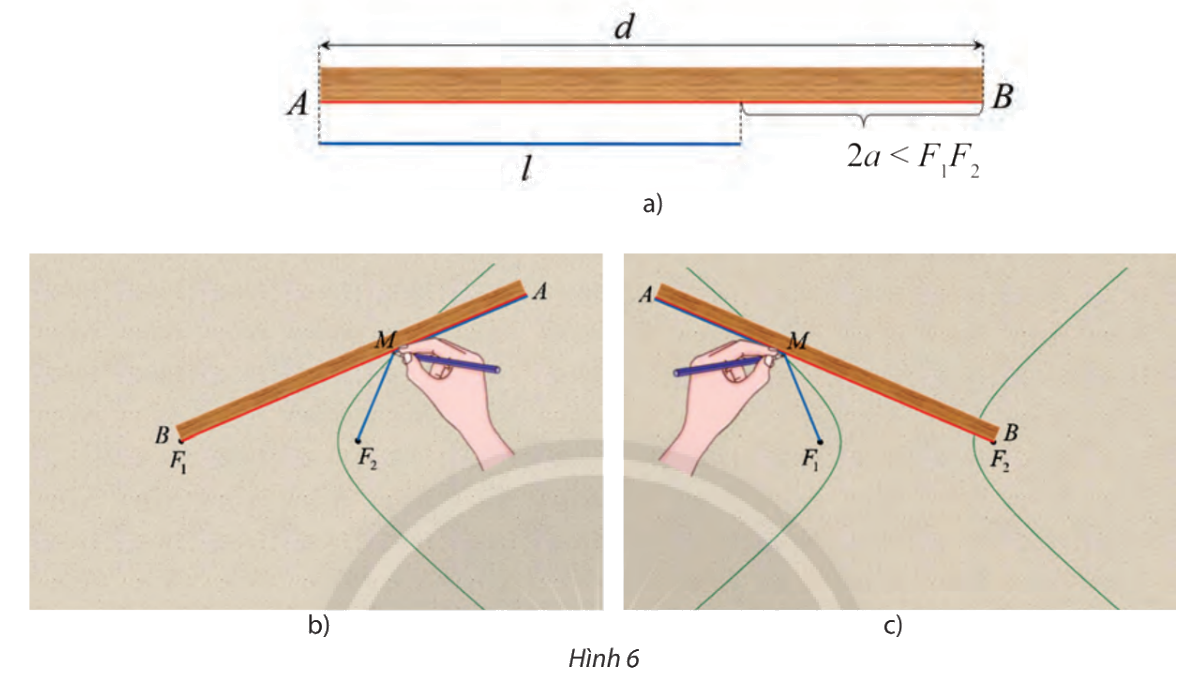
Lấy một tấm bìa, trên đó đánh dấu hai điểm \({F_1}\) và \({F_2}\). Lấy một cây thước thẳng với mép thước AB có chiều dài d và một đoạn dây không đàn hồi có chiều dài l sao cho \(d - l = 2a\) nhỏ hơn khoảng cách \({F_1}{F_2}\) (hình 6a).
Đính một đầu dây vào đầu A của thước, dùng đinh ghim đầu dây còn lại vào điểm \({F_2}\). Đặt thước sao cho đầu B của thước trùng với điểm \({F_1}\). Tựa đầu bút chì vào dây, di chuyển điểm M trên tấm bìa và giữ sao cho dây luôn căng, đoạn AM ép sát vào thước, khi đó M sẽ gạch lên tấm bìa một đường (H) (xem hình 6b)
a) Chứng tỏ rằng khi M di động, ta luôn có \(M{F_1} - M{F_2} = 2a\)
b) Vẫn đính một đầu dây vào đầu A của thước nhưng đổi chỗ cố định đầu dây còn lại vào \({F_1}\), đầu B của thước trùng với \({F_2}\) sao cho đoạn thẳng BA có thể quay quanh \({F_2}\)và làm tương tự như lần đầu để bút chì M vẽ được một nhánh khác của đường (H) (hình 6c). Tính \(M{F_2} - M{F_1}\)
Lời giải chi tiết:
a) Khi điểm M trùng với điểm A ta có:
\(M{F_1} - M{F_2} = A{F_1} - A{F_2} = AB - A{F_2} = d - l = 2a\)
b) Tương tự khi điểm M trùng với điểm A ta có:
\(M{F_2} - M{F_1} = A{F_2} - A{F_1} = AB - A{F_1} = d - l = 2a\)
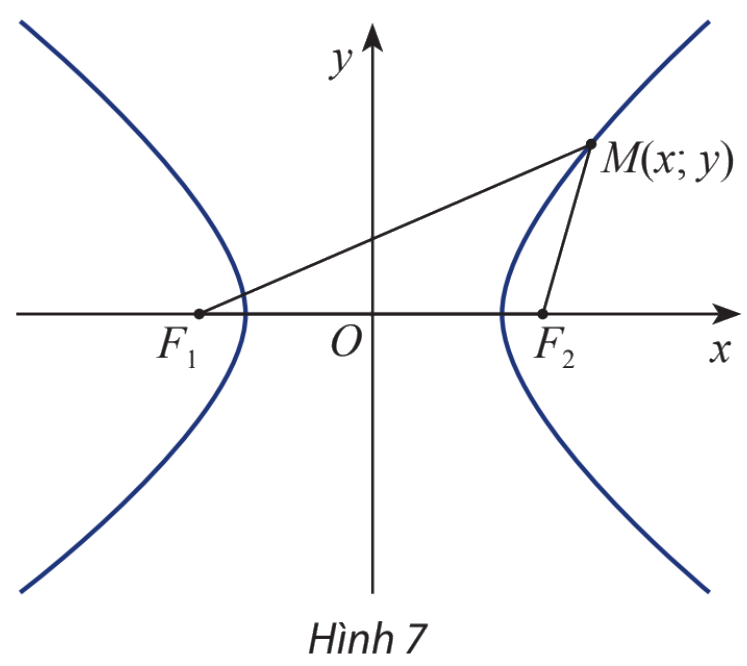
Cho hyperbol (H) có các tiêu điểm \({F_1}\) và \({F_2}\) và đặt điểm \({F_1}{F_2} = 2c\). Chọn hệ trục tọa độ Oxy sao cho \({F_1}( - c;0)\) và \({F_2}(c;0)\)
Xét điểm \(M(x;y)\)
a) Tính \({F_1}M\) và \({F_2}M\) theo x, y và c
b) Giải thích phát biểu sau:
\(M(x;y) \in (H) \Leftrightarrow \left| {\sqrt {{{\left( {x + c} \right)}^2} + {y^2}} - \sqrt {{{\left( {x - c} \right)}^2} + {y^2}} } \right| = 2a\)
Phương pháp giải:
Sử dụng phương pháp tọa độ trong mặt phẳng
Lời giải chi tiết:
a) Ta có:
\(\overrightarrow {{F_1}M} = \left( {x + c;y} \right) \Rightarrow {F_1}M = \sqrt {{{\left( {x + c} \right)}^2} + {y^2}} \)
\(\overrightarrow {{F_2}M} = \left( {x - c;y} \right) \Rightarrow {F_2}M = \sqrt {{{\left( {x - c} \right)}^2} + {y^2}} \)
b) Ta có \(M(x;y) \in (E)\) nên \(\left| {{F_1}M - {F_2}M} \right| = 2a \Leftrightarrow \left| {\sqrt {{{\left( {x + c} \right)}^2} + {y^2}} - \sqrt {{{\left( {x - c} \right)}^2} + {y^2}} } \right| = 2a\)
Viết phương trình chính tắc của hypebol có tiêu cự bằng 10 và độ dài trục nhỏ bằng 6.
Phương pháp giải:
Phương trình chính tắc của hypebol có dạng \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) với \(M(x;y) \in (H);b = \sqrt {{c^2} - {a^2}} \)
Lời giải chi tiết:
Ta có: \(2c = 10 \Rightarrow c = 5,2b = 6 \Rightarrow b = 3\)
Suy ra \(a = \sqrt {{c^2} - {b^2}} = \sqrt {{5^2} - {3^2}} = 4\)
Vậy phương trình chính tắc của hypebol có dạng \(\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{9} = 1\)
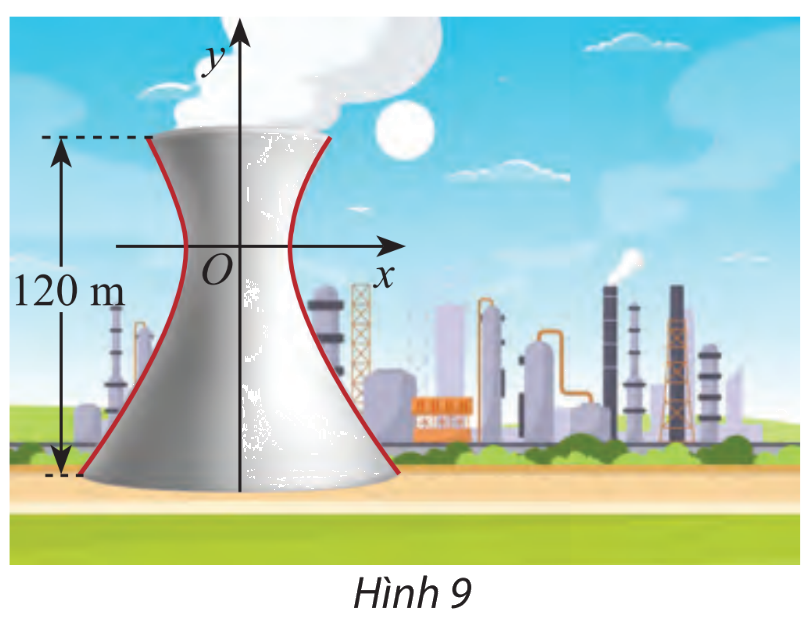
Một tháp làm nguội của một nhà cát có mặt cắt là một hypebol có phương trình \(\frac{{{x^2}}}{{{{27}^2}}} - \frac{{{y^2}}}{{{{40}^2}}} = 1\) (hình 9). Cho biết chiều cao của tháp là 120 m và khoảng cách từ nóc tháp đến tâm đối xứng của hypebol bằng một nửa khoảng cách từ tâm đối xứng đến đáy. Tìm bán kính đường tròn nóc và bán kính đường tròn đáy của tháp.
Phương pháp giải:
Bước 1: Xác định khoảng cách từ tâm đến đỉnh tháp và đáy tháp
Bước 2: Từ kết quả vừa tìm thay vào phương trình hypebol y bằng kết quả đó tìm x (Chỉ lấy kết quả dương)
Lời giải chi tiết:
Gọi khoảng cách từ tâm đối xứng đến đỉnh tháp là z
Suy ra khoảng cách từ tâm đối xứng đến đáy tháp là 2z
Ta có \(z + 2z = 120 \Rightarrow z = 40\)
Thay \(y = 40\) vào phương trình \(\frac{{{x^2}}}{{{{27}^2}}} - \frac{{{y^2}}}{{{{40}^2}}} = 1\) ta tìm được \(x = 27\sqrt 2 \)
Thay \(y = 80\) vào phương trình \(\frac{{{x^2}}}{{{{27}^2}}} - \frac{{{y^2}}}{{{{40}^2}}} = 1\) ta tìm được \(x = 27\sqrt 5 \)
Vậy bán kính đường tròn nóc và bán kính đường tròn đáy của tháp lần lượt là \(27\sqrt 2 \) và \(27\sqrt 5 \)
Mục 2 của chương trình Toán 10 tập 2 - Chân trời sáng tạo tập trung vào việc nghiên cứu về vectơ. Các em sẽ được làm quen với các khái niệm cơ bản như vectơ, phép cộng, phép trừ vectơ, tích của một số với vectơ, và ứng dụng của vectơ trong hình học.
Trang 65 tập trung vào các bài tập về khái niệm vectơ, cách xác định vectơ, và các tính chất cơ bản của vectơ. Các bài tập thường yêu cầu học sinh:
Trang 66 đi sâu hơn vào các phép toán trên vectơ, bao gồm phép cộng, phép trừ vectơ, và tích của một số với vectơ. Các bài tập thường yêu cầu học sinh:
Trang 67 tập trung vào ứng dụng của vectơ trong hình học, đặc biệt là trong việc chứng minh các tính chất của hình bình hành, hình thang, và các hình đặc biệt khác. Các bài tập thường yêu cầu học sinh:
Bài tập: Cho tam giác ABC. Gọi M là trung điểm của BC. Chứng minh rằng AB + AC = 2AM.
Lời giải:
Ta có: AB + AC = AB + (AB + BC) = 2AB + BC. Vì M là trung điểm của BC nên BC = 2BM. Do đó, 2AB + BC = 2AB + 2BM = 2(AB + BM) = 2AM. Vậy AB + AC = 2AM (đpcm).
Để học tốt môn Toán, đặc biệt là phần vectơ, các em cần:
Hy vọng với những hướng dẫn chi tiết và ví dụ minh họa trên, các em sẽ tự tin hơn trong việc giải các bài tập mục 2 trang 65, 66, 67 SGK Toán 10 tập 2 - Chân trời sáng tạo. Chúc các em học tập tốt!