Chào mừng bạn đến với bài học về Lý thuyết Xác suất của biến cố, một phần quan trọng trong chương trình SGK Toán 10 Chân trời sáng tạo. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản nhất về xác suất, giúp bạn hiểu rõ hơn về thế giới xung quanh.
Chúng tôi tại giaitoan.edu.vn cam kết mang đến cho bạn những bài giảng chất lượng, dễ hiểu và bài tập thực hành phong phú để bạn có thể tự tin chinh phục môn Toán.
A. Lý thuyết 1. Xác suất của biến cố
A. Lý thuyết
1. Xác suất của biến cố
Giả sử một phép thử có không gian mẫu Ω gồm hữu hạn các kết quả có cùng khả năng xảy ra là một biến cố. Xác suất của biến cố A là một số, kí hiệu là P(A), được xác định bởi công thức: \(\frac{{n(A)}}{{n(\Omega )}}\) trong đó n(A), n(Ω) lần lượt kí hiệu số phần tử của tập hợp A và Ω. |
Chú ý:
- Định nghĩa trên được gọi là định nghĩa cổ điển của xác suất.
- Với mọi biến cố A, \(0 \le P(A) \le 1\).
- \(P(\emptyset ) = 0\); \(P(\Omega ) = 1\).
2. Tính xác suất bằng sơ đồ hình cây
Trong chương VIII, chúng ta đã được làm quen với phương pháp sử dụng sơ đồ hình cây để liệt kê các kết quả của một thí nghiệm. Ta cũng có thể sử dụng sơ đồ hình cây để tính xác suất.
3. Biến cố đối
Cho A là một biến cố. Khi đó, biến cố “Không xảy ra A”, kí hiệu là \(\overline A \), được gọi là biến cố đối của A. + \(\overline A = \Omega \backslash A\). + \(P(\overline A ) + P(A) = 1\). |
4. Nguyên lí xác suất bé
Nếu một biến cố có xác suất rất bé thì trong một phép thử, biến cố đó sẽ không xảy ra.
Tuy nhiên, một xác suất như thế nào được xem là bé phụ thuộc vào từng bài toán cụ thể.
B. Bài tập
Bài 1: Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên đồng thời 2 chiếc thẻ từ trong hộp.
a) Gọi Ω là không gian mẫu trong trò chơi trên. Tính số phần tử của tập hợp Ω.
b) Tính xác suất của biến cố E: “Tổng các số trên hai thẻ là số lẻ”.
Giải:
a) Mỗi phần tử của không gian mẫu Ω là một tổ hợp chập 2 của 5 phần tử trong tập hợp {1;2;3;4;5}. Vì thế \(n(\Omega ) = C_5^2 = \frac{{5!}}{{2!.3!}} = \frac{{5.4}}{2} = 10\).
b) Biến cố E gồm các cách chọn ra hai chiếc thẻ ghi số là: 1 và 2; 1 và 4; 2 và 3; 2 và 5; 3 và 4; 4 và 5. Vì thế n(E) = 6. Vậy xác suất của biến cố E là:
\(P(E) = \frac{{n(E)}}{{n(\Omega )}} = \frac{6}{{10}} = \frac{3}{5}\).
Bài 2: Nhân dịp khai trương một cửa hàng kinh doanh đồ điện tử, khách hàng đầu tiên sau khi mua hàng sẽ được nhận một phiếu tặng quà. Món quà là một chiếc tai nghe của một trong năm hãng và tai nghe mỗi hãng có hai màu trắng hoặc đen.
a) Vẽ sơ đồ hình cây biểu thị các khả năng của một món quà mà khách hàng đầu tiên có thể nhận được từ phiếu tặng quà.
b) Tính xác suất của biến cố H: “Khách hàng đầu tiên nhận được chiếc tai nghe màu trắng từ phiếu tặng quà”.
Giải:
a) Sơ đồ hình cây biểu thị các khả năng của một món quà mà khách hàng đầu tiên có thể nhận được từ phiếu tặng quà:
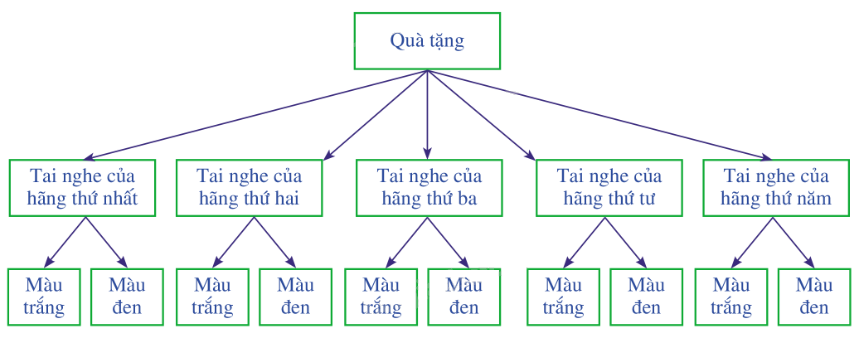
b) Ta thấy không gian mẫu Ω là các loại tai nghe đếm theo hãng và theo màu của tai nghe. Dựa vào sơ đồ hình cây ở trên, ta thấy:
+ n(Ω) = 10.
+ Khách hàng đầu tiên có thể nhận được 1 trong 5 loại tai nghe màu trắng ứng với hãng, tức là n(H) = 5.
Vậy xác suất xảy ra biến cố H là \(P(H) = \frac{{n(H)}}{{n(\Omega )}} = \frac{5}{{10}} = \frac{1}{2}\).
Bài 3: Một hộp có 10 quả bóng trắng và 10 quả bóng đỏ; các quả bóng có kích thước và khối lượng giống nhau. Lấy ngẫu nhiên đồng thời 9 quả bóng trong hộp. Tính xác suất để trong 9 quả bóng được lấy ra có ít nhất một quả bóng màu đỏ.
Giải:
Mỗi cách lấy ra đồng thời 9 quả bóng là một tổ hợp chập 9 của 20 phần tử. Do đó, không gian mẫu Ω gồm các tổ hợp chập 9 của 20 phần tử và \(n(\Omega ) = C_{20}^9\).
Xét biến cố K: “Trong 9 quả bóng được lấy ra có ít nhất một quả bóng màu đỏ”.
Khi đó biến cố đối của biến cố K là biến cố \(\overline K \): “Trong 9 quả bóng được lấy ra không có quả bóng màu đỏ nào”, tức là cả 9 quả bóng được lấy ra có màu trắng.
Mỗi cách lấy ra đồng thời 9 quả bóng màu trắng là một tổ hợp chập 9 của 10 phần tử.
Do đó \(n(\overline K ) = C_{10}^9 = \frac{{10!}}{{9!.1!}} = 10\). Suy ra \(P(\overline K ) = \frac{{n(\overline K )}}{{n(\Omega )}} = \frac{{10}}{{C_{20}^9}}\).
Vậy \(P(K) = 1 - P(\overline K ) = 1 - \frac{{10}}{{C_{20}^9}}\).
Bài 4: Trong hộp có 5 viên bi xanh và 7 viên bi trắng có kích thước và khối lượng như nhau. Ta lấy hai viên bi bằng hai cách như sau:
Cách thứ nhất: Lấy ngẫu nhiên một viên bi, xem màu rồi trả lại hộp. Sau đó lại lấy một viên bi một cách ngẫu nhiên.
Cách thứ hai: Lấy cùng một lúc hai viên bi từ hộp.
Gọi A là biến cố “Cả hai lần đều lấy được bi màu trắng”. Với cách lấy bi nào thì biến cố A có khả năng xảy ra cao hơn?
Giải:
Theo cách lấy bi thứ nhất, áp dụng quy tắc nhân ta có số phần tử của không gian mẫu là n(Ω) = 12.12 = 144.
Số khả năng thuận lợi cho A là n(A) = 7.7 = 49.
Do đó xác suất của biến cố A theo cách lấy bi thứ nhất là \(\frac{{49}}{{144}}\).
Theo cách lấy bi thứ hai, số phần tử của không gian mẫu là n(Ω) = \(C_{12}^2\) = 66.
Số khả năng thuận lợi cho A là n(A) = \(C_7^2\) = 21.
Do đó xác suất của biến cố A theo cách lấy bi thứ hai là \(\frac{{21}}{{66}} = \frac{7}{{22}}\).
Vì \(\frac{{49}}{{144}} > \frac{7}{{22}}\) nên với cách lấy bi thứ nhất thì biến cố A có khả năng xảy ra cao hơn.
Xác suất là một lĩnh vực quan trọng của toán học, ứng dụng rộng rãi trong nhiều lĩnh vực của đời sống và khoa học. Việc nắm vững lý thuyết xác suất là nền tảng để giải quyết các bài toán thực tế và hiểu rõ hơn về các hiện tượng ngẫu nhiên.
Trong lý thuyết xác suất, biến cố là một sự kiện có thể xảy ra hoặc không xảy ra trong một thí nghiệm ngẫu nhiên. Không gian mẫu (Ω) là tập hợp tất cả các kết quả có thể xảy ra của thí nghiệm đó.
Nếu không gian mẫu Ω là hữu hạn và các kết quả trong Ω có tính chất đồng khả năng, xác suất của biến cố A được tính bằng công thức:
P(A) = (Số kết quả thuận lợi cho A) / (Tổng số kết quả có thể xảy ra)
Ví dụ: Tính xác suất xuất hiện mặt 6 khi gieo một con xúc xắc sáu mặt.
P(A) = 1 / 6
Có một số phép toán cơ bản trên các biến cố:
Một số quy tắc xác suất quan trọng:
Bài tập 1: Một hộp chứa 5 quả bóng đỏ và 3 quả bóng xanh. Lấy ngẫu nhiên 2 quả bóng từ hộp. Tính xác suất để lấy được 2 quả bóng đỏ.
Bài tập 2: Gieo hai con xúc xắc sáu mặt. Tính xác suất để tổng số chấm trên hai con xúc xắc bằng 7.
Lý thuyết xác suất có ứng dụng rộng rãi trong nhiều lĩnh vực:
Lý thuyết xác suất là một lĩnh vực rộng lớn và phức tạp. Trong chương trình Toán 10, chúng ta chỉ mới tiếp cận với những kiến thức cơ bản nhất. Để hiểu sâu hơn về lý thuyết xác suất, bạn có thể tìm hiểu thêm về các khái niệm như xác suất có điều kiện, biến ngẫu nhiên, phân phối xác suất,...
Hy vọng bài học này đã giúp bạn nắm vững những kiến thức cơ bản về Lý thuyết Xác suất của biến cố trong SGK Toán 10 Chân trời sáng tạo. Chúc bạn học tập tốt!