Hàm số bậc hai là một trong những kiến thức nền tảng và quan trọng của chương trình Toán 10. Việc nắm vững lý thuyết hàm số bậc hai không chỉ giúp học sinh giải quyết các bài tập trong sách giáo khoa mà còn là bước đệm vững chắc cho các kiến thức nâng cao ở các lớp học tiếp theo.
Tại giaitoan.edu.vn, chúng tôi cung cấp tài liệu học tập đầy đủ, chi tiết và dễ hiểu về lý thuyết hàm số bậc hai, giúp bạn tự tin chinh phục môn Toán.
1. Hàm số bậc hai 2. Đồ thị hàm số bậc hai
1. Hàm số bậc hai
+ Định nghĩa:
Hàm số bậc hai biến x là hàm số cho bởi công thức dạng \(y = f(x) = a{x^2} + bx + c\) với \(a,b,c \in \mathbb{R};a \ne 0.\)
+ Tập xác định: \(\mathbb{R}\)
2. Đồ thị hàm số bậc hai
+) Đồ thị hàm số bậc hai \(y = f(x) = a{x^2} + bx + c\) \((a \ne 0)\) là một parabol (P):
- Đỉnh \(S\left( { - \frac{b}{{2a}}; - \frac{\Delta }{{4a}}} \right)\)
- Trục đối xứng: đường thẳng \(x = - \frac{b}{{2a}}\)
- Bề lõm: quay lên trên nếu \(a > 0\), quay xuống dưới nếu \(a < 0\)
- Cắt Oy tại điểm \((0;c)\)
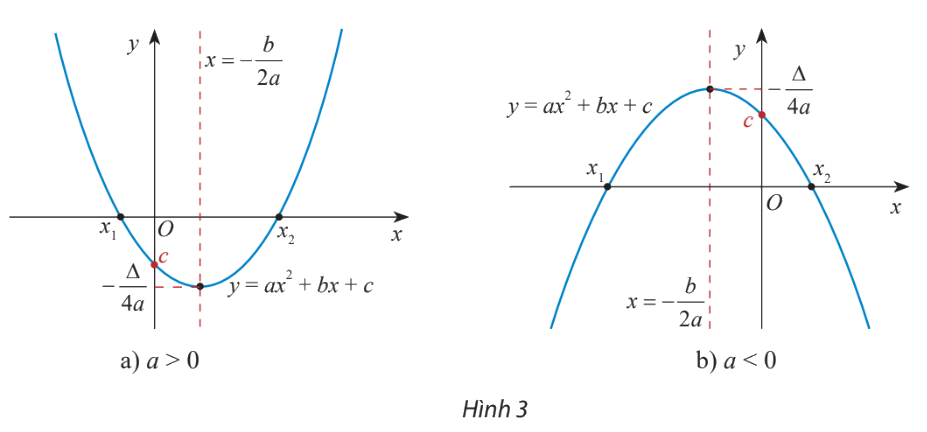
* Chú ý: Nếu PT \(a{x^2} + bx + c = 0\) có hai nghiệm \({x_1},{x_2}\) thì đồ thị hàm số \(y = a{x^2} + bx + c\) cắt trục hoành tại 2 điểm có hoành độ lần lượt là 2 nghiệm này.
+) Vẽ đồ thị
1) Xác định đỉnh \(S\left( { - \frac{b}{{2a}}; - \frac{\Delta }{{4a}}} \right)\)
2) Vẽ trục đối xứng d: \(x = - \frac{b}{{2a}}\)
3) Tìm tọa độ giao điểm của đồ thị với trục tung (A(0;c)), trục hoành (nếu có).
Xác định \(B\left( {\frac{{ - b}}{a};c} \right)\) (là điểm đối xứng với A qua d)
4) Vẽ parabol đỉnh S, trục đối xứng d, đi qua các điểm tìm được.
3. Sự biến thiên của hàm số bậc hai
+) Bảng biến thiên
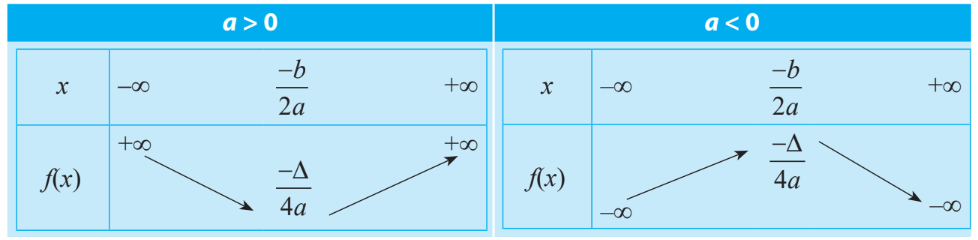
+) Kết luận:
\(a > 0\) | \(a < 0\) | |
Trên khoảng \(\left( { - \infty ;\frac{{ - b}}{{2a}}} \right)\) | Hàm số nghịch biến | Hàm số đồng biến |
Trên khoảng \(\left( {\frac{{ - b}}{{2a}}; + \infty } \right)\) | Hàm số đồng biến | Hàm số nghịch biến |
GTLN hoặc GTNN | Đạt GTNN bằng \(\frac{{ - \Delta }}{{4a}}\) tại \(x = \frac{{ - b}}{{2a}}\) | Đạt GTLN bằng \(\frac{{ - \Delta }}{{4a}}\) tại \(x = \frac{{ - b}}{{2a}}\) |
Tập giá trị | \(T = \left[ {\left. {\frac{{ - \Delta }}{{4a}}; + \infty } \right)} \right.\) | \(T = \left( {\left. { - \infty ;\frac{{ - \Delta }}{{4a}}} \right]} \right.\) |
4. Ứng dụng của hàm số bậc hai
+) Tầm bay cao và tầm bay xa
Chọn điểm \((0;{y_0})\) là điểm xuất phát thì phương trình quỹ đạo của cầu lông khi rời mặt vợt là:
\(y = \frac{{ - g.{x^2}}}{{2.{v_0}^2.{{\cos }^2}\alpha }} + \tan \alpha .x + {y_0}\)
Trong đó:
\(g\) là giá tốc trọng trường ( \( \approx 9,8\;m/{s^2}\))
\(\alpha \) là góc phát cầu (so với phương ngang của mặt đất)
\({v_0}\) là vận tốc ban đầu của cầu
\({y_0}\) là khoảng cách từ vị trí phát cầu đến mặt đất
Quỹ đạo chuyển động của cầu lông là một parabol.
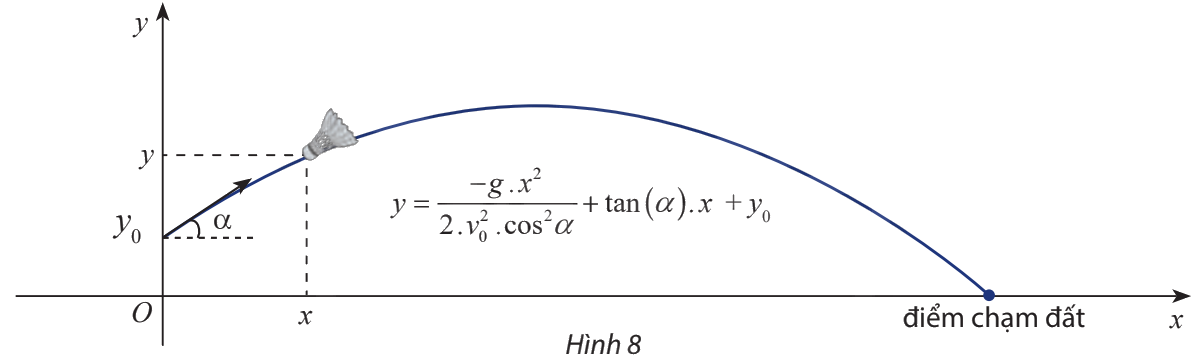
- Vị trí cao nhất tại đỉnh parabol, gọi là tầm bay cao;
- Khoảng cách từ nơi đứng phát cầu đến điểm cham đất, gọi là tầm bay xa.
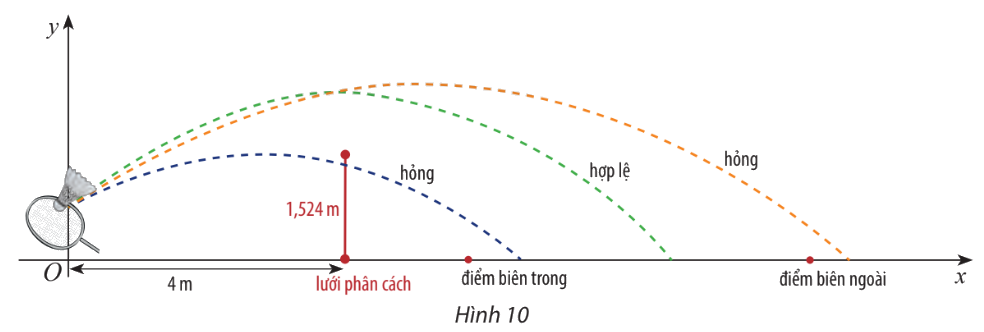
+) Bài toán ứng dụng
Khi cầu bay tới vị trí lưới phân cách, nếu nó ở bên trên mặt lưới và điểm rơi không ra khỏi đường biến phía sân đối phương thì lần phát cầu được xem là hợp lệ.
Hàm số bậc hai là một hàm số có dạng y = ax² + bx + c, trong đó a, b, c là các số thực và a ≠ 0. Đây là một trong những hàm số cơ bản và quan trọng nhất trong chương trình Toán học, đặc biệt là ở cấp trung học phổ thông.
Hàm số bậc hai được định nghĩa là hàm số có dạng y = ax² + bx + c, với a, b, c là các hệ số và a khác 0. Hệ số 'a' quyết định tính chất của parabol (độ mở và hướng). Hệ số 'b' và 'c' ảnh hưởng đến vị trí đỉnh và giao điểm của parabol với các trục tọa độ.
Tập xác định của hàm số bậc hai là tập hợp tất cả các số thực (ℝ). Điều này có nghĩa là hàm số có thể nhận bất kỳ giá trị nào của x. Tuy nhiên, tập giá trị của hàm số bậc hai phụ thuộc vào hệ số 'a'.
Đồ thị của hàm số bậc hai là một đường cong hình parabol. Parabol có những đặc điểm quan trọng sau:
Hệ số 'a' quyết định độ mở của parabol:
Hệ số 'a' cũng quyết định hướng của parabol:
Hệ số 'b' và 'c' ảnh hưởng đến vị trí đỉnh và giao điểm của parabol với các trục tọa độ. Việc xác định các yếu tố này giúp vẽ đồ thị hàm số một cách chính xác.
Phương trình bậc hai có dạng ax² + bx + c = 0. Nghiệm của phương trình bậc hai là các giá trị của x làm cho phương trình trở thành đúng. Mối liên hệ giữa phương trình bậc hai và hàm số bậc hai là:
Để hiểu rõ hơn về lý thuyết hàm số bậc hai, bạn có thể thực hành giải các bài tập sau:
Lý thuyết hàm số bậc hai là một phần quan trọng của chương trình Toán 10. Việc nắm vững các khái niệm, định lý và phương pháp giải bài tập liên quan đến hàm số bậc hai sẽ giúp bạn đạt kết quả tốt trong môn Toán và chuẩn bị cho các kiến thức nâng cao ở các lớp học tiếp theo. Hãy luyện tập thường xuyên và tìm kiếm sự hỗ trợ khi cần thiết để hiểu sâu hơn về chủ đề này.