Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 38, 39, 40 sách giáo khoa Toán 10 tập 2 chương trình Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong học tập.
Trong mặt phẳng Oxy, cho điểm M. Xác định tọa độ của vectơ OM Một máy bay đang cất cánh với vận tốc 240 km/h theo phương hợp với phương nằm ngang một góc 30 (hình 7) a) Tính độ dài mỗi cạnh của hình chữ nhật ABCD
Trong mặt phẳng Oxy, cho điểm M. Xác định tọa độ của vectơ \(\overrightarrow {OM} \)
Phương pháp giải:
Bước 1: Từ điểm M(x;y) xác định \({M_1},{M_2}\) lần lượt là hình chiếu vuông góc của M xuống trục hoành và trục tung
Bước 2: Tìm m, n sao cho \( \overrightarrow {OM_1}= m.\overrightarrow {i}; \, \overrightarrow {OM_2}=n.\overrightarrow {j} \)
Bước 3: Dựa vào quy tắc hình bình hành, suy ra tọa độ của vectơ \(\overrightarrow {OM}\) theo \( \overrightarrow {i}; \overrightarrow {j}\).
Lời giải chi tiết:
Cho điểm M(x;y) bất kì, xác định \({M_1},{M_2}\) lần lượt là hình chiếu vuông góc của M xuống trục hoành và trục tung
Dễ thấy \(\overrightarrow {O{M_1}}= x\overrightarrow i ; \, \overrightarrow {O{M_2}} = y \overrightarrow j \)
Áp dụng quy tắc hình bình hành ta có \(\overrightarrow {OM} = \overrightarrow {O{M_1}} + \overrightarrow {O{M_2}} = x\overrightarrow i + y\overrightarrow j \)
Vậy tọa độ của vectơ \(\overrightarrow {OM} \) là (x;y), trùng với tọa độ điểm M.
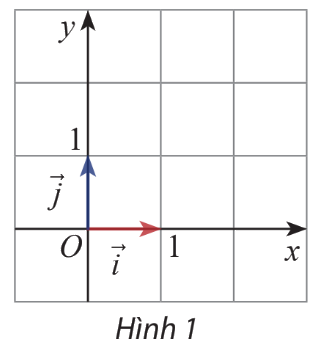
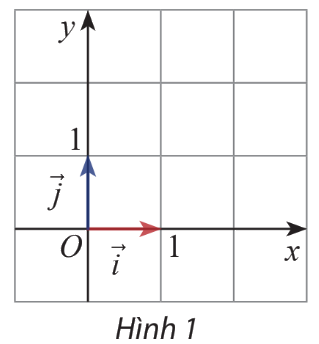
Nêu nhận xét về độ lớn, phương và chiều của vectơ trên trục \(Ox\) và vectơ \(\overrightarrow j \) trên trục \(Oy\) (hình 1)
Lời giải chi tiết:
+) Vectơ có độ lớn bằng 1 đơn vị, phương song song với trục \(Ox\)và cùng chiều với \(Ox\)
+) Vectơ \(\overrightarrow j \) có độ lớn bằng 1 đơn vị, phương song song với trục \(Oy\)và cùng chiều với \(Oy\)
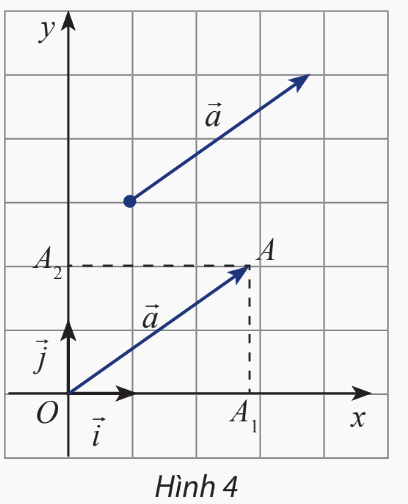
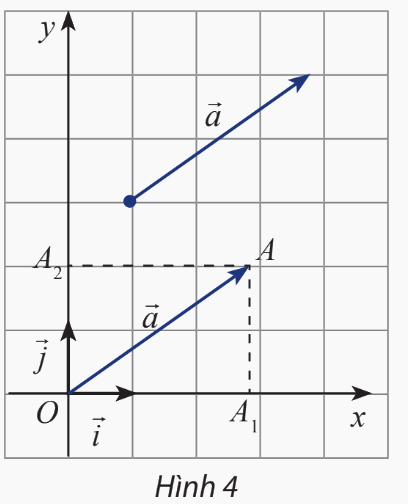
Trong mặt phẳng Oxy, cho một vectơ \(\overrightarrow a \)tùy ý. Vẽ \(\overrightarrow {OA} = \overrightarrow a \)và gọi \({A_1},{A_2}\)lần lượt là hình chiếu vuông góc của A lên Ox và Oy (hình 4). Đặt \({\overrightarrow {OA} _1} = x\overrightarrow i \), \({\overrightarrow {OA} _2} = y\overrightarrow j \). Biểu diễn vectơ \(\overrightarrow a \)theo hai vectơ và \(\overrightarrow j \)
Phương pháp giải:
Bước 1: Áp dụng quy tắc hình bình hành \(\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} \)
Bước 2: Dựa vào hình vẽ tìm x,y
Bước 3: Biểu diễn vectơ \(\overrightarrow a \)
Lời giải chi tiết:
Áp dụng quy tắc hình bình hành ta có \(\overrightarrow {OA} = \overrightarrow {O{A_1}} + \overrightarrow {O{A_2}} \)
Dựa vào hình vẽ ta thấy \({\overrightarrow {OA} _1} = 3\overrightarrow i \) và \({\overrightarrow {OA} _2} = 2\overrightarrow j \)
Vậy \(\overrightarrow a = \overrightarrow {OA} = \overrightarrow {O{A_1}} + \overrightarrow {O{A_2}} = 3\overrightarrow i + 2\overrightarrow j \)
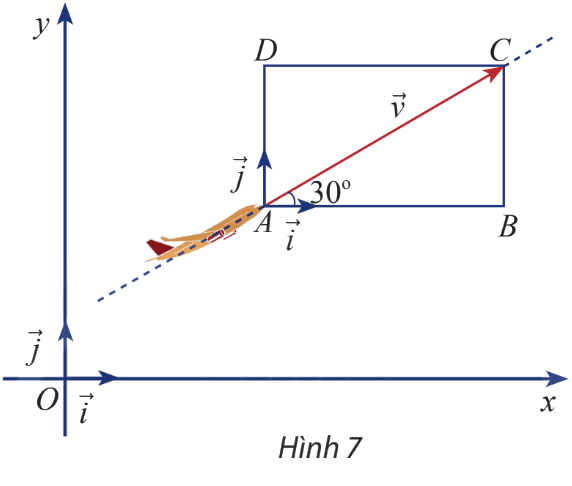
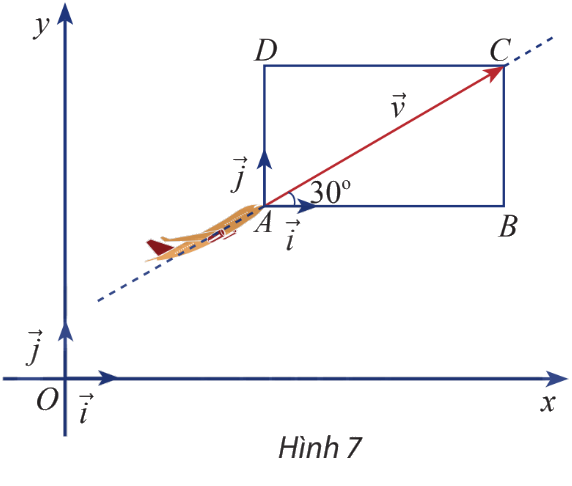
Một máy bay đang cất cánh với vận tốc 240 km/h theo phương hợp với phương nằm ngang một góc \(30^\circ \) (hình 7)
a) Tính độ dài mỗi cạnh của hình chữ nhật ABCD
b) Biểu diễn vận tốc \(\overrightarrow v \) theo hai vectơ và \(\overrightarrow j \)
c) Tìm tọa độ của \(\overrightarrow v \)
Lời giải chi tiết:
a) Vận tốc 240 km/h nên \(\left| {\overrightarrow v } \right| = AC = 240\)
Áp dụng các tính chất trong tam giác vuông ta có
\(AB = DC = AC.\cos (\widehat {CAB}) = 240.\cos (30^\circ ) = 120{\sqrt 3 }\)
\(AD = BC = AC.\sin (\widehat {CAB}) = 240.\sin (30^\circ ) = 120\)
b) Xem A là gốc tọa độ nên ta có \(\overrightarrow {AB} = 120\overrightarrow i ,\overrightarrow {AD} = 120{\sqrt 3 }\overrightarrow j ,\overrightarrow v = \overrightarrow {AC} = 120\overrightarrow i + 120{\sqrt 3 }\overrightarrow j \)
c)
Ta có \(\overrightarrow v = 120\overrightarrow i + 120{\sqrt 3 }\overrightarrow j \)
Vậy tọa độ của vectơ \(\overrightarrow v \) là \(\left( {120;120{\sqrt 3 }} \right)\)

Lời giải chi tiết:
Bàn cờ được chia thành 8 hàng (1-8) và 8 cột (a-h) đánh số như hình vẽ.
Do đó mỗi quân cờ xác định khi biết số hàng và số cột, tương ứng với cặp số (x;y) trong đó x là số hàng, y là số cột.
Khi đó hai mã đen có vị trí là (8;b) và (4;e)
Hai mã trắng có vị trí là (3;c) và (3;f)
Cách 2:
Đặt gốc tọa độ tại góc dưới, bên trái của bàn cờ. Coi mỗi ô vuông là 1 đơn vị.
Ta xác định được tọa độ của các con mã như sau:
Hai mã đen có tọa độ lần lượt là (2;8), (5;4)
Hai mã trắng có tọa độ lần lượt là (3;3) và (6;3)
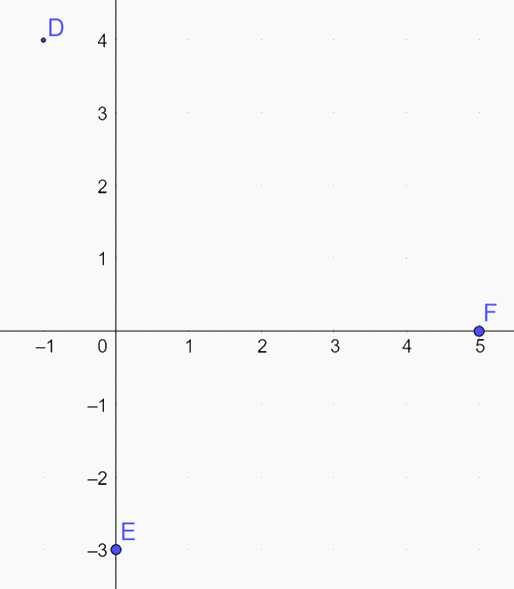
Trong mặt phẳng Oxy, cho ba điểm \(D\left( { - 1;4} \right),E\left( {0; - 3} \right),F\left( {5;0} \right)\)
a) Vẽ các điểm D, E, F trên mặt phẳng Oxy
b) Tìm tọa độ của các vectơ \(\overrightarrow {OD} ,\overrightarrow {OE} ,\overrightarrow {OF} \).
c) Vẽ và tìm tọa độ hai vectơ đơn vị và \(\overrightarrow j \)lần lượt trên hai trục tọa độ Ox và Oy
Lời giải chi tiết:
a)
b) Vì tọa độ vectơ \(\overrightarrow {OM} \) chính là tọa độ của điểm M (với mọi M) nên ta có:
\(\overrightarrow {OD} = \left( { - 1;4} \right),\overrightarrow {OE} = \left( {0; - 3} \right),\overrightarrow {OF} = \left( {5;0} \right)\)
c)
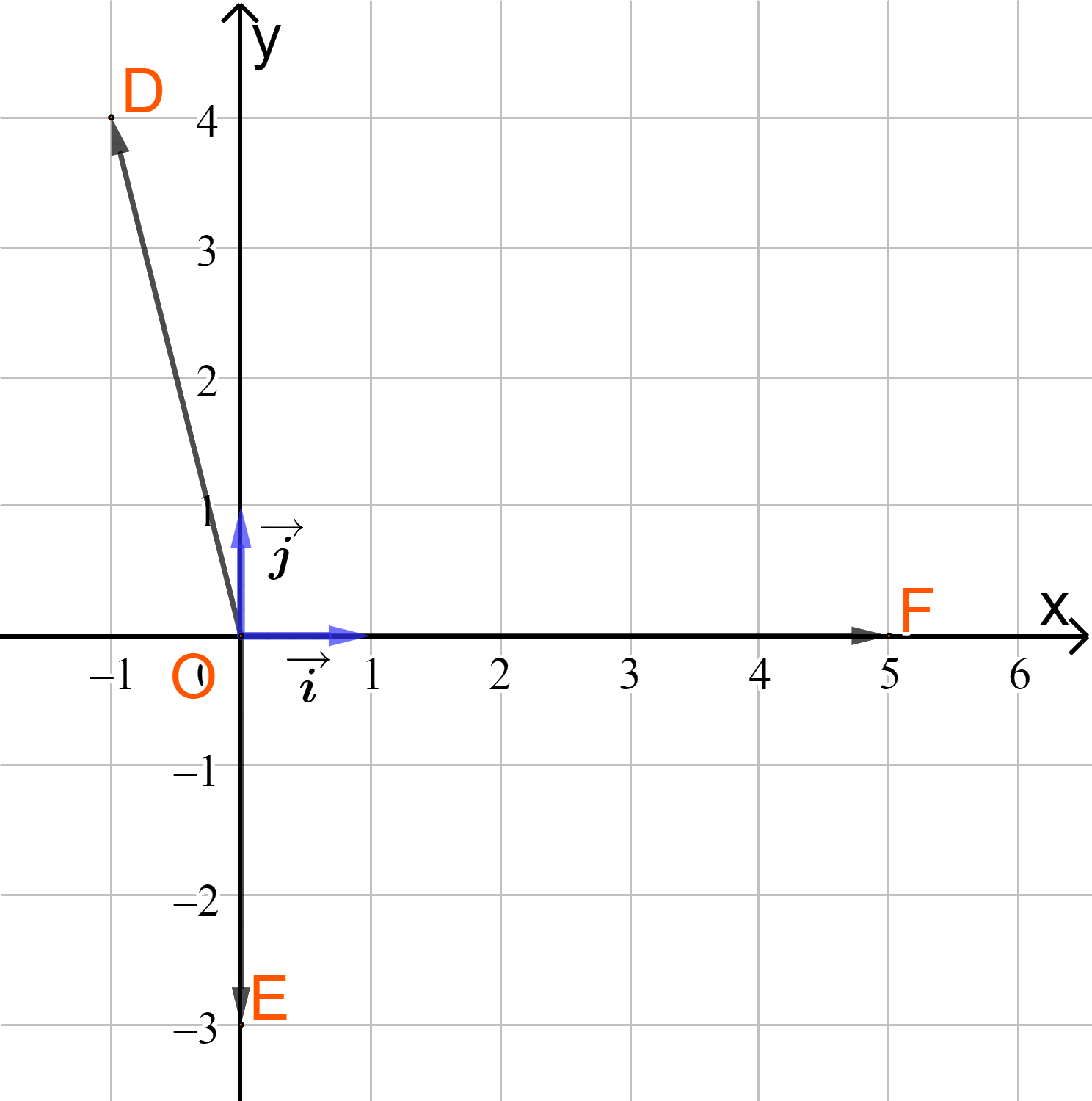
Từ hình vẽ ta có tọa độ của hai vectơ và \(\overrightarrow j \)là
và \(\overrightarrow j = (0;1)\)

Lời giải chi tiết:
Bàn cờ được chia thành 8 hàng (1-8) và 8 cột (a-h) đánh số như hình vẽ.
Do đó mỗi quân cờ xác định khi biết số hàng và số cột, tương ứng với cặp số (x;y) trong đó x là số hàng, y là số cột.
Khi đó hai mã đen có vị trí là (8;b) và (4;e)
Hai mã trắng có vị trí là (3;c) và (3;f)
Cách 2:
Đặt gốc tọa độ tại góc dưới, bên trái của bàn cờ. Coi mỗi ô vuông là 1 đơn vị.
Ta xác định được tọa độ của các con mã như sau:
Hai mã đen có tọa độ lần lượt là (2;8), (5;4)
Hai mã trắng có tọa độ lần lượt là (3;3) và (6;3)
Nêu nhận xét về độ lớn, phương và chiều của vectơ trên trục \(Ox\) và vectơ \(\overrightarrow j \) trên trục \(Oy\) (hình 1)
Lời giải chi tiết:
+) Vectơ có độ lớn bằng 1 đơn vị, phương song song với trục \(Ox\)và cùng chiều với \(Ox\)
+) Vectơ \(\overrightarrow j \) có độ lớn bằng 1 đơn vị, phương song song với trục \(Oy\)và cùng chiều với \(Oy\)
Trong mặt phẳng Oxy, cho một vectơ \(\overrightarrow a \)tùy ý. Vẽ \(\overrightarrow {OA} = \overrightarrow a \)và gọi \({A_1},{A_2}\)lần lượt là hình chiếu vuông góc của A lên Ox và Oy (hình 4). Đặt \({\overrightarrow {OA} _1} = x\overrightarrow i \), \({\overrightarrow {OA} _2} = y\overrightarrow j \). Biểu diễn vectơ \(\overrightarrow a \)theo hai vectơ và \(\overrightarrow j \)
Phương pháp giải:
Bước 1: Áp dụng quy tắc hình bình hành \(\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} \)
Bước 2: Dựa vào hình vẽ tìm x,y
Bước 3: Biểu diễn vectơ \(\overrightarrow a \)
Lời giải chi tiết:
Áp dụng quy tắc hình bình hành ta có \(\overrightarrow {OA} = \overrightarrow {O{A_1}} + \overrightarrow {O{A_2}} \)
Dựa vào hình vẽ ta thấy \({\overrightarrow {OA} _1} = 3\overrightarrow i \) và \({\overrightarrow {OA} _2} = 2\overrightarrow j \)
Vậy \(\overrightarrow a = \overrightarrow {OA} = \overrightarrow {O{A_1}} + \overrightarrow {O{A_2}} = 3\overrightarrow i + 2\overrightarrow j \)
Trong mặt phẳng Oxy, cho điểm M. Xác định tọa độ của vectơ \(\overrightarrow {OM} \)
Phương pháp giải:
Bước 1: Từ điểm M(x;y) xác định \({M_1},{M_2}\) lần lượt là hình chiếu vuông góc của M xuống trục hoành và trục tung
Bước 2: Tìm m, n sao cho \( \overrightarrow {OM_1}= m.\overrightarrow {i}; \, \overrightarrow {OM_2}=n.\overrightarrow {j} \)
Bước 3: Dựa vào quy tắc hình bình hành, suy ra tọa độ của vectơ \(\overrightarrow {OM}\) theo \( \overrightarrow {i}; \overrightarrow {j}\).
Lời giải chi tiết:
Cho điểm M(x;y) bất kì, xác định \({M_1},{M_2}\) lần lượt là hình chiếu vuông góc của M xuống trục hoành và trục tung
Dễ thấy \(\overrightarrow {O{M_1}}= x\overrightarrow i ; \, \overrightarrow {O{M_2}} = y \overrightarrow j \)
Áp dụng quy tắc hình bình hành ta có \(\overrightarrow {OM} = \overrightarrow {O{M_1}} + \overrightarrow {O{M_2}} = x\overrightarrow i + y\overrightarrow j \)
Vậy tọa độ của vectơ \(\overrightarrow {OM} \) là (x;y), trùng với tọa độ điểm M.
Trong mặt phẳng Oxy, cho ba điểm \(D\left( { - 1;4} \right),E\left( {0; - 3} \right),F\left( {5;0} \right)\)
a) Vẽ các điểm D, E, F trên mặt phẳng Oxy
b) Tìm tọa độ của các vectơ \(\overrightarrow {OD} ,\overrightarrow {OE} ,\overrightarrow {OF} \).
c) Vẽ và tìm tọa độ hai vectơ đơn vị và \(\overrightarrow j \)lần lượt trên hai trục tọa độ Ox và Oy
Lời giải chi tiết:
a)
b) Vì tọa độ vectơ \(\overrightarrow {OM} \) chính là tọa độ của điểm M (với mọi M) nên ta có:
\(\overrightarrow {OD} = \left( { - 1;4} \right),\overrightarrow {OE} = \left( {0; - 3} \right),\overrightarrow {OF} = \left( {5;0} \right)\)
c)
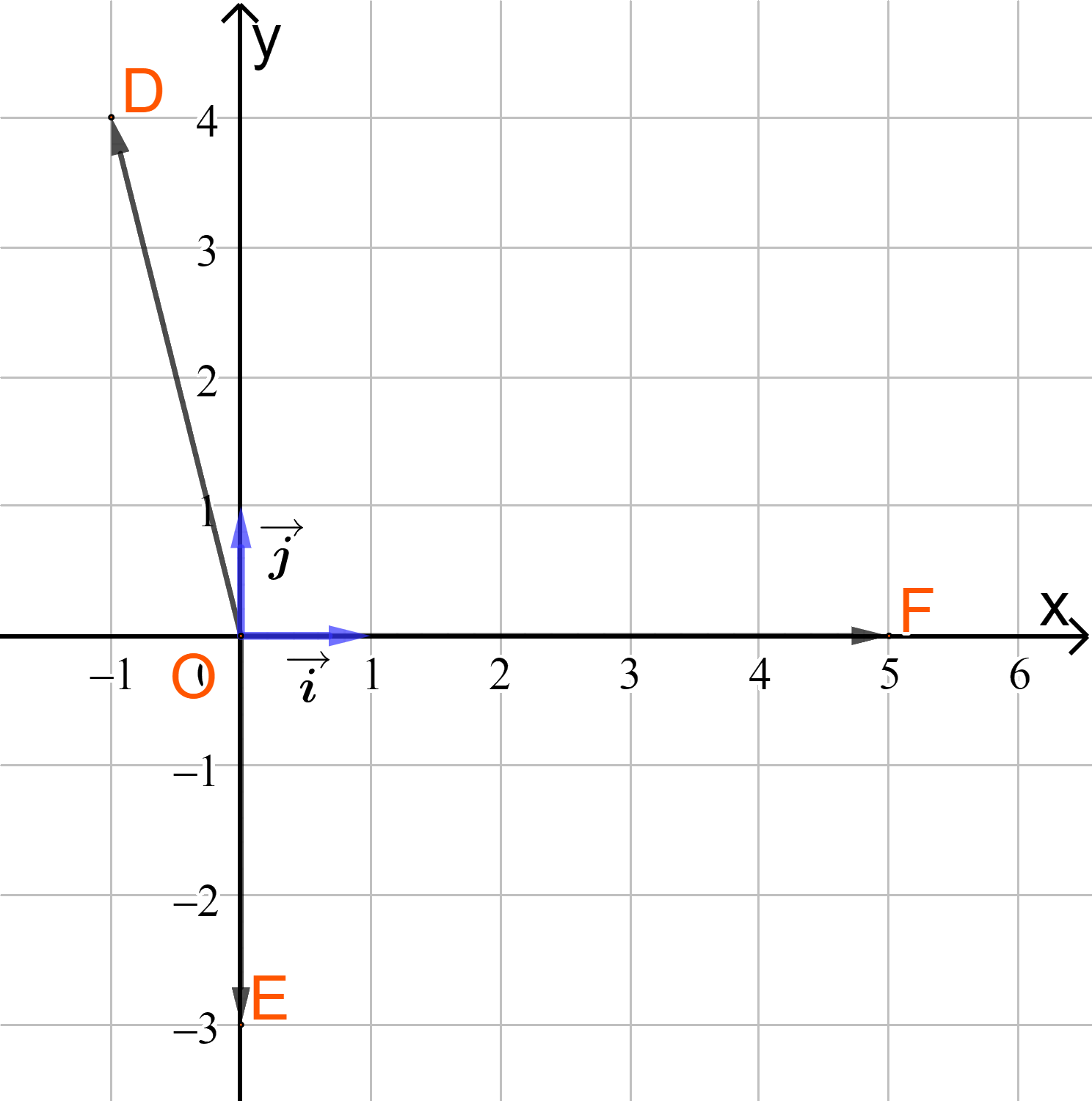
Từ hình vẽ ta có tọa độ của hai vectơ và \(\overrightarrow j \)là
và \(\overrightarrow j = (0;1)\)
Một máy bay đang cất cánh với vận tốc 240 km/h theo phương hợp với phương nằm ngang một góc \(30^\circ \) (hình 7)
a) Tính độ dài mỗi cạnh của hình chữ nhật ABCD
b) Biểu diễn vận tốc \(\overrightarrow v \) theo hai vectơ và \(\overrightarrow j \)
c) Tìm tọa độ của \(\overrightarrow v \)
Lời giải chi tiết:
a) Vận tốc 240 km/h nên \(\left| {\overrightarrow v } \right| = AC = 240\)
Áp dụng các tính chất trong tam giác vuông ta có
\(AB = DC = AC.\cos (\widehat {CAB}) = 240.\cos (30^\circ ) = 120{\sqrt 3 }\)
\(AD = BC = AC.\sin (\widehat {CAB}) = 240.\sin (30^\circ ) = 120\)
b) Xem A là gốc tọa độ nên ta có \(\overrightarrow {AB} = 120\overrightarrow i ,\overrightarrow {AD} = 120{\sqrt 3 }\overrightarrow j ,\overrightarrow v = \overrightarrow {AC} = 120\overrightarrow i + 120{\sqrt 3 }\overrightarrow j \)
c)
Ta có \(\overrightarrow v = 120\overrightarrow i + 120{\sqrt 3 }\overrightarrow j \)
Vậy tọa độ của vectơ \(\overrightarrow v \) là \(\left( {120;120{\sqrt 3 }} \right)\)
Mục 1 của chương trình Toán 10 tập 2 Chân trời sáng tạo tập trung vào việc ôn tập và mở rộng kiến thức về vectơ. Các bài tập trang 38, 39, 40 xoay quanh các chủ đề chính như:
Bài 1: (Trang 38) Cho hai vectơ a và b. Tìm vectơ c sao cho a + b = c.
Lời giải: Để tìm vectơ c, ta thực hiện phép cộng vectơ theo quy tắc hình bình hành hoặc quy tắc tam giác. Cụ thể, ta vẽ hình bình hành ABCD với AB = a và AD = b. Khi đó, vectơ AC chính là vectơ c cần tìm.
Bài 2: (Trang 39) Tính tích vô hướng của hai vectơ a = (1; 2) và b = (-3; 4).
Lời giải: Tích vô hướng của hai vectơ a = (x1; y1) và b = (x2; y2) được tính theo công thức: a.b = x1x2 + y1y2. Áp dụng công thức này, ta có:
a.b = (1)(-3) + (2)(4) = -3 + 8 = 5.
Bài 3: (Trang 40) Cho tam giác ABC với A(0; 0), B(1; 2), C(-1; 1). Tính góc BAC.
Lời giải: Để tính góc BAC, ta sử dụng công thức tính cosin góc giữa hai vectơ:
cos(BAC) = (AB.AC) / (||AB|| . ||AC||)
Trước hết, ta tính các vectơ:
Sau đó, ta tính tích vô hướng và độ dài của các vectơ:
Cuối cùng, ta tính cosin góc BAC:
cos(BAC) = 1 / (√5 . √2) = 1 / √10 ≈ 0.316
Vậy, BAC ≈ 71.57°.
Để giải tốt các bài tập về vectơ, các em cần nắm vững các kiến thức cơ bản như:
Ngoài ra, các em nên luyện tập thường xuyên để rèn luyện kỹ năng giải toán và làm quen với các dạng bài tập khác nhau.
Hy vọng với lời giải chi tiết và hướng dẫn cụ thể trên đây, các em đã hiểu rõ cách giải các bài tập mục 1 trang 38, 39, 40 SGK Toán 10 tập 2 Chân trời sáng tạo. Chúc các em học tập tốt!