Bài 3 trang 85 SGK Toán 10 tập 2 thuộc chương trình Toán 10 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về vectơ và ứng dụng của vectơ trong hình học. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho bài 3 trang 85 SGK Toán 10 tập 2, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Hộp thứ nhất đựng 1 thẻ xanh, 1 thẻ đỏ và 1 thẻ vàng. Hộp thứ hai đựng 1 thẻ xanh, 1 thẻ đỏ. Các tấm thẻ có kích thước có khối lượng như nhau. Lần lượt lấy ra ngẫu nhiên từ mỗi hộp một tấm thẻ
Đề bài
Hộp thứ nhất đựng 1 thẻ xanh, 1 thẻ đỏ và 1 thẻ vàng. Hộp thứ hai đựng 1 thẻ xanh và 1 thẻ đỏ. Các tấm thẻ có kích thước và khối lượng như nhau. Lần lượt lấy ra ngẫu nhiên từ mỗi hộp một tấm thẻ.
a) Sử dụng sơ đồ hình cây, hãy liệt kê tất cả các kết quả có thể xảy ra.
b) Tính xác suất của biến cố “Trong 2 thẻ lấy ra có ít nhất 1 thẻ màu đỏ”.
Lời giải chi tiết
a) Các kết quả có thể xảy ra trong 2 lần lấy tấm thẻ từ 2 hộp được thể hiện ở sơ đồ hình cây như hình dưới đây:
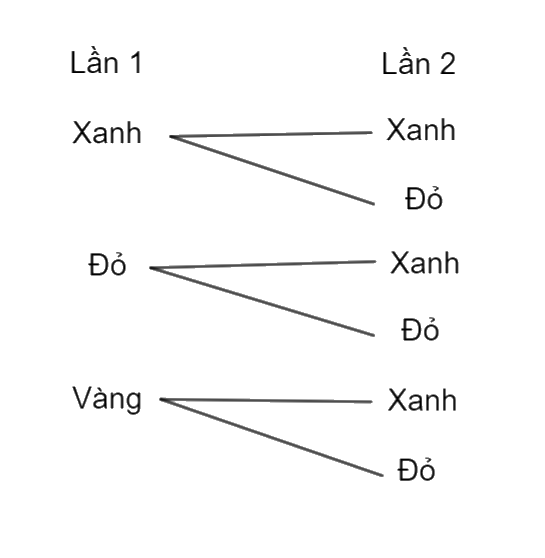
b)
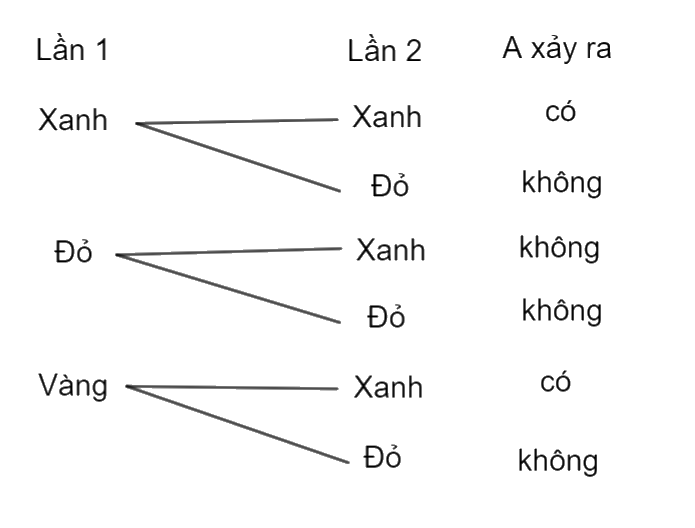
Gọi A là biến cố “Trong 2 thẻ lấy ra không có thẻ màu đỏ nào” là biến cố đối của biến cố “Trong 2 thẻ lấy ra có ít nhất 1 thẻ màu đỏ”.
Dựa vào sơ đồ hình cây ta thấy có tất cả 6 kết quả có thể xảy ra, trong đó có 2 kết quả thuận lợi cho A. Do đó: \(P(A) = \frac{2}{6} = \frac{1}{3}\).
Vậy xác suất của biến cố “Trong 2 thẻ lấy ra có ít nhất 1 thẻ màu đỏ” là \(1 - \frac{1}{3} = \frac{2}{3}\).
Bài 3 trang 85 SGK Toán 10 tập 2 Chân trời sáng tạo là một bài toán ứng dụng thực tế về vectơ. Để giải bài toán này, học sinh cần nắm vững các kiến thức về:
Bài 3 thường đưa ra một tình huống thực tế liên quan đến các vật thể chuyển động hoặc các lực tác động. Học sinh cần phân tích tình huống, xác định các vectơ liên quan và sử dụng các kiến thức đã học để giải quyết bài toán.
Để giúp học sinh hiểu rõ hơn về cách giải bài 3 trang 85 SGK Toán 10 tập 2, chúng ta sẽ cùng nhau phân tích một ví dụ cụ thể:
Ví dụ: Cho tam giác ABC có A(1;2), B(3;4), C(-1;0). Tính độ dài đường cao hạ từ A xuống cạnh BC.
BC = C - B = (-1 - 3; 0 - 4) = (-4; -4)
Đường thẳng BC có dạng: ax + by + c = 0. Ta có vectơ pháp tuyến của BC là n = (1; 1). Vậy phương trình đường thẳng BC là: 1(x - 3) + 1(y - 4) = 0 ⇔ x + y - 7 = 0
Khoảng cách từ A(1;2) đến đường thẳng x + y - 7 = 0 là: d(A, BC) = |1 + 2 - 7| / √(1² + 1²) = |-4| / √2 = 4/√2 = 2√2
Vậy độ dài đường cao hạ từ A xuống cạnh BC là 2√2.
Ngoài bài 3 trang 85, SGK Toán 10 tập 2 Chân trời sáng tạo còn có nhiều bài tập tương tự khác. Các bài tập này thường yêu cầu học sinh:
Để học tốt môn Toán 10, học sinh có thể tham khảo thêm các tài liệu sau:
Bài 3 trang 85 SGK Toán 10 tập 2 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về vectơ và ứng dụng của vectơ trong hình học. Hy vọng với hướng dẫn chi tiết và các mẹo giải bài tập trên, các em học sinh sẽ tự tin giải quyết bài toán này và các bài tập tương tự.