Chào mừng các em học sinh đến với lời giải chi tiết bài 1 trang 32 SGK Toán 10 tập 1 – Chân trời sáng tạo. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập một cách dễ hiểu và hiệu quả.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, giúp các em nắm vững kiến thức và đạt kết quả tốt nhất.
Cho bất phương trình bậc nhất hai ẩn x - 2y + 6 > 0 a) (0;0) có phải là một nghiệm của bất phương trình đã cho không? b) Chỉ ra ba cặp số (x;y) là nghiệm của bất phương trình đã cho. c) Biểu diễn miền nghiệm của các bất phương trình đã cho trên mặt phẳng tọa độ Oxy
Đề bài
Cho bất phương trình bậc nhất hai ẩn \(x - 2y + 6 > 0\)
a) (0;0) có phải là một nghiệm của bất phương trình đã cho không?
b) Chỉ ra ba cặp số (x;y) là nghiệm của bất phương trình đã cho.
c) Biểu diễn miền nghiệm của các bất phương trình đã cho trên mặt phẳng tọa độ Oxy
Lời giải chi tiết
a) Vì \(0 - 2.0 + 6 = 6 > 0\) nên (0;0) là một nghiệm của bất phương trình đã cho.
b) Vì \(0 - 2.1 + 6 = 4 > 0\) nên (0;1) là một nghiệm của bất phương trình đã cho.
Vì \(1 - 2.0 + 6 = 7 > 0\) nên (1;0) là một nghiệm của bất phương trình đã cho.
Vì \(1 - 2.1 + 6 = 5 > 0\) nên (1;1) là một nghiệm của bất phương trình đã cho.
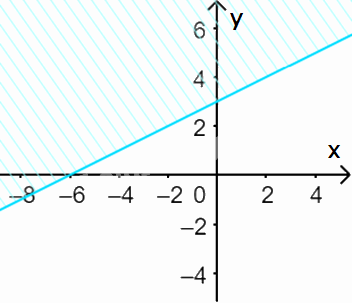
c) Vẽ đường thẳng \(\Delta :x - 2y + 6 = 0\) đi qua hai điểm \(A(0;3)\) và \(B\left( { - 2;2} \right)\)
Xét gốc tọa độ \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \(0 - 2.0 + 6 = 6 > 0\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng không kể bờ \(\Delta \), chứa gốc tọa độ O
(miền không gạch chéo trên hình)
Bài 1 trang 32 SGK Toán 10 tập 1 – Chân trời sáng tạo thuộc chương 1: Mệnh đề và tập hợp. Bài tập này yêu cầu học sinh vận dụng kiến thức về mệnh đề, tập hợp, các phép toán trên tập hợp để giải quyết các bài toán cụ thể. Việc nắm vững lý thuyết và kỹ năng giải bài tập là vô cùng quan trọng để xây dựng nền tảng vững chắc cho các kiến thức toán học ở các lớp trên.
Bài 1 trang 32 SGK Toán 10 tập 1 – Chân trời sáng tạo thường bao gồm các dạng bài tập sau:
Để giúp các em hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ đi vào phân tích từng phần của bài tập.
...
...
...
Để giải quyết hiệu quả các bài tập về mệnh đề và tập hợp, các em cần lưu ý những điều sau:
Ví dụ 1: Cho A = {1, 2, 3} và B = {2, 4, 5}. Tìm A ∪ B.
Lời giải: A ∪ B = {1, 2, 3, 4, 5}.
Ví dụ 2: Cho A = {1, 2, 3} và B = {2, 3, 4}. Tìm A ∩ B.
Lời giải: A ∩ B = {2, 3}.
Hy vọng với lời giải chi tiết và những lưu ý trên, các em sẽ tự tin hơn khi giải bài 1 trang 32 SGK Toán 10 tập 1 – Chân trời sáng tạo và các bài tập tương tự. Chúc các em học tập tốt!