Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 3 trang 68, 69, 70 sách giáo khoa Toán 10 tập 2 - Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong học tập.
Viết phương trình chính tắc của parabol (P) có đường chuẩn Một cổng chào có hình parabol cao 10 m và bề rộng của cổng tại chân cổng là 5 m. Tính bề rộng của cổng tại chỗ cách đỉnh 2 m
Viết phương trình chính tắc của parabol (P) có đường chuẩn \(\Delta :x + 1 = 0\).
Phương pháp giải:
Bước 1: Từ phương trình đường chuẩn tìm tọa độ của tiêu điểm (phương trình đường chuẩn có dạng \(x + \frac{p}{2} = 0\).
Bước 2: Viết phương trình chính tắc của parabol có dạng \({y^2} = 2px\) với \(M(x;y) \in (P)\).
Lời giải chi tiết:
Từ phương trình đường chuẩn \(\Delta :x + 1 = 0\) ta có tiêu điểm \(F\left( {1;0} \right)\).
Phương trình chính tắc của parabol có dạng \({y^2} = 2x\).
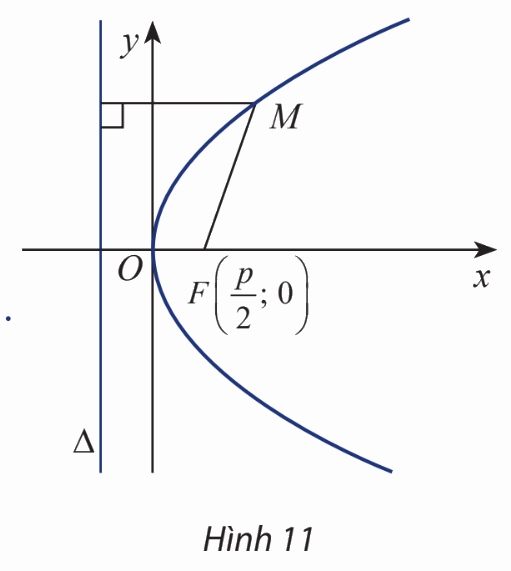
Cho parabol (P) có tiêu điểm F và đường chuẩn \(\Delta \). Gọi khoảng cách từ tiêu điểm đến đường chuẩn là p, hiển nhiên \(p > 0\).
Chọn hệ trục tọa độ Oxy sao cho \(F\left( {\frac{p}{2};0} \right)\) và \(\Delta :x + \frac{p}{2} = 0\).
Xét điểm \(M(x;y)\).
a) Tính MF và \(d\left( {M,\Delta } \right)\).
b) Giải thích biểu thức sau:
\(M(x;y) \in (P) \Leftrightarrow \sqrt {{{\left( {x - \frac{p}{2}} \right)}^2} + {y^2}} = \left| {x + \frac{p}{2}} \right|\).
Phương pháp giải:
Sử dụng phương pháp tọa độ trong mặt phẳng.
Lời giải chi tiết:
a) Ta có: \(\overrightarrow {FM} = \left( {x - \frac{p}{2};y} \right) \Rightarrow MF = \left| {\overrightarrow {FM} } \right| = \sqrt {{{\left( {x - \frac{p}{2}} \right)}^2} + {y^2}} \).
\(d\left( {M,\Delta } \right) = \frac{{\left| {x + \frac{p}{2}} \right|}}{1} = \left| {x + \frac{p}{2}} \right|\).
b) M thuộc parabol (P) nên M cách đều F và \(\Delta \).
Suy ra \(MF = d\left( {M,\Delta } \right) \Leftrightarrow \sqrt {{{\left( {x - \frac{p}{2}} \right)}^2} + {y^2}} = \left| {x - \frac{p}{2}} \right|\).
Một cổng chào có hình parabol cao 10 m và bề rộng của cổng tại chân cổng là 5 m. Tính bề rộng của cổng tại chỗ cách đỉnh 2 m.
Phương pháp giải:
Bước 1: Gọi phương trình của parabol một cách tổng quát.
Bước 2: Thay các giả thiết tìm tiêu điểm.
Bước 3: Thay \(x = 2\) vào phương trình chính tắc tìm y.
Lời giải chi tiết:
Vẽ lại parabol và chọn hệ trục tọa độ như hình dưới.
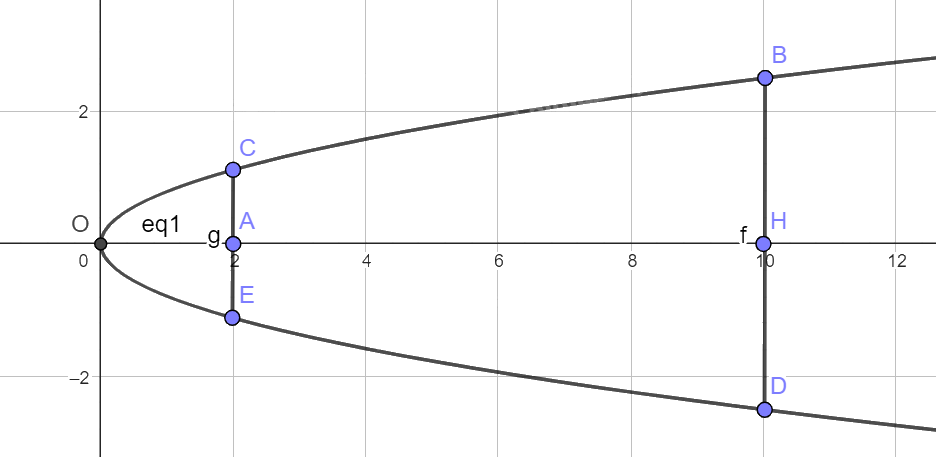
Gọi phương trình của parabol là \({y^2} = 2px\).
Ta có chiều cao của cổng \(OH = 10\), chiều rộng tại chân cổng \(BD = 2BH = 5\).
Vậy điểm B có tọa độ là \(B\left( {10;\frac{5}{2}} \right)\).
Thay tọa độ điểm B vào phương trình parabol ta có:
\({\left( {\frac{5}{2}} \right)^2} = 2p.10 \Rightarrow p = \frac{5}{{16}}\), suy ra phương trình parabol có dạng \({y^2} = \frac{5}{8}x\).
Thay \(x = 2\) vào phương trình \({y^2} = \frac{5}{8}x\) ta tìm được \(y = CA = \frac{{\sqrt 5 }}{2} \).
Vậy bề rộng của cổng tại chỗ cách đỉnh 2 m là \(\sqrt 5 \) m.
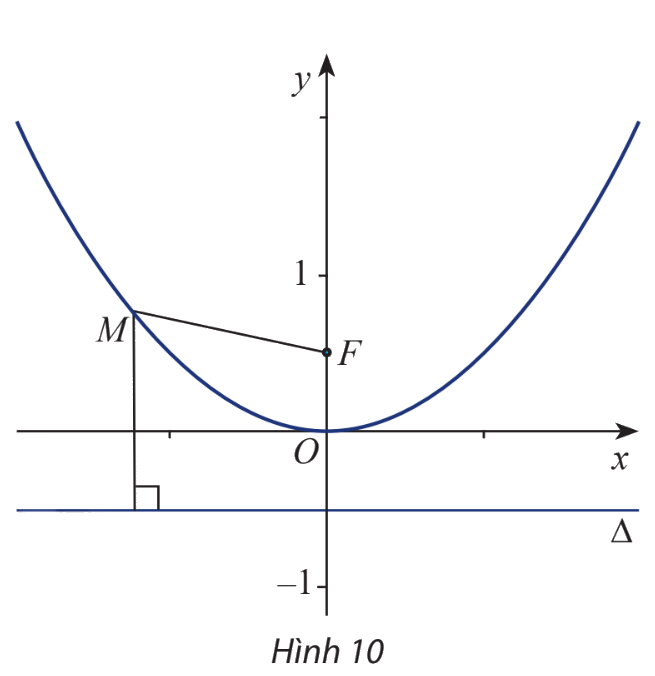
Trong mặt phẳng Oxy, cho điểm \(F\left( {0;\frac{1}{2}} \right)\), đường thẳng \(\Delta :y + \frac{1}{2} = 0\) và điểm \(M(x;y)\). Để tìm hệ thức giữa x và y sao cho \(M\) cách đều F và \(\Delta \), một học sinh đã làm như sau:
+) Tính MF và MH (với H là hình chiếu của M trên \(\Delta \)):
\(MF = \sqrt {{x^2} + {{\left( {y - \frac{1}{2}} \right)}^2}} ,MH = d\left( {M,\Delta } \right) = \left| {y + \frac{1}{2}} \right|\)
+) Điều kiện để M cách đều F và \(\Delta \):
\(\begin{array}{l}MF = d\left( {M,\Delta } \right) \Leftrightarrow \sqrt {{x^2} + {{\left( {y - \frac{1}{2}} \right)}^2}} = \left| {y + \frac{1}{2}} \right|\\ \Leftrightarrow {x^2} + {\left( {y - \frac{1}{2}} \right)^2} = {\left( {y + \frac{1}{2}} \right)^2}\\ \Leftrightarrow {x^2} = 2y \Leftrightarrow y = \frac{1}{2}{x^2}\left( * \right)\end{array}\)
Hãy cho biết tên đồ thị (P) của hàm số (*) vừa tìm được.
Lời giải chi tiết:
Đồ thị của hàm số (*) vừa tìm được có dạng là hàm số bậc 2 khuyết b và c tập hợp các điểm cách đều nhau qua một đường thẳng, đồ thị của hàm bậc 2 này có tên gọi là parabol.
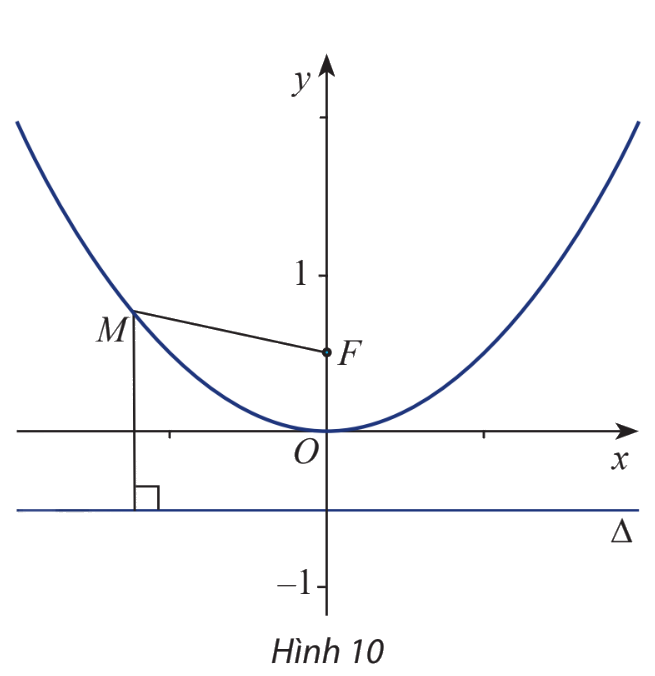
Trong mặt phẳng Oxy, cho điểm \(F\left( {0;\frac{1}{2}} \right)\), đường thẳng \(\Delta :y + \frac{1}{2} = 0\) và điểm \(M(x;y)\). Để tìm hệ thức giữa x và y sao cho \(M\) cách đều F và \(\Delta \), một học sinh đã làm như sau:
+) Tính MF và MH (với H là hình chiếu của M trên \(\Delta \)):
\(MF = \sqrt {{x^2} + {{\left( {y - \frac{1}{2}} \right)}^2}} ,MH = d\left( {M,\Delta } \right) = \left| {y + \frac{1}{2}} \right|\)
+) Điều kiện để M cách đều F và \(\Delta \):
\(\begin{array}{l}MF = d\left( {M,\Delta } \right) \Leftrightarrow \sqrt {{x^2} + {{\left( {y - \frac{1}{2}} \right)}^2}} = \left| {y + \frac{1}{2}} \right|\\ \Leftrightarrow {x^2} + {\left( {y - \frac{1}{2}} \right)^2} = {\left( {y + \frac{1}{2}} \right)^2}\\ \Leftrightarrow {x^2} = 2y \Leftrightarrow y = \frac{1}{2}{x^2}\left( * \right)\end{array}\)
Hãy cho biết tên đồ thị (P) của hàm số (*) vừa tìm được.
Lời giải chi tiết:
Đồ thị của hàm số (*) vừa tìm được có dạng là hàm số bậc 2 khuyết b và c tập hợp các điểm cách đều nhau qua một đường thẳng, đồ thị của hàm bậc 2 này có tên gọi là parabol.
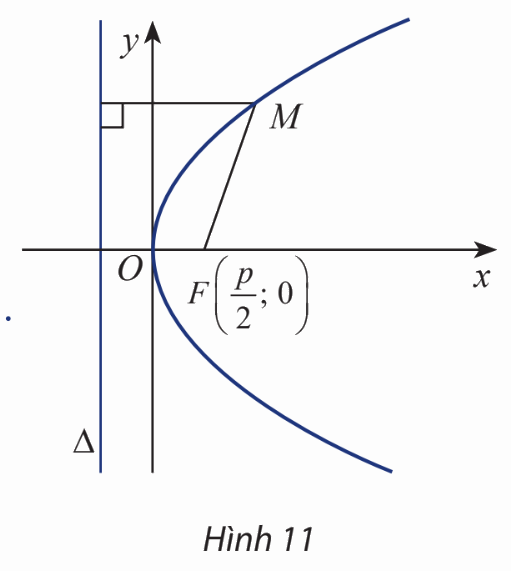
Cho parabol (P) có tiêu điểm F và đường chuẩn \(\Delta \). Gọi khoảng cách từ tiêu điểm đến đường chuẩn là p, hiển nhiên \(p > 0\).
Chọn hệ trục tọa độ Oxy sao cho \(F\left( {\frac{p}{2};0} \right)\) và \(\Delta :x + \frac{p}{2} = 0\).
Xét điểm \(M(x;y)\).
a) Tính MF và \(d\left( {M,\Delta } \right)\).
b) Giải thích biểu thức sau:
\(M(x;y) \in (P) \Leftrightarrow \sqrt {{{\left( {x - \frac{p}{2}} \right)}^2} + {y^2}} = \left| {x + \frac{p}{2}} \right|\).
Phương pháp giải:
Sử dụng phương pháp tọa độ trong mặt phẳng.
Lời giải chi tiết:
a) Ta có: \(\overrightarrow {FM} = \left( {x - \frac{p}{2};y} \right) \Rightarrow MF = \left| {\overrightarrow {FM} } \right| = \sqrt {{{\left( {x - \frac{p}{2}} \right)}^2} + {y^2}} \).
\(d\left( {M,\Delta } \right) = \frac{{\left| {x + \frac{p}{2}} \right|}}{1} = \left| {x + \frac{p}{2}} \right|\).
b) M thuộc parabol (P) nên M cách đều F và \(\Delta \).
Suy ra \(MF = d\left( {M,\Delta } \right) \Leftrightarrow \sqrt {{{\left( {x - \frac{p}{2}} \right)}^2} + {y^2}} = \left| {x - \frac{p}{2}} \right|\).
Viết phương trình chính tắc của parabol (P) có đường chuẩn \(\Delta :x + 1 = 0\).
Phương pháp giải:
Bước 1: Từ phương trình đường chuẩn tìm tọa độ của tiêu điểm (phương trình đường chuẩn có dạng \(x + \frac{p}{2} = 0\).
Bước 2: Viết phương trình chính tắc của parabol có dạng \({y^2} = 2px\) với \(M(x;y) \in (P)\).
Lời giải chi tiết:
Từ phương trình đường chuẩn \(\Delta :x + 1 = 0\) ta có tiêu điểm \(F\left( {1;0} \right)\).
Phương trình chính tắc của parabol có dạng \({y^2} = 2x\).
Một cổng chào có hình parabol cao 10 m và bề rộng của cổng tại chân cổng là 5 m. Tính bề rộng của cổng tại chỗ cách đỉnh 2 m.
Phương pháp giải:
Bước 1: Gọi phương trình của parabol một cách tổng quát.
Bước 2: Thay các giả thiết tìm tiêu điểm.
Bước 3: Thay \(x = 2\) vào phương trình chính tắc tìm y.
Lời giải chi tiết:
Vẽ lại parabol và chọn hệ trục tọa độ như hình dưới.
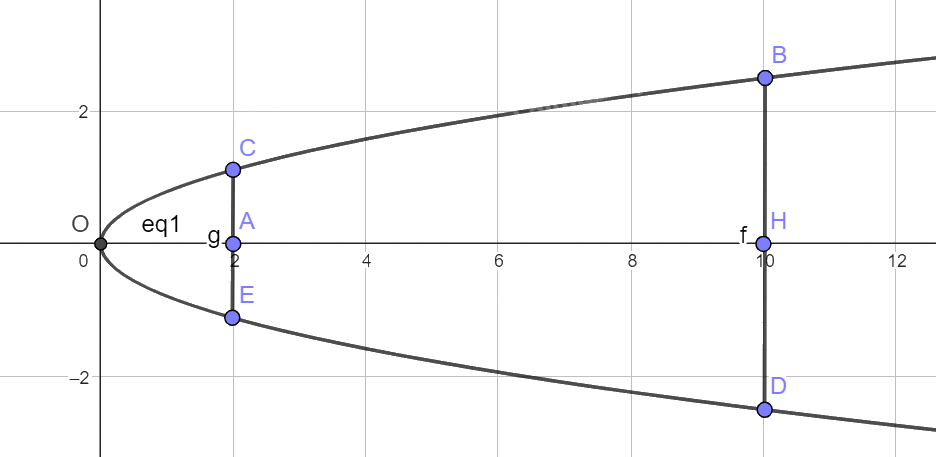
Gọi phương trình của parabol là \({y^2} = 2px\).
Ta có chiều cao của cổng \(OH = 10\), chiều rộng tại chân cổng \(BD = 2BH = 5\).
Vậy điểm B có tọa độ là \(B\left( {10;\frac{5}{2}} \right)\).
Thay tọa độ điểm B vào phương trình parabol ta có:
\({\left( {\frac{5}{2}} \right)^2} = 2p.10 \Rightarrow p = \frac{5}{{16}}\), suy ra phương trình parabol có dạng \({y^2} = \frac{5}{8}x\).
Thay \(x = 2\) vào phương trình \({y^2} = \frac{5}{8}x\) ta tìm được \(y = CA = \frac{{\sqrt 5 }}{2} \).
Vậy bề rộng của cổng tại chỗ cách đỉnh 2 m là \(\sqrt 5 \) m.
Mục 3 trong SGK Toán 10 tập 2 - Chân trời sáng tạo tập trung vào việc ứng dụng kiến thức về vectơ trong hình học. Cụ thể, các bài tập trong mục này thường liên quan đến việc xác định tọa độ của vectơ, thực hiện các phép toán vectơ (cộng, trừ, nhân với một số thực) và sử dụng vectơ để chứng minh các tính chất hình học.
Bài tập này yêu cầu học sinh xác định tọa độ của một vectơ dựa trên tọa độ của các điểm đầu và điểm cuối của vectơ đó. Để giải bài tập này, học sinh cần nắm vững công thức tính tọa độ của vectơ: Nếu A(xA, yA) và B(xB, yB) thì vectơ AB có tọa độ là (xB - xA, yB - yA).
Ví dụ: Cho A(1, 2) và B(3, 5). Tìm tọa độ của vectơ AB.
Giải: Vectơ AB có tọa độ là (3 - 1, 5 - 2) = (2, 3).
Bài tập này yêu cầu học sinh thực hiện các phép toán cộng, trừ, nhân với một số thực trên các vectơ. Để giải bài tập này, học sinh cần nắm vững các quy tắc sau:
Ví dụ: Cho vectơ a = (1, 2) và vectơ b = (3, 4). Tính vectơ a + b và 2a.
Giải: Vectơ a + b = (1 + 3, 2 + 4) = (4, 6). Vectơ 2a = (2*1, 2*2) = (2, 4).
Bài tập này yêu cầu học sinh sử dụng kiến thức về vectơ để chứng minh các tính chất hình học như chứng minh hai đường thẳng song song, chứng minh hai tam giác bằng nhau, chứng minh một điểm nằm trên một đường thẳng,...
Ví dụ: Cho tam giác ABC. Gọi M là trung điểm của BC. Chứng minh rằng vectơ AM = (vectơ AB + vectơ AC) / 2.
Giải: Vì M là trung điểm của BC nên BM = MC. Do đó, vectơ BM = vectơ MC. Ta có: vectơ AM = vectơ AB + vectơ BM = vectơ AB + vectơ MC = vectơ AB + (vectơ AC - vectơ AM). Suy ra: 2 vectơ AM = vectơ AB + vectơ AC. Vậy vectơ AM = (vectơ AB + vectơ AC) / 2.
Khi giải các bài tập về vectơ, học sinh cần chú ý các điểm sau:
Ngoài SGK Toán 10 tập 2 - Chân trời sáng tạo, học sinh có thể tham khảo thêm các tài liệu sau để nắm vững kiến thức về vectơ:
Hy vọng với lời giải chi tiết và những lưu ý trên, các em học sinh sẽ tự tin hơn khi giải các bài tập trong mục 3 trang 68, 69, 70 SGK Toán 10 tập 2 - Chân trời sáng tạo. Chúc các em học tập tốt!