Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 3 trang 100, 101 SGK Toán 10 tập 1 chương trình Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập một cách khoa học.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, tự tin giải quyết các bài toán Toán 10 và đạt kết quả tốt nhất trong học tập.
Cho hai vectơ i, j vuông góc có cùng độ dài bằng 1. Phân tử sulfur dioxide SO2 có cấu tạo hình chữ V, góc liên kết OSO gần bằng 120
Cho hai vectơ \(\overrightarrow i ,\overrightarrow j \) vuông góc có cùng độ dài bằng 1.
a) Tính \({\left( {\overrightarrow i + \overrightarrow j } \right)^2};{\left( {\overrightarrow i - \overrightarrow j } \right)^2};\left( {\overrightarrow i + \overrightarrow j } \right)\left( {\overrightarrow i - \overrightarrow j } \right)\).
b) Cho \(\overrightarrow a = 2\overrightarrow i + 2\overrightarrow j ,\overrightarrow b = 3\overrightarrow i - 3\overrightarrow j \). Tính tích vô hướng \(\overrightarrow a .\overrightarrow b \) và tính góc \(\left( {\overrightarrow a ,\overrightarrow b } \right)\)
Phương pháp giải:
Sử dụng các tính chất của tích vô hướng giữa các vectơ
Lời giải chi tiết:
a) Ta có hai vectơ \(\overrightarrow i \) và \(\overrightarrow j \) vuông góc nên \(\overrightarrow i .\overrightarrow j = 0\)
+) \({\left( {\overrightarrow i + \overrightarrow j } \right)^2} = {\left( {\overrightarrow i } \right)^2} + {\left( {\overrightarrow j } \right)^2} + 2\overrightarrow i .\overrightarrow j = {\left| {\overrightarrow i } \right|^2} + {\left| {\overrightarrow j } \right|^2} = 1 + 1 = 2\)
+) \({\left( {\overrightarrow i + \overrightarrow j } \right)^2} = {\left( {\overrightarrow i } \right)^2} + {\left( {\overrightarrow j } \right)^2} - 2\overrightarrow i .\overrightarrow j = {\left| {\overrightarrow i } \right|^2} + {\left| {\overrightarrow j } \right|^2} = 1 + 1 = 2\)
+) \(\left( {\overrightarrow i + \overrightarrow j } \right)\left( {\overrightarrow i - \overrightarrow j } \right) = {\left( {\overrightarrow i } \right)^2} - {\left( {\overrightarrow j } \right)^2} = {\left| {\overrightarrow i } \right|^2} - {\left| {\overrightarrow j } \right|^2} = 1 - 1 = 0\)
b) Sử dụng kết quả của câu a) ta có:
\(\overrightarrow a .\overrightarrow b = \left( {2\overrightarrow i + 2\overrightarrow j } \right).\left( {3\overrightarrow i - 3\overrightarrow j } \right) = 2.3.\left( {\overrightarrow i + \overrightarrow j } \right).\left( {\overrightarrow i - \overrightarrow j } \right) = 6.0 = 0\)
\(\overrightarrow a .\overrightarrow b = 0 \Rightarrow \overrightarrow a \bot \overrightarrow b \Rightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = 90^\circ \)
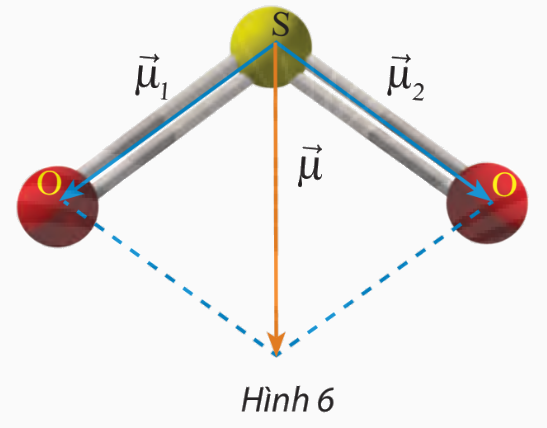
Phân tử sulfur dioxide \((S{O_2})\) có cấu tạo hình chữ V, góc liên kết \(\widehat {OSO}\) gần bằng \(120^\circ \). Người ta biểu diễn sự phân cực giữa nguyên tử S và nguyên tử O bằng các vectơ \(\overrightarrow {{\mu _1}} \)và \(\overrightarrow {{\mu _2}} \) có cùng phương với liên kết cộng hóa trị, có chiều từ nguyên tử S về mỗi nguyên tử O và có độ dài là 1,6 đơn vị (Hình 6). Cho biết vectơ tổng\(\overrightarrow \mu = \overrightarrow {{\mu _1}} + \overrightarrow {{\mu _2}} \) được dùng để biểu diễn sự phân cực của cả phân tử \(\)SO2. Tính độ dài của \(\overrightarrow \mu \).
Phương pháp giải:
Sử dụng kết quả của ví dụ 4 trang 101 \({c^2} = {a^2} + {b^2} - 2bc.\cos C\)
Lời giải chi tiết:
Từ điểm cuối của vectơ \(\overrightarrow {{\mu _1}} \) vẽ vectơ \(\overrightarrow {{\mu _3}} = \overrightarrow {{\mu _2}} \)
Suy ra \(\overrightarrow \mu = \overrightarrow {{\mu _1}} + \overrightarrow {{\mu _2}} = \overrightarrow {{\mu _1}} + \overrightarrow {{\mu _3}} \Rightarrow \left| {\overrightarrow \mu } \right| = \left| {\overrightarrow {{\mu _1}} + \overrightarrow {{\mu _3}} } \right|\)
Ta có: \(\left( {\overrightarrow {{\mu _1}} ,\overrightarrow {{\mu _2}} } \right) = 120^\circ \Rightarrow \left( {\overrightarrow {{\mu _1}} ,\overrightarrow {{\mu _3}} } \right) = 60^\circ \)
\( \Rightarrow {\left| {\overrightarrow \mu } \right|^2} = {\left| {\overrightarrow {{\mu _1}} } \right|^2} + {\left| {\overrightarrow {{\mu _3}} } \right|^2} - 2\left| {\overrightarrow {{\mu _1}} } \right|\left| {\overrightarrow {{\mu _3}} } \right|\cos \left( {\overrightarrow {{\mu _1}} ,\overrightarrow {{\mu _3}} } \right)\)
\( = 1,{6^2} + 1,{6^2} - 2.1,6.1,6.\cos 60^\circ = \frac{{64}}{{25}}\)
\( \Rightarrow \left| {\overrightarrow \mu } \right| = \sqrt {\frac{{64}}{{25}}} = 1,6\)
Vậy độ dài của \(\overrightarrow \mu \) là 1,6 đơn vị
Cho hai vectơ \(\overrightarrow i ,\overrightarrow j \) vuông góc có cùng độ dài bằng 1.
a) Tính \({\left( {\overrightarrow i + \overrightarrow j } \right)^2};{\left( {\overrightarrow i - \overrightarrow j } \right)^2};\left( {\overrightarrow i + \overrightarrow j } \right)\left( {\overrightarrow i - \overrightarrow j } \right)\).
b) Cho \(\overrightarrow a = 2\overrightarrow i + 2\overrightarrow j ,\overrightarrow b = 3\overrightarrow i - 3\overrightarrow j \). Tính tích vô hướng \(\overrightarrow a .\overrightarrow b \) và tính góc \(\left( {\overrightarrow a ,\overrightarrow b } \right)\)
Phương pháp giải:
Sử dụng các tính chất của tích vô hướng giữa các vectơ
Lời giải chi tiết:
a) Ta có hai vectơ \(\overrightarrow i \) và \(\overrightarrow j \) vuông góc nên \(\overrightarrow i .\overrightarrow j = 0\)
+) \({\left( {\overrightarrow i + \overrightarrow j } \right)^2} = {\left( {\overrightarrow i } \right)^2} + {\left( {\overrightarrow j } \right)^2} + 2\overrightarrow i .\overrightarrow j = {\left| {\overrightarrow i } \right|^2} + {\left| {\overrightarrow j } \right|^2} = 1 + 1 = 2\)
+) \({\left( {\overrightarrow i + \overrightarrow j } \right)^2} = {\left( {\overrightarrow i } \right)^2} + {\left( {\overrightarrow j } \right)^2} - 2\overrightarrow i .\overrightarrow j = {\left| {\overrightarrow i } \right|^2} + {\left| {\overrightarrow j } \right|^2} = 1 + 1 = 2\)
+) \(\left( {\overrightarrow i + \overrightarrow j } \right)\left( {\overrightarrow i - \overrightarrow j } \right) = {\left( {\overrightarrow i } \right)^2} - {\left( {\overrightarrow j } \right)^2} = {\left| {\overrightarrow i } \right|^2} - {\left| {\overrightarrow j } \right|^2} = 1 - 1 = 0\)
b) Sử dụng kết quả của câu a) ta có:
\(\overrightarrow a .\overrightarrow b = \left( {2\overrightarrow i + 2\overrightarrow j } \right).\left( {3\overrightarrow i - 3\overrightarrow j } \right) = 2.3.\left( {\overrightarrow i + \overrightarrow j } \right).\left( {\overrightarrow i - \overrightarrow j } \right) = 6.0 = 0\)
\(\overrightarrow a .\overrightarrow b = 0 \Rightarrow \overrightarrow a \bot \overrightarrow b \Rightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = 90^\circ \)
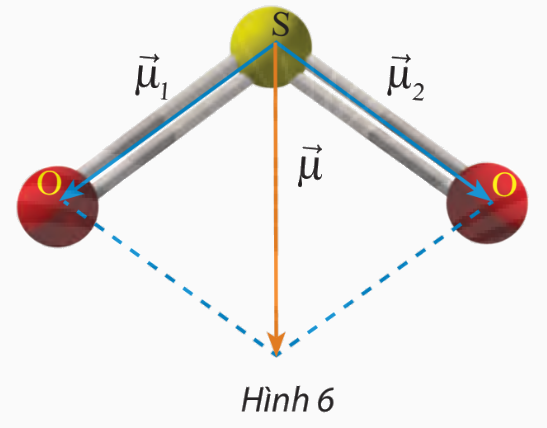
Phân tử sulfur dioxide \((S{O_2})\) có cấu tạo hình chữ V, góc liên kết \(\widehat {OSO}\) gần bằng \(120^\circ \). Người ta biểu diễn sự phân cực giữa nguyên tử S và nguyên tử O bằng các vectơ \(\overrightarrow {{\mu _1}} \)và \(\overrightarrow {{\mu _2}} \) có cùng phương với liên kết cộng hóa trị, có chiều từ nguyên tử S về mỗi nguyên tử O và có độ dài là 1,6 đơn vị (Hình 6). Cho biết vectơ tổng\(\overrightarrow \mu = \overrightarrow {{\mu _1}} + \overrightarrow {{\mu _2}} \) được dùng để biểu diễn sự phân cực của cả phân tử \(\)SO2. Tính độ dài của \(\overrightarrow \mu \).
Phương pháp giải:
Sử dụng kết quả của ví dụ 4 trang 101 \({c^2} = {a^2} + {b^2} - 2bc.\cos C\)
Lời giải chi tiết:
Từ điểm cuối của vectơ \(\overrightarrow {{\mu _1}} \) vẽ vectơ \(\overrightarrow {{\mu _3}} = \overrightarrow {{\mu _2}} \)
Suy ra \(\overrightarrow \mu = \overrightarrow {{\mu _1}} + \overrightarrow {{\mu _2}} = \overrightarrow {{\mu _1}} + \overrightarrow {{\mu _3}} \Rightarrow \left| {\overrightarrow \mu } \right| = \left| {\overrightarrow {{\mu _1}} + \overrightarrow {{\mu _3}} } \right|\)
Ta có: \(\left( {\overrightarrow {{\mu _1}} ,\overrightarrow {{\mu _2}} } \right) = 120^\circ \Rightarrow \left( {\overrightarrow {{\mu _1}} ,\overrightarrow {{\mu _3}} } \right) = 60^\circ \)
\( \Rightarrow {\left| {\overrightarrow \mu } \right|^2} = {\left| {\overrightarrow {{\mu _1}} } \right|^2} + {\left| {\overrightarrow {{\mu _3}} } \right|^2} - 2\left| {\overrightarrow {{\mu _1}} } \right|\left| {\overrightarrow {{\mu _3}} } \right|\cos \left( {\overrightarrow {{\mu _1}} ,\overrightarrow {{\mu _3}} } \right)\)
\( = 1,{6^2} + 1,{6^2} - 2.1,6.1,6.\cos 60^\circ = \frac{{64}}{{25}}\)
\( \Rightarrow \left| {\overrightarrow \mu } \right| = \sqrt {\frac{{64}}{{25}}} = 1,6\)
Vậy độ dài của \(\overrightarrow \mu \) là 1,6 đơn vị
Mục 3 trong SGK Toán 10 tập 1 chương trình Chân trời sáng tạo tập trung vào việc ứng dụng kiến thức về vectơ trong hình học. Cụ thể, các em sẽ được làm quen với các khái niệm như tích vô hướng của hai vectơ, góc giữa hai vectơ, và các ứng dụng của chúng trong việc giải quyết các bài toán liên quan đến hình học phẳng.
Bài tập mục 3 trang 100, 101 SGK Toán 10 tập 1 Chân trời sáng tạo bao gồm các dạng bài tập khác nhau, đòi hỏi học sinh phải vận dụng linh hoạt các kiến thức đã học. Dưới đây là phân tích chi tiết từng bài tập:
Bài tập này yêu cầu học sinh tính tích vô hướng của hai vectơ cho trước. Để giải bài tập này, các em cần nắm vững công thức tính tích vô hướng: a.b = |a||b|cos(θ), trong đó θ là góc giữa hai vectơ a và b.
Bài tập này yêu cầu học sinh xác định góc giữa hai vectơ. Các em có thể sử dụng công thức sau để tính góc θ: cos(θ) = (a.b) / (|a||b|). Sau khi tính được cos(θ), các em có thể sử dụng máy tính để tìm ra giá trị của θ.
Bài tập này yêu cầu học sinh sử dụng tích vô hướng để chứng minh hai vectơ vuông góc. Hai vectơ a và b vuông góc khi và chỉ khi tích vô hướng của chúng bằng 0: a.b = 0.
Ví dụ: Cho hai vectơ a = (1; 2) và b = (-3; 1). Tính tích vô hướng của hai vectơ này.
Giải: Tích vô hướng của hai vectơ a và b được tính như sau:
a.b = (1)(-3) + (2)(1) = -3 + 2 = -1
Hy vọng với những hướng dẫn chi tiết trên, các em học sinh đã có thể tự tin giải quyết các bài tập mục 3 trang 100, 101 SGK Toán 10 tập 1 chương trình Chân trời sáng tạo. Chúc các em học tập tốt và đạt kết quả cao!
| Công thức | Mô tả |
|---|---|
| a.b = |a||b|cos(θ) | Tích vô hướng của hai vectơ |
| cos(θ) = (a.b) / (|a||b|) | Tính góc giữa hai vectơ |
| a.b = 0 | Điều kiện hai vectơ vuông góc |