Chào mừng bạn đến với bài học lý thuyết về Hệ bất phương trình bậc nhất hai ẩn trong chương trình Toán 10 Chân trời sáng tạo tại giaitoan.edu.vn. Bài viết này sẽ cung cấp kiến thức nền tảng, các định nghĩa, tính chất và phương pháp giải hệ bất phương trình một cách chi tiết và dễ hiểu.
Chúng tôi cam kết mang đến cho bạn trải nghiệm học toán online hiệu quả, với nội dung được trình bày rõ ràng, logic và có nhiều ví dụ minh họa.
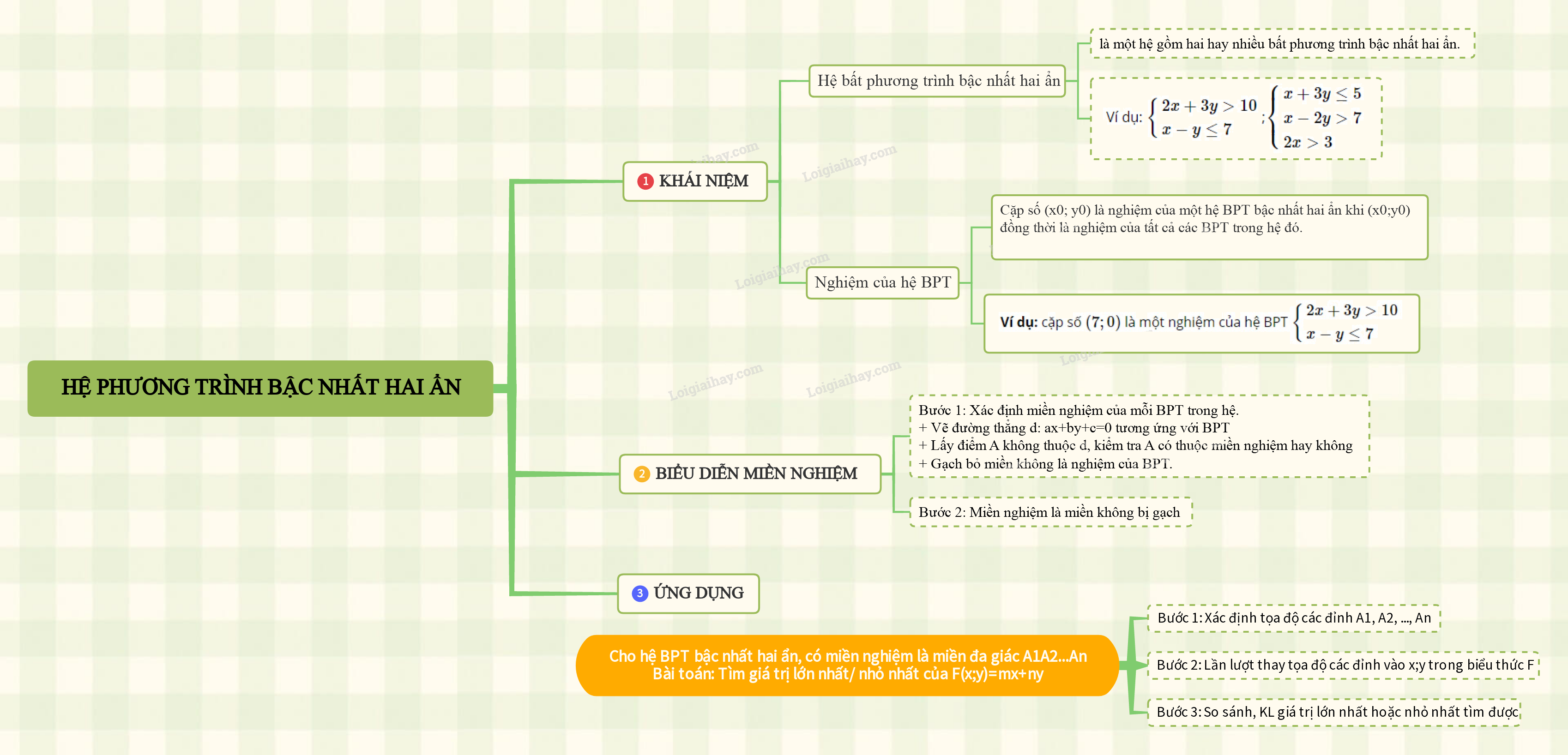
1. Khái niệm hệ bất phương trình bậc nhất hai ẩn 2. Biểu diễn miền nghiệm của hệ bất phương trình bậc nhất hai ẩn trên mặt phẳng tọa độ 3. Tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của biểu thức F = ax + by trên một miền đa giác
1. Khái niệm hệ bất phương trình bậc nhất hai ẩn
+) Hệ bất phương trình bậc nhất hai ẩn là một hệ gồm hai hay nhiều bất phương trình bậc nhất hai ẩn.
Ví dụ: \(\left\{ \begin{array}{l}2x + 3y > 10\\x - y \le 7\end{array} \right.\);\(\left\{ \begin{array}{l}x + 3y \le 5\\x - 2y > 7\\2x > 3\end{array} \right.\)
+) Cặp số \(({x_0};{y_0})\) là nghiệm của một hệ BPT bậc nhất hai ẩn khi \(({x_0};{y_0})\) đồng thời là nghiệm của tất cả các BPT trong hệ đó.
Ví dụ: cặp số \((7;0)\) là một nghiệm của hệ BPT \(\left\{ \begin{array}{l}2x + 3y > 10\\x - y \le 7\end{array} \right.\)
2. Biểu diễn miền nghiệm của hệ bất phương trình bậc nhất hai ẩn trên mặt phẳng tọa độ
+) Trong mặt phẳng tọa độ Oxy, tập hợp các điểm có tọa độ là nghiệm của hệ bất phương trình bậc nhất hai ẩn là miền nghiệm của hệ BPT đó.
+) Miền nghiệm của hệ là giao các miền nghiệm của các bất phương trình trong hệ.
+) Biểu diễn miền nghiệm của một hệ BPT bậc nhất hai ẩn:
Bước 1: Trên cùng một mặt phẳng tọa độ, biểu diễn miền nghiệm của mỗi bất phương trình của hệ.
Bước 2: Phần giao của các miền nghiệm là miền nghiệm của hệ BPT.
3. Tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của biểu thức F = ax + by trên một miền đa giác
Cho hệ BPT bậc nhất hai ẩn x, y có miền nghiệm là miền đa giác \({A_1}{A_2}...{A_n}\).
Khi đó: Giá trị lớn nhất (hay nhỏ nhất) của biể thức \(F(x;y) = mx + ny\), với \((x;y)\) là tọa độ các điểm thuộc miền đa giác \({A_1}{A_2}...{A_n}\), đạt được tại một trong các đỉnh của đa giác đó.
Hệ bất phương trình bậc nhất hai ẩn là một tập hợp các bất phương trình bậc nhất hai ẩn được xét đồng thời. Việc giải hệ bất phương trình này giúp xác định miền nghiệm, tức là tập hợp tất cả các cặp số (x, y) thỏa mãn tất cả các bất phương trình trong hệ.
Hệ bất phương trình bậc nhất hai ẩn có dạng:
Trong đó, a1, b1, c1, a2, b2, c2 là các số thực và a1, b1, a2, b2 không đồng thời bằng 0.
Miền nghiệm của hệ bất phương trình là tập hợp tất cả các điểm (x, y) trên mặt phẳng tọa độ thỏa mãn đồng thời tất cả các bất phương trình trong hệ. Để biểu diễn miền nghiệm, ta thường vẽ các đường thẳng tương ứng với các bất phương trình và xác định phần mặt phẳng thỏa mãn các điều kiện bất đẳng thức.
Để giải hệ bất phương trình bậc nhất hai ẩn, ta thực hiện các bước sau:
Xét hệ bất phương trình sau:
Bước 1: Vẽ đường thẳng x + y = 2 và x - y = 0.
Bước 2: Xác định miền nghiệm của mỗi bất phương trình.
Bước 3: Tìm giao của hai miền nghiệm. Giao này là miền nghiệm của hệ bất phương trình.
Hệ bất phương trình bậc nhất hai ẩn có nhiều ứng dụng trong thực tế, ví dụ như:
Để củng cố kiến thức về hệ bất phương trình bậc nhất hai ẩn, bạn có thể thực hành giải các bài tập sau:
Hệ bất phương trình bậc nhất hai ẩn là một công cụ quan trọng trong toán học và có nhiều ứng dụng trong thực tế. Việc nắm vững lý thuyết và phương pháp giải hệ bất phương trình này sẽ giúp bạn giải quyết nhiều bài toán khác nhau một cách hiệu quả.