Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các câu hỏi trong sách giáo khoa Toán 10 tập 1, trang 133, chương trình Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong học tập.
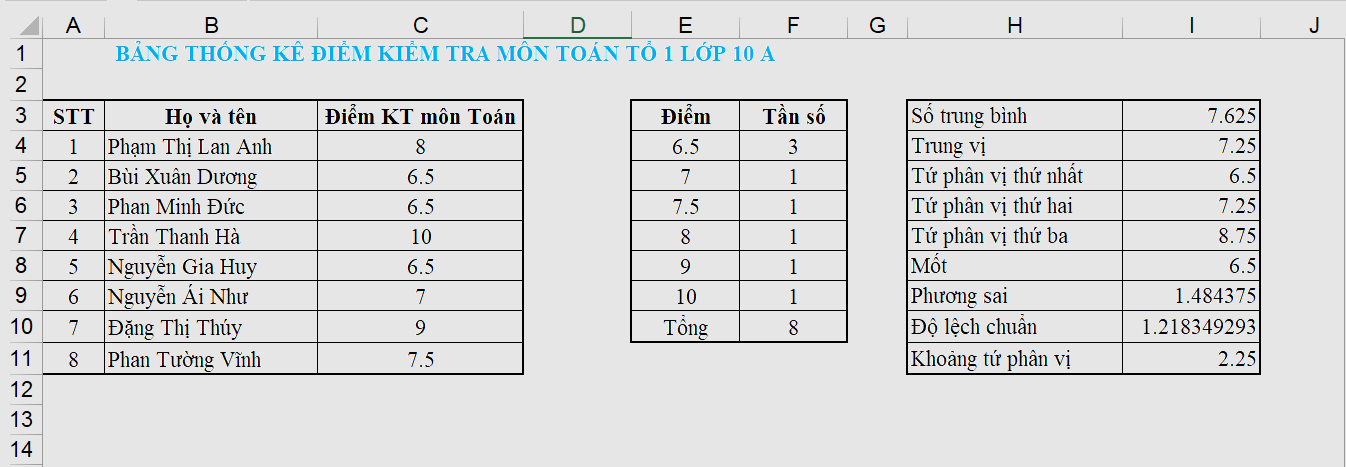
Chia lớp theo tổ để phân công làm thống kê như trên đối với điểm kiểm tra môn Toán của lớp và tổng hợp các kết quả trong một văn bản hoặc trang trình chiếu. Làm tương tự với điểm kiểm tra các môn học khác của lớp
Chia lớp theo tổ để phân công làm thống kê như trên đối với điểm kiểm tra môn Toán của lớp và tổng hợp các kết quả trong một văn bản hoặc trang trình chiếu.
Lời giải chi tiết:
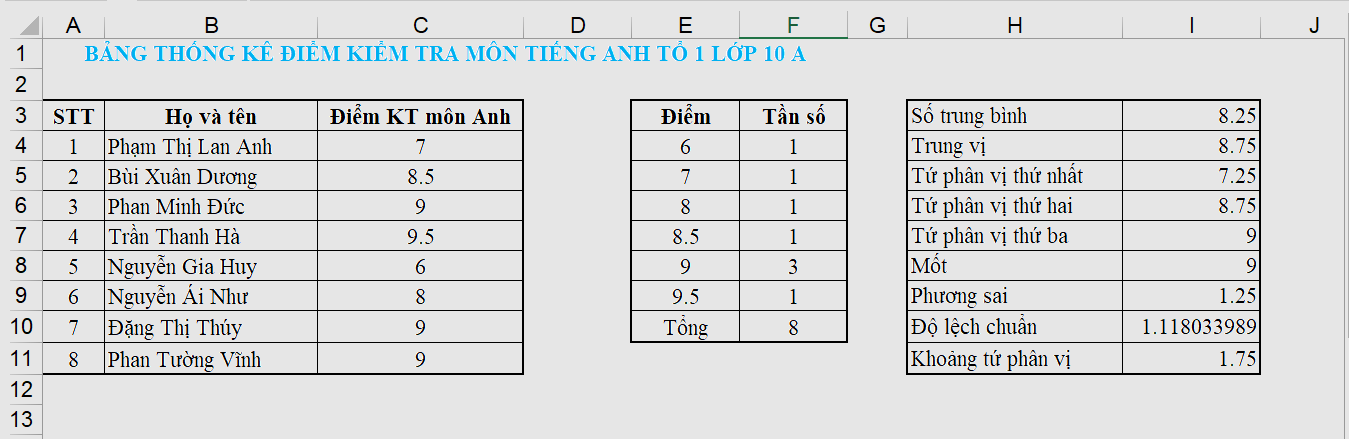
Làm tương tự với điểm kiểm tra các môn học khác của lớp
Lời giải chi tiết:
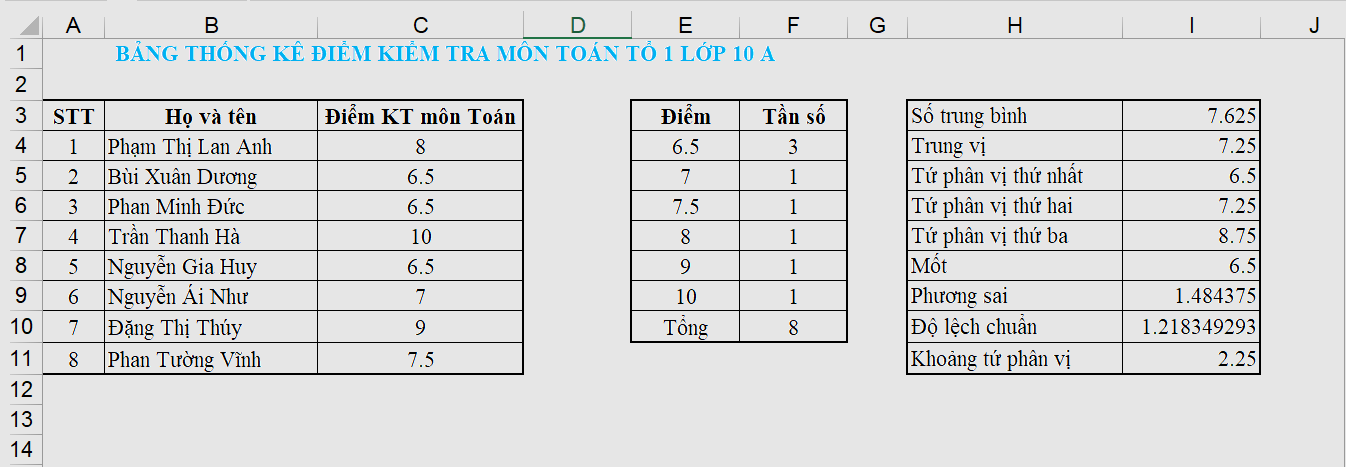
Chia lớp theo tổ để phân công làm thống kê như trên đối với điểm kiểm tra môn Toán của lớp và tổng hợp các kết quả trong một văn bản hoặc trang trình chiếu.
Lời giải chi tiết:
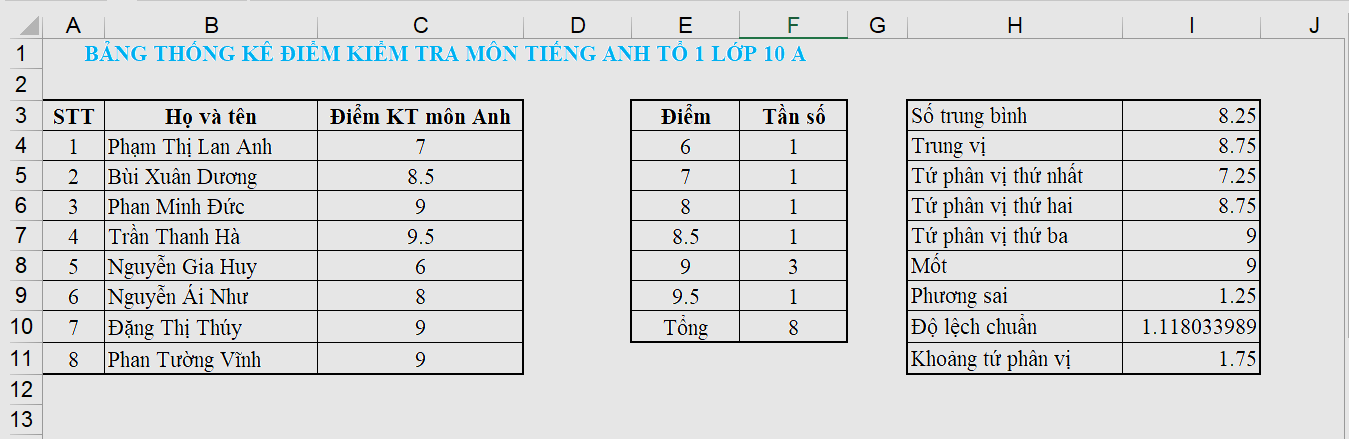
Làm tương tự với điểm kiểm tra các môn học khác của lớp
Lời giải chi tiết:
Bài tập trang 133 SGK Toán 10 tập 1 Chân trời sáng tạo tập trung vào việc vận dụng các kiến thức về vectơ, phép toán vectơ, và các tính chất liên quan để giải quyết các bài toán hình học và đại số cơ bản. Dưới đây là lời giải chi tiết cho từng bài tập:
Để hai vectơ a và b cùng phương, phải tồn tại một số thực k sao cho a = kb.
Chứng minh:
Chứng minh:
Vì ABCD là hình bình hành, nên O là trung điểm của AC và BD.
Do đó, OA = OC và OB = OD.
Suy ra OA + OB = OC + OD. (ĐPCM)
(a) A, B, C, D là bốn đỉnh của một hình bình hành.
(b) A, B, C, D là bốn điểm nằm trên một đường thẳng theo thứ tự đó.
Giải:
(a) Nếu A, B, C, D là bốn đỉnh của một hình bình hành, thì AB = DC. Do đó, AB + CD = DC + CD = 2CD.
(b) Nếu A, B, C, D là bốn điểm nằm trên một đường thẳng theo thứ tự đó, thì AB + CD = AD.
Hy vọng với lời giải chi tiết này, các em sẽ hiểu rõ hơn về các khái niệm và kỹ năng giải toán liên quan đến vectơ. Chúc các em học tập tốt!