Bài 6 trang 71 SGK Toán 10 tập 2 thuộc chương trình Toán 10 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về vectơ và ứng dụng của vectơ trong hình học. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 6 trang 71 SGK Toán 10 tập 2, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
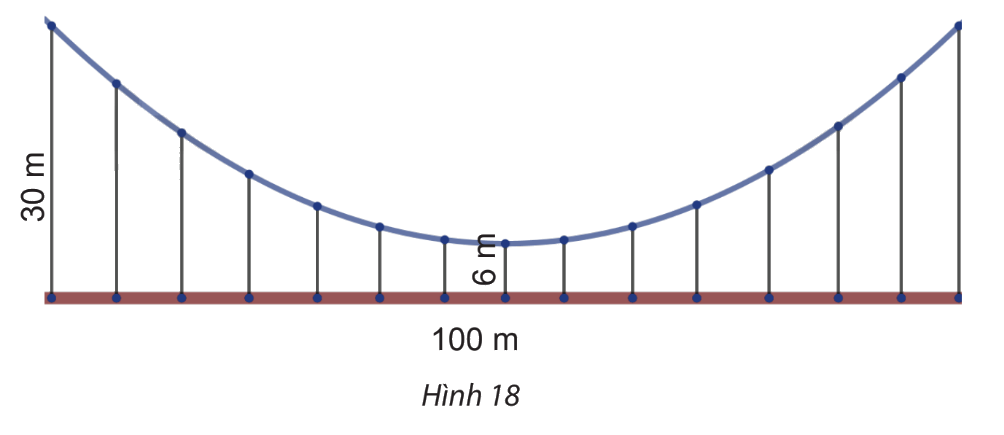
Một cái cầu có dây cáp treo như hình vẽ parabol, cầu dài 100 m và được nâng đỡ bởi những thanh thẳng đứng treo từ cáp xuống, thanh dài nhất là 30m, thanh ngắn nhất là 6m (hình 18). Tính chiều dài của thanh cách điểm giữa cầu 18m
Đề bài
Một cái cầu có dây cáp treo như hình vẽ parabol, cầu dài 100 m và được nâng đỡ bởi những thanh thẳng đứng treo từ cáp xuống, thanh dài nhất là 30m, thanh ngắn nhất là 6m (hình 18). Tính chiều dài của thanh cách điểm giữa cầu 18m
Phương pháp giải - Xem chi tiết
Bước 1: Gắn hệ trục tọa độ với gốc tọa độ tại điểm giữa cầu
Bước 2: Xác định phương trình mô tả hình dạng của cầu
Bước 3: Thay giả thiết vào phương trình vừa tìm được để tìm chiều dài thanh treo cầu
Lời giải chi tiết
Chọn hệ tọa độ Oxy với gốc tọa độ tại điểm trên của thanh ngắn giữa cầu, trục tung tương ứng là mặt đường của cầu, vẽ lại hình như dưới đây
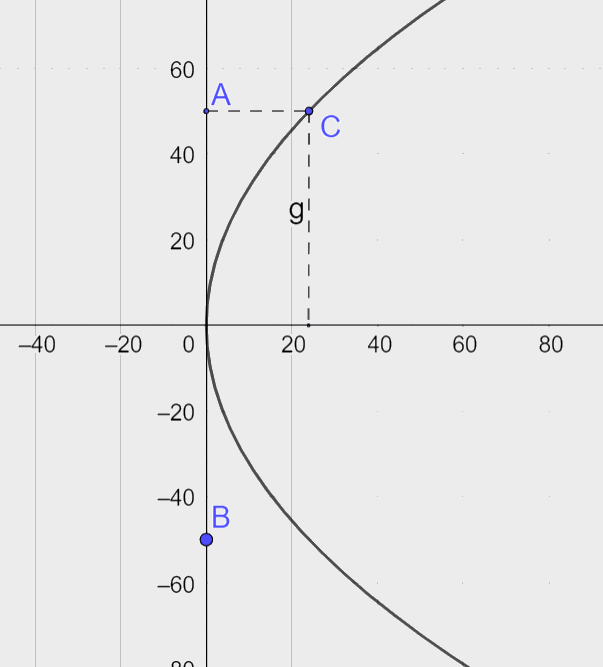
Ta nhận thấy cầu có dạng parabol nên gọi phương trình mô tả hình dạng cầu là \({y^2} = 2px\)
Cầu dài 100 m tương ứng \(AB = 2OB = 100 \Rightarrow OB = 50\), thanh dài nhất dài 30 m
Từ đó ta có tọa độ điểm \(C(24;50)\)
Thay tọa độ C vào phương trình \({y^2} = 2px\) ta có \(2500 = 2p.24 \Rightarrow p = \frac{{625}}{{12}}\)
Ta có phương trình mô tả cây cầu là \({y^2} = \frac{{625}}{6}x\)
Tại thanh cách điểm giữa cầu 18m thì \(x = 18\) ta có \({18^2} = \frac{{625}}{6}.x \Rightarrow x \approx 3,11\)
Do thanh ngắn nhất là 6m nên chiều dài của thanh cách điểm giữa cầu 18m là x + 6 = 3,11+ 6 = 9,11 (m).
Vậy chiều dài của thanh cách điểm giữa cầu 18m gần bằng 9,11 m.
Bài 6 trang 71 SGK Toán 10 tập 2 – Chân trời sáng tạo thường xoay quanh việc áp dụng các tính chất của vectơ, đặc biệt là các phép toán cộng, trừ vectơ, tích của một số với vectơ, và các ứng dụng trong hình học phẳng. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản và các định lý liên quan.
Bài 6 thường bao gồm các dạng bài tập sau:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài 6 trang 71 SGK Toán 10 tập 2, chúng ta sẽ đi vào giải chi tiết từng phần của bài tập. (Nội dung giải chi tiết sẽ được trình bày ở đây, bao gồm các bước giải, giải thích rõ ràng, và các lưu ý quan trọng. Ví dụ:)
Cho tam giác ABC. Gọi M là trung điểm của BC. Chứng minh rằng: overrightarrow{AM} = (overrightarrow{AB} +overrightarrow{AC})/2
Giải:
Để giải các bài tập về vectơ một cách hiệu quả, các em học sinh nên:
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập về vectơ, các em học sinh có thể tham khảo các bài tập sau:
Bài 6 trang 71 SGK Toán 10 tập 2 – Chân trời sáng tạo là một bài tập quan trọng giúp học sinh nắm vững kiến thức về vectơ và ứng dụng của vectơ trong hình học. Hy vọng với lời giải chi tiết và các mẹo giải bài tập mà Giaitoan.edu.vn cung cấp, các em học sinh sẽ tự tin giải quyết bài tập này và đạt kết quả tốt trong môn Toán 10.
| Khái niệm | Định nghĩa |
|---|---|
| Vectơ | Một đoạn thẳng có hướng. |
| Phép cộng vectơ | Quy tắc hình bình hành. |