Chào mừng bạn đến với bài học về Lý thuyết Dấu của tam thức bậc hai, một phần quan trọng trong chương trình Toán 10 Chân trời sáng tạo. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và cần thiết để hiểu rõ về dấu của tam thức bậc hai, một công cụ hữu ích trong việc giải quyết các bài toán liên quan đến bất phương trình bậc hai.
Tại giaitoan.edu.vn, chúng tôi cam kết mang đến cho bạn những bài giảng chất lượng, dễ hiểu và đầy đủ, giúp bạn tự tin chinh phục môn Toán.
A. Lý thuyết 1. Tam thức bậc hai
A. Lý thuyết
1. Tam thức bậc hai
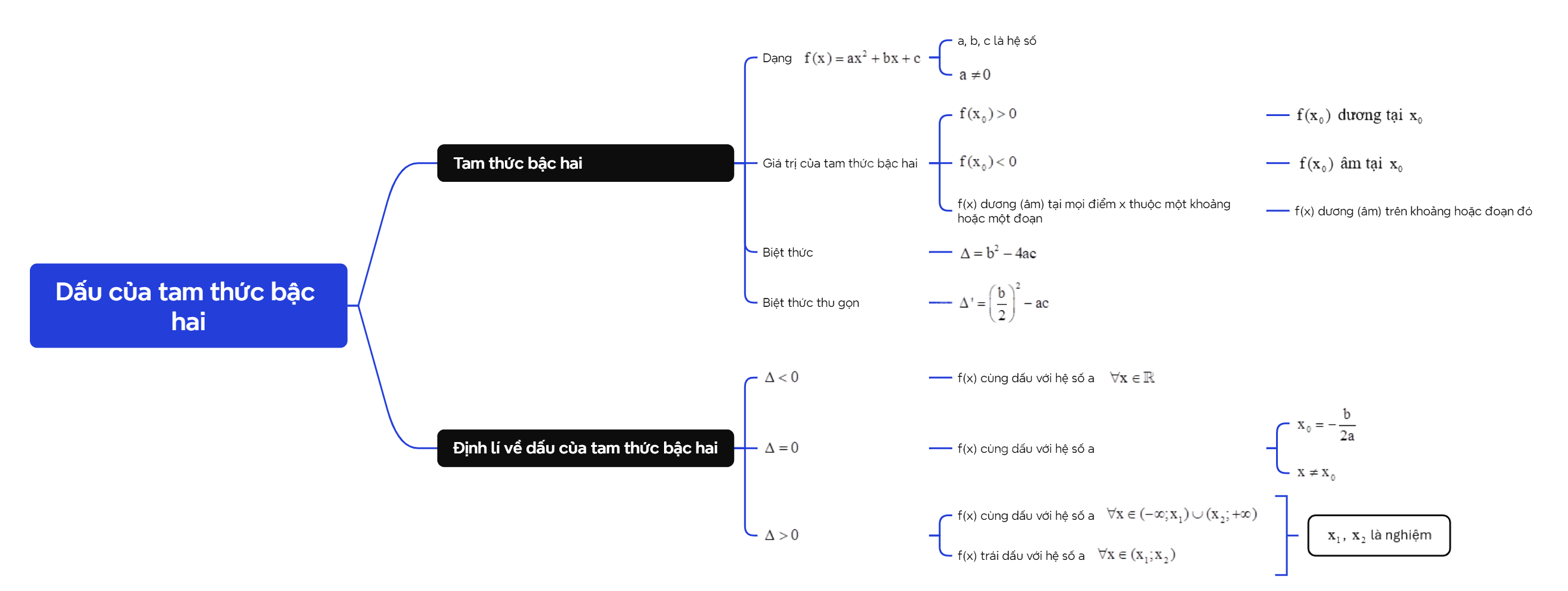
| Đa thức bậc hai \(f(x) = a{x^2} + bx + c\) với a, b, c là các hệ số, \(a \ne 0\) và x là biến số được gọi là tam thức bậc hai. |
Khi thay x bằng giá trị \({x_0}\) vào f(x), ta được \(f({x_0}) = a{x_0}^2 + b{x_0} + c\), gọi là giá trị của tam thức bậc hai.
- Nếu \(f({x_0}) > 0\) thì ta nói \(f({x_0})\) dương tại \({x_0}\).
- Nếu \(f({x_0}) < 0\) thì ta nói \(f({x_0})\) âm tại \({x_0}\).
- Nếu f(x) dương (âm) tại mọi điểm x thuộc một khoảng hoặc một đoạn thì ta nói f(x) dương (âm) trên khoảng hoặc đoạn đó.
Cho tam thức bậc hai \(f(x) = a{x^2} + bx + c\) \((a \ne 0)\). Khi đó: - Nghiệm của phương trình bậc hai \(a{x^2} + bx + c = 0\) là nghiệm của f(x). - Biểu thức \(\Delta = {b^2} - 4ac\) và \(\Delta ' = {\left( {\frac{b}{2}} \right)^2} - ac\) lần lượt là biệt thức và biệt thức thu gọn của f(x). |
2. Định lí về dấu của tam thức bậc hai
Mối quan hệ giữa dấu của tam thức bậc hai với dấu của hệ số a trong từng trường hợp của được phát biểu trong định lí về dấu của tam thức bậc hai sau đây:
Cho tam thức bậc hai \(f(x) = a{x^2} + bx + c\) \((a \ne 0)\). - Nếu \(\Delta < 0\) thì f(x) cùng dấu với hệ số a \(\forall x \in \mathbb{R}\). - Nếu \(\Delta = 0\) và \({x_0} = - \frac{b}{{2a}}\) là nghiệm kép của f(x) thì f(x) cùng dấu với hệ số a với mọi \(x \ne {x_0}\). - Nếu \(\Delta > 0\) thì tam thức f(x) có hai nghiệm phân biệt \({x_1}\) và \({x_2}\) \(({x_1} < {x_2})\). Khi đó: + f(x) cùng dấu với hệ số a \(\forall x \in ( - \infty ;{x_1}) \cup ({x_2}; + \infty )\). + f(x) trái dấu với hệ số a \(\forall x \in ({x_1};{x_2})\). |

Chú ý: Để xét dấu tam thức bậc hai \(f(x) = a{x^2} + bx + c\)\((a \ne 0)\), ta thực hiện các bước sau:
B1: Tính và xét dấu của biệt thức \(\Delta \).
B2: Xác định nghiệm của f(x) (nếu có).
B3: Xác định dấu của hệ số a.
B4: Xác định dấu của f(x).
B. Bài tập
Bài 1: Hãy cho biết biểu thức nào sau đây là tam thức bậc hai? Nếu là tam thức bậc hai, hãy xét dấu của nó tại x = 2.
A. \(3x + 2\sqrt x + 1\)
B. \( - 5{x^4} + 3{x^2} + 4\)
C. \( - \frac{2}{3}{x^2} + 7x - 4\)
D. \({\left( {\frac{1}{x}} \right)^2} + 2\frac{1}{x} + 3\)
Giải:
\( - \frac{2}{3}{x^2} + 7x - 4\) là tam thức bậc hai với \(a = - \frac{2}{3},b = 7,c = - 4\).
\(f(2) = - \frac{2}{3}{.2^2} + 7.2 - 4 = \frac{{22}}{3} > 0\) nên f(x) dương tại x = 2.
Bài 2: Xét dấu các tam thức bậc hai sau đây:
a) \({x^2} + x + 1\).
b) \( - \frac{3}{2}{x^2} + 9x - \frac{{27}}{2}\).
c) \(2{x^2} + 6x - 8\).
Giải:
a) \(f(x) = {x^2} + x + 1\) có \(\Delta = - 3 < 0\) và \(a = 1 > 0\) nên f(x) > 0 với mọi \(x \in \mathbb{R}\).
b) \(f(x) = - \frac{3}{2}{x^2} + 9x - \frac{{27}}{2}\) có \(\Delta = 0\) và \(a = - \frac{3}{2} < 0\) nên f(x) có nghiệm kép x = 3 và f(x) < 0 với mọi \(x \ne 3\).
c) Dễ thấy \(f(x) = 2{x^2} + 6x - 8\) có \(\Delta ' = 25 > 0\), a = 2 > 0 và có hai nghiệm phân biệt \({x_1} = - 4\), \({x_2} = 1\). Do đó ta có bảng xét dấu:

Suy ra f(x) > 0 với mọi \(x \in ( - \infty ; - 4) \cup (1; + \infty )\) và f(x) < 0 với mọi \(x \in ( - 4;1)\).
Tam thức bậc hai là một biểu thức toán học quan trọng trong chương trình Toán 10, đặc biệt là khi giải quyết các bài toán về bất phương trình bậc hai. Việc hiểu rõ về dấu của tam thức bậc hai là yếu tố then chốt để xác định nghiệm của bất phương trình và giải quyết các bài toán thực tế.
Tam thức bậc hai là một biểu thức có dạng f(x) = ax2 + bx + c, trong đó a, b, và c là các hệ số thực và a ≠ 0. Dấu của tam thức bậc hai phụ thuộc vào dấu của hệ số a và biệt thức Δ = b2 - 4ac.
Biệt thức Δ đóng vai trò quan trọng trong việc xác định dấu của tam thức bậc hai. Dưới đây là các trường hợp có thể xảy ra:
Ví dụ 1: Xét tam thức bậc hai f(x) = 2x2 - 5x + 2. Ta có a = 2, b = -5, và c = 2. Biệt thức Δ = (-5)2 - 4(2)(2) = 25 - 16 = 9 > 0. Vậy tam thức bậc hai có hai nghiệm phân biệt. Tính nghiệm: x1 = 1/2, x2 = 2. Vì a > 0, f(x) > 0 khi x < 1/2 hoặc x > 2, và f(x) < 0 khi 1/2 < x < 2.
Ví dụ 2: Xét tam thức bậc hai f(x) = -x2 + 4x - 4. Ta có a = -1, b = 4, và c = -4. Biệt thức Δ = 42 - 4(-1)(-4) = 16 - 16 = 0. Vậy tam thức bậc hai có nghiệm kép x0 = 2. Vì a < 0, f(x) ≤ 0 với mọi x ≠ 2.
Lý thuyết dấu của tam thức bậc hai có nhiều ứng dụng trong việc giải quyết các bài toán liên quan đến bất phương trình bậc hai, tìm tập nghiệm của bất phương trình, và xác định khoảng giá trị của biến số.
Hy vọng bài học này đã giúp bạn hiểu rõ hơn về Lý thuyết Dấu của tam thức bậc hai trong chương trình Toán 10 Chân trời sáng tạo. Hãy luyện tập thường xuyên để nắm vững kiến thức và tự tin giải quyết các bài toán liên quan.