Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 tập 2 của giaitoan.edu.vn. Ở đây, chúng tôi cung cấp lời giải chi tiết và dễ hiểu cho tất cả các bài tập trong sách giáo khoa Toán 10 tập 2, chương trình Chân trời sáng tạo.
Mục 3 trang 41, 42, 43, 44 SGK Toán 10 tập 2 tập trung vào các kiến thức về vectơ, các phép toán vectơ và ứng dụng của vectơ trong hình học. Việc nắm vững kiến thức này là nền tảng quan trọng cho các chương trình học toán ở các lớp trên.
Một trò chơi trên máy tính đang mô phỏng một vùng biển có hai hòn đảo nhỏ có tọa độ Trong mặt phẳng Oxy, cho tam giác ABC có tọa độ ba đỉnh a) Tìm tọa độ trung điểm M của cạnh QS b) Tìm tọa độ trọng tâm G của tam giác QRS
Cho hai điểm \(A\left( {{x_A};{y_A}} \right),B\left( {{x_B};{y_B}} \right)\). Từ biểu thức \(\overrightarrow {AB} = \overrightarrow {OB} - \overrightarrow {OA} \), tìm tọa độ vectơ \(\overrightarrow {AB} \) theo tọa độ hai điểm A,B
Phương pháp giải:
Với \(\overrightarrow v = \left( {{v_1};{v_2}} \right),\overrightarrow w = \left( {{w_1};{w_2}} \right)\) thì \(\overrightarrow v + \overrightarrow w \) là \(\left( {{v_1} + {w_1};{v_2} + {w_2}} \right)\)
Lời giải chi tiết:
Ta có tọa độ vectơ \(\overrightarrow {OB} ,\overrightarrow {OA} \) chính là tọa độ điểm B và A
Nên ta có \(\overrightarrow {OB} = \left( {{x_B};{y_B}} \right),\overrightarrow {OA} = \left( {{x_A};{y_A}} \right)\)
\(\overrightarrow {AB} = \overrightarrow {OB} - \overrightarrow {OA} = \left( {{x_B};{y_B}} \right) - \left( {{x_A};{y_A}} \right) = ({x_B} - {x_A};{y_B} - {y_A})\)
Cho \(E\left( {9;9} \right),F\left( {8; - 7} \right),G\left( {0; - 6} \right)\). Tìm tọa độ các vectơ \(\overrightarrow {FE} ,\overrightarrow {FG} ,\overrightarrow {EG} \)
Phương pháp giải:
\(\overrightarrow {AB} = ({x_B} - {x_A};{y_B} - {y_A})\)
Lời giải chi tiết:
Ta có
\(\begin{array}{l}\overrightarrow {FE} = ({x_E} - {x_F};{y_E} - {y_F}) = (9 - 8;9 - ( - 7)) = (1;16)\\\overrightarrow {FG} = ({x_G} - {x_F};{y_G} - {y_F}) = (0 - 8;( - 6) - ( - 7)) = ( - 8;1)\\\overrightarrow {EG} = ({x_G} - {x_E};{y_G} - {y_E}) = (0 - 9;( - 6) - 9) = ( - 9; - 15)\end{array}\)
Trong mặt phẳng Oxy, cho tam giác ABC có tọa độ ba đỉnh là \(A\left( {{x_A};{y_A}} \right),B\left( {{x_B};{y_B}} \right),C\left( {{x_C};{y_C}} \right)\). Gọi \(M\left( {{x_M};{y_M}} \right)\) là trung điểm của đoạn thẳng AB, \(G\left( {{x_G};{y_G}} \right)\) là trọng tâm của tam giác ABC
a) Biểu thị vectơ \(\overrightarrow {OM} \) theo hai vectơ \(\overrightarrow {OA} \) và \(\overrightarrow {OB} \)
b) Biểu thị vectơ \(\overrightarrow {OG} \) theo ba vectơ \(\overrightarrow {OA} \), \(\overrightarrow {OB} \) và \(\overrightarrow {OC} \)
c) Từ các kết quả trên, tìm tọa độ điểm M, G theo tọa độ của các điểm A, B, C
Phương pháp giải:
a) Sử dụng tính chất trung điểm \(\overrightarrow {OM} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right)\) (với M là trung điểm của đoạn thẳng AB)
b) Sử dụng tính chất trọng tâm \(\overrightarrow {OG} = \frac{1}{3}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} } \right)\) (với G là trọng tâm của tam giác ABC)
c) Thay tọa độ các điểm vào và xác định
Lời giải chi tiết:
a) M là trung điểm của đoạn thẳng AB, áp dụng tính chất trung điểm ta có:
\(\overrightarrow {OM} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right)\)
b) G là trọng tâm của tam giác ABC, áp dụng tính chất trọng tâm của tam giác ta có:
\(\overrightarrow {OG} = \frac{1}{3}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} } \right)\)
c) Ta có \(\overrightarrow {OA} = \left( {{x_A};{y_A}} \right),\overrightarrow {OB} = \left( {{x_B};{y_B}} \right),\overrightarrow {OC} = \left( {{x_C};{y_C}} \right)\)
Suy ra:
\(\begin{array}{l}\overrightarrow {OM} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right) = \frac{1}{2}\left[ {\left( {{x_A};{y_A}} \right) + \left( {{x_B};{y_B}} \right)} \right]\\ = \left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)\end{array}\)
\(\begin{array}{l}\overrightarrow {OG} = \frac{1}{3}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} } \right) = \frac{1}{3}\left[ {\left( {{x_A};{y_A}} \right) + \left( {{x_B};{y_B}} \right) + \left( {{x_c};{y_c}} \right)} \right]\\ = \left( {\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3}} \right)\end{array}\)
Mà ta có tọa độ vectơ \(\overrightarrow {OM} \) chính là tọa độ điểm M, nên ta có
Tọa độ điểm M là \(\left( {{x_M};{y_M}} \right) = \left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)\)
Tọa độ điểm G là \(\left( {\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3}} \right)\)
Cho tam giác QRS có tọa độ các đỉnh \(Q\left( {7; - 2} \right),R( - 4;9)\) và \(S(5;8)\).
a) Tìm tọa độ trung điểm M của cạnh QS.
b) Tìm tọa độ trọng tâm G của tam giác QRS.
Phương pháp giải:
Tọa độ điểm M là \(\left( {\frac{{{x_Q} + {x_S}}}{2};\frac{{{y_Q} + {y_S}}}{2}} \right)\).
Tọa độ điểm G là \(\left( {\frac{{{x_Q} + {x_R} + {x_S}}}{3};\frac{{{y_Q} + {y_R} + {y_S}}}{3}} \right)\).
Lời giải chi tiết:
a) \({x_M} = \frac{{{x_Q} + {x_S}}}{2} = \frac{{7 + 5}}{2} = 6; \\{y_M} = \frac{{{y_Q} + {y_S}}}{2} = \frac{{( - 2) + 8}}{2} = 3\).
Vậy \(M\left( {6;3} \right)\).
b)
\({x_G} = \frac{{{x_Q} + {x_S} + {x_R}}}{3} = \frac{{7 + ( - 4) + 5}}{3} = \frac{8}{3};\\{y_M} = \frac{{{y_Q} + {y_S} + {y_R}}}{3} = \frac{{( - 2) + 9 + 8}}{3} = 5\).
Vậy \(G\left( {\frac{8}{3};5} \right)\).
Cho hai vectơ \(\overrightarrow a = ({a_1};{a_2}),\overrightarrow b = ({b_1};{b_2})\) và hai điểm \(A\left( {{x_A};{y_A}} \right),B\left( {{x_B};{y_B}} \right)\). Hoàn thành các phép biến đổi sau:
a) \(\overrightarrow a \bot \overrightarrow b \Leftrightarrow \overrightarrow a .\overrightarrow b = \overrightarrow 0 \Leftrightarrow {a_1}{b_1} + {a_2}{b_2} = ...?\)
b) \(\overrightarrow a \) và \(\overrightarrow b \) cùng phương \( \Leftrightarrow \left\{ \begin{array}{l}{a_1} = t{b_1}\\{a_2} = t{b_2}\end{array} \right.\) hay \(\left\{ \begin{array}{l}{b_1} = k{a_1}\\{b_2} = k{a_2}\end{array} \right. \Leftrightarrow {a_1}{b_2} - {a_2}{b_1} = ...?\)
c) \(\left| {\overrightarrow a } \right| = \sqrt {{{\left( {\overrightarrow a } \right)}^2}} = \sqrt {.?.} \)
d) \(\overrightarrow {AB} = ({x_B} - {x_A};{y_B} - {y_A}) \Rightarrow AB = \sqrt {{{\left( {\overrightarrow {AB} } \right)}^2}} = \sqrt {.?.} \)
e) \(\cos (\overrightarrow a ,\overrightarrow b ) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{{.?.}}{{\sqrt {{a_1}^2 + {a_2}^2} .\sqrt {{b_1}^2 + {b_2}^2} }}\) (\(\overrightarrow a ,\overrightarrow b \) khác \(\overrightarrow 0 \))
Lời giải chi tiết:
a) \(\overrightarrow a \bot \overrightarrow b \Leftrightarrow \overrightarrow a .\overrightarrow b = \overrightarrow 0 \Leftrightarrow {a_1}{b_1} + {a_2}{b_2} = 0\)
b) \(\overrightarrow a \) và \(\overrightarrow b \) cùng phương \( \Leftrightarrow \left\{ \begin{array}{l}{a_1} = t{b_1}\\{a_2} = t{b_2}\end{array} \right.\) hay \(\left\{ \begin{array}{l}{b_1} = k{a_1}\\{b_2} = k{a_2}\end{array} \right.\)
\( \Leftrightarrow {a_1}{b_2} - {a_2}{b_1} = {a_1}.k{a_2} - {a_2}.k{a_1} = 0\)
c) \(\left| {\overrightarrow a } \right| = \sqrt {{{\left( {\overrightarrow a } \right)}^2}} = \sqrt {{a_1}^2 + {a_2}^2} \)
d) \(\overrightarrow {AB} = ({x_B} - {x_A};{y_B} - {y_A}) \Rightarrow AB = \sqrt {{{\left( {\overrightarrow {AB} } \right)}^2}} \)
\( = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2}} \)
e) \(\cos (\overrightarrow a ,\overrightarrow b ) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{{{a_1}{b_1} + {a_2}{b_2}}}{{\sqrt {{a_1}^2 + {a_2}^2} .\sqrt {{b_1}^2 + {b_2}^2} }}\)
Trong mặt phẳng Oxy, cho tam giác DEF có tọa độ các đỉnh \(D(2;2),E(6;2)\) và \(F(2;6)\)
a) Tìm tọa độ điểm H là chân đường vuông cao của tam giác DEF kẻ từ D
b) Giải tam giác DEF
Phương pháp giải:
Bước 1: Tìm tọa độ các vectơ \(\overrightarrow {DH} ,\overrightarrow {EF} \)
Bước 2: Dựa vào ứng dụng tọa độ của các phép toán vectơ (tính chất vuông góc)
Lời giải chi tiết:
a) Ta có: \(\overrightarrow {EF} = \left( { - 2;4} \right)\)
Gọi tọa độ điểm H là \(\left( {x;y} \right)\) ta có \(\overrightarrow {DH} = \left( {x - 2;y - 2} \right),\overrightarrow {EH} = \left( {x - 6;y - 2} \right)\)
H là chân đường cao nên \(\overrightarrow {DH} \bot \overrightarrow {EF} \)
\(\begin{array}{l}\overrightarrow {DH} \bot \overrightarrow {EF} \Leftrightarrow \left( {x - 2} \right).\left( { - 2} \right) + \left( {y - 2} \right).4 = 0\\ \Leftrightarrow - 2x + 4y - 4 = 0\end{array}\) (1)
Hai vectơ \(\overrightarrow {EH} ,\overrightarrow {EF} \) cùng phương
\( \Leftrightarrow \left( {x - 6} \right).( - 2) - \left( {y - 2} \right).4 = 0 \Leftrightarrow - 2x - 4y + 20 = 0\) (2)
Từ (1) và (2) ta có hệ phương trình
\(\left\{ \begin{array}{l} - 2x + 4y - 4 = 0\\ - 2x - 4y + 20 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 4\\y = 3\end{array} \right.\)
Vậy \(H(4;3)\)
b) Ta có: \(\overrightarrow {DE} = (4;0),\overrightarrow {DF} = (0;4),\overrightarrow {EF} = ( - 4;4)\)
Suy ra: \(DE = \left| {\overrightarrow {DE} } \right| = \sqrt {{4^2} + {0^2}} = 4,DF = \left| {\overrightarrow {DF} } \right| = \sqrt {{0^2} + {4^2}} = 4\)
\(EF = \left| {\overrightarrow {EF} } \right| = \sqrt {{{( - 4)}^2} + {4^2}} = 4\sqrt 2 \)
\(\begin{array}{l}\cos D = \cos \left( {\overrightarrow {DE} ,\overrightarrow {DF} } \right) = \frac{{\overrightarrow {DE} .\overrightarrow {DF} }}{{DE.DF}} = \frac{{4.0 + 0.4}}{{4.4}} = 0 \Rightarrow \widehat D = 90^\circ \\\cos E = \cos \left( {\overrightarrow {ED} ,\overrightarrow {EF} } \right) = \frac{{\overrightarrow {ED} .\overrightarrow {EF} }}{{ED.EF}} = \frac{{\left( { - 4} \right).\left( { - 4} \right) + 0.4}}{{4.4\sqrt 2 }} = \frac{{\sqrt 2 }}{2} \Rightarrow \widehat E = 45^\circ \\\widehat F = 180^\circ - \widehat D - \widehat E = 180^\circ - 90^\circ - 45^\circ = 45^\circ \end{array}\)
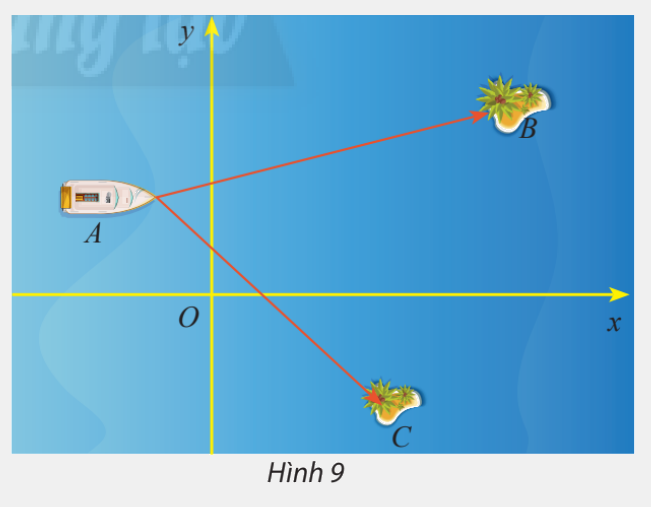
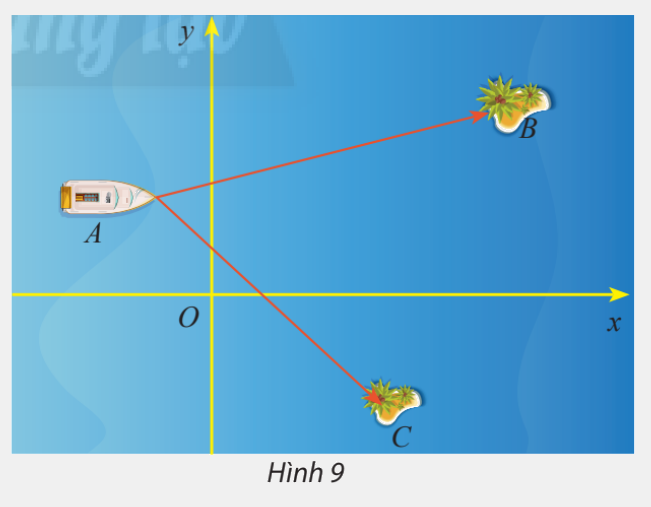
Một trò chơi trên máy tính đang mô phỏng một vùng biển có hai hòn đảo nhỏ có tọa độ \(B\left( {50;30} \right)\) và \(C\left( {32; - 23} \right)\). Một con tàu đang neo đậu tại điểm \(A\left( { - 10;20} \right)\)
a) Tính số đo của \(\widehat {BAC}\)
b) Cho biết một đơn vị trên hệ trục tọa độ tương ứng với 1km. Tính khoảng cách từ con tàu đến mỗi hòn đảo
Phương pháp giải:
Bước 1: Xác định tọa độ các vectơ \(\overrightarrow {AB} ,\overrightarrow {AC} ,\overrightarrow {BC} \)
Bước 2:
a) \(\cos \widehat {BAC} = \cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \frac{{\overrightarrow {AB} .\overrightarrow {AC} }}{{AB.AC}} \)
b) \(AB = \left| {\overrightarrow {AB} } \right| = \sqrt {(x_B - x_A)^2+(y_B-y_A)^2}\)
Lời giải chi tiết:
a) Ta có: \(\overrightarrow {AB} = \left( {60;10} \right),\overrightarrow {AC} = \left( {42; - 43} \right),\overrightarrow {BC} = \left( { - 18; - 53} \right)\)
\(\cos \widehat {BAC} = \cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \frac{{\overrightarrow {AB} .\overrightarrow {AC} }}{{AB.AC}} = \frac{{60.42 + 10.( - 43)}}{{\sqrt {{{60}^2} + {{10}^2}} .\sqrt {{{42}^2} + {{\left( { - 43} \right)}^2}} }} \simeq 0,572 \Rightarrow \widehat {BAC} \approx 55^\circ 8'\)
b)
Khoảng cách từ tàu đến đảo B là \(AB = \left| {\overrightarrow {AB} } \right| = \sqrt {{{60}^2} + {{10}^2}} = 10\sqrt {37} \) (km)
Khoảng cách từ tàu đến đảo B là \(AC = \left| {\overrightarrow {AC} } \right| = \sqrt {{{42}^2} + {{\left( { - 43} \right)}^2}} = \sqrt {3613} \) (km)
Cho hai điểm \(A\left( {{x_A};{y_A}} \right),B\left( {{x_B};{y_B}} \right)\). Từ biểu thức \(\overrightarrow {AB} = \overrightarrow {OB} - \overrightarrow {OA} \), tìm tọa độ vectơ \(\overrightarrow {AB} \) theo tọa độ hai điểm A,B
Phương pháp giải:
Với \(\overrightarrow v = \left( {{v_1};{v_2}} \right),\overrightarrow w = \left( {{w_1};{w_2}} \right)\) thì \(\overrightarrow v + \overrightarrow w \) là \(\left( {{v_1} + {w_1};{v_2} + {w_2}} \right)\)
Lời giải chi tiết:
Ta có tọa độ vectơ \(\overrightarrow {OB} ,\overrightarrow {OA} \) chính là tọa độ điểm B và A
Nên ta có \(\overrightarrow {OB} = \left( {{x_B};{y_B}} \right),\overrightarrow {OA} = \left( {{x_A};{y_A}} \right)\)
\(\overrightarrow {AB} = \overrightarrow {OB} - \overrightarrow {OA} = \left( {{x_B};{y_B}} \right) - \left( {{x_A};{y_A}} \right) = ({x_B} - {x_A};{y_B} - {y_A})\)
Cho \(E\left( {9;9} \right),F\left( {8; - 7} \right),G\left( {0; - 6} \right)\). Tìm tọa độ các vectơ \(\overrightarrow {FE} ,\overrightarrow {FG} ,\overrightarrow {EG} \)
Phương pháp giải:
\(\overrightarrow {AB} = ({x_B} - {x_A};{y_B} - {y_A})\)
Lời giải chi tiết:
Ta có
\(\begin{array}{l}\overrightarrow {FE} = ({x_E} - {x_F};{y_E} - {y_F}) = (9 - 8;9 - ( - 7)) = (1;16)\\\overrightarrow {FG} = ({x_G} - {x_F};{y_G} - {y_F}) = (0 - 8;( - 6) - ( - 7)) = ( - 8;1)\\\overrightarrow {EG} = ({x_G} - {x_E};{y_G} - {y_E}) = (0 - 9;( - 6) - 9) = ( - 9; - 15)\end{array}\)
Trong mặt phẳng Oxy, cho tam giác ABC có tọa độ ba đỉnh là \(A\left( {{x_A};{y_A}} \right),B\left( {{x_B};{y_B}} \right),C\left( {{x_C};{y_C}} \right)\). Gọi \(M\left( {{x_M};{y_M}} \right)\) là trung điểm của đoạn thẳng AB, \(G\left( {{x_G};{y_G}} \right)\) là trọng tâm của tam giác ABC
a) Biểu thị vectơ \(\overrightarrow {OM} \) theo hai vectơ \(\overrightarrow {OA} \) và \(\overrightarrow {OB} \)
b) Biểu thị vectơ \(\overrightarrow {OG} \) theo ba vectơ \(\overrightarrow {OA} \), \(\overrightarrow {OB} \) và \(\overrightarrow {OC} \)
c) Từ các kết quả trên, tìm tọa độ điểm M, G theo tọa độ của các điểm A, B, C
Phương pháp giải:
a) Sử dụng tính chất trung điểm \(\overrightarrow {OM} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right)\) (với M là trung điểm của đoạn thẳng AB)
b) Sử dụng tính chất trọng tâm \(\overrightarrow {OG} = \frac{1}{3}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} } \right)\) (với G là trọng tâm của tam giác ABC)
c) Thay tọa độ các điểm vào và xác định
Lời giải chi tiết:
a) M là trung điểm của đoạn thẳng AB, áp dụng tính chất trung điểm ta có:
\(\overrightarrow {OM} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right)\)
b) G là trọng tâm của tam giác ABC, áp dụng tính chất trọng tâm của tam giác ta có:
\(\overrightarrow {OG} = \frac{1}{3}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} } \right)\)
c) Ta có \(\overrightarrow {OA} = \left( {{x_A};{y_A}} \right),\overrightarrow {OB} = \left( {{x_B};{y_B}} \right),\overrightarrow {OC} = \left( {{x_C};{y_C}} \right)\)
Suy ra:
\(\begin{array}{l}\overrightarrow {OM} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right) = \frac{1}{2}\left[ {\left( {{x_A};{y_A}} \right) + \left( {{x_B};{y_B}} \right)} \right]\\ = \left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)\end{array}\)
\(\begin{array}{l}\overrightarrow {OG} = \frac{1}{3}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} } \right) = \frac{1}{3}\left[ {\left( {{x_A};{y_A}} \right) + \left( {{x_B};{y_B}} \right) + \left( {{x_c};{y_c}} \right)} \right]\\ = \left( {\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3}} \right)\end{array}\)
Mà ta có tọa độ vectơ \(\overrightarrow {OM} \) chính là tọa độ điểm M, nên ta có
Tọa độ điểm M là \(\left( {{x_M};{y_M}} \right) = \left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)\)
Tọa độ điểm G là \(\left( {\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3}} \right)\)
Cho tam giác QRS có tọa độ các đỉnh \(Q\left( {7; - 2} \right),R( - 4;9)\) và \(S(5;8)\).
a) Tìm tọa độ trung điểm M của cạnh QS.
b) Tìm tọa độ trọng tâm G của tam giác QRS.
Phương pháp giải:
Tọa độ điểm M là \(\left( {\frac{{{x_Q} + {x_S}}}{2};\frac{{{y_Q} + {y_S}}}{2}} \right)\).
Tọa độ điểm G là \(\left( {\frac{{{x_Q} + {x_R} + {x_S}}}{3};\frac{{{y_Q} + {y_R} + {y_S}}}{3}} \right)\).
Lời giải chi tiết:
a) \({x_M} = \frac{{{x_Q} + {x_S}}}{2} = \frac{{7 + 5}}{2} = 6; \\{y_M} = \frac{{{y_Q} + {y_S}}}{2} = \frac{{( - 2) + 8}}{2} = 3\).
Vậy \(M\left( {6;3} \right)\).
b)
\({x_G} = \frac{{{x_Q} + {x_S} + {x_R}}}{3} = \frac{{7 + ( - 4) + 5}}{3} = \frac{8}{3};\\{y_M} = \frac{{{y_Q} + {y_S} + {y_R}}}{3} = \frac{{( - 2) + 9 + 8}}{3} = 5\).
Vậy \(G\left( {\frac{8}{3};5} \right)\).
Cho hai vectơ \(\overrightarrow a = ({a_1};{a_2}),\overrightarrow b = ({b_1};{b_2})\) và hai điểm \(A\left( {{x_A};{y_A}} \right),B\left( {{x_B};{y_B}} \right)\). Hoàn thành các phép biến đổi sau:
a) \(\overrightarrow a \bot \overrightarrow b \Leftrightarrow \overrightarrow a .\overrightarrow b = \overrightarrow 0 \Leftrightarrow {a_1}{b_1} + {a_2}{b_2} = ...?\)
b) \(\overrightarrow a \) và \(\overrightarrow b \) cùng phương \( \Leftrightarrow \left\{ \begin{array}{l}{a_1} = t{b_1}\\{a_2} = t{b_2}\end{array} \right.\) hay \(\left\{ \begin{array}{l}{b_1} = k{a_1}\\{b_2} = k{a_2}\end{array} \right. \Leftrightarrow {a_1}{b_2} - {a_2}{b_1} = ...?\)
c) \(\left| {\overrightarrow a } \right| = \sqrt {{{\left( {\overrightarrow a } \right)}^2}} = \sqrt {.?.} \)
d) \(\overrightarrow {AB} = ({x_B} - {x_A};{y_B} - {y_A}) \Rightarrow AB = \sqrt {{{\left( {\overrightarrow {AB} } \right)}^2}} = \sqrt {.?.} \)
e) \(\cos (\overrightarrow a ,\overrightarrow b ) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{{.?.}}{{\sqrt {{a_1}^2 + {a_2}^2} .\sqrt {{b_1}^2 + {b_2}^2} }}\) (\(\overrightarrow a ,\overrightarrow b \) khác \(\overrightarrow 0 \))
Lời giải chi tiết:
a) \(\overrightarrow a \bot \overrightarrow b \Leftrightarrow \overrightarrow a .\overrightarrow b = \overrightarrow 0 \Leftrightarrow {a_1}{b_1} + {a_2}{b_2} = 0\)
b) \(\overrightarrow a \) và \(\overrightarrow b \) cùng phương \( \Leftrightarrow \left\{ \begin{array}{l}{a_1} = t{b_1}\\{a_2} = t{b_2}\end{array} \right.\) hay \(\left\{ \begin{array}{l}{b_1} = k{a_1}\\{b_2} = k{a_2}\end{array} \right.\)
\( \Leftrightarrow {a_1}{b_2} - {a_2}{b_1} = {a_1}.k{a_2} - {a_2}.k{a_1} = 0\)
c) \(\left| {\overrightarrow a } \right| = \sqrt {{{\left( {\overrightarrow a } \right)}^2}} = \sqrt {{a_1}^2 + {a_2}^2} \)
d) \(\overrightarrow {AB} = ({x_B} - {x_A};{y_B} - {y_A}) \Rightarrow AB = \sqrt {{{\left( {\overrightarrow {AB} } \right)}^2}} \)
\( = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2}} \)
e) \(\cos (\overrightarrow a ,\overrightarrow b ) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{{{a_1}{b_1} + {a_2}{b_2}}}{{\sqrt {{a_1}^2 + {a_2}^2} .\sqrt {{b_1}^2 + {b_2}^2} }}\)
Trong mặt phẳng Oxy, cho tam giác DEF có tọa độ các đỉnh \(D(2;2),E(6;2)\) và \(F(2;6)\)
a) Tìm tọa độ điểm H là chân đường vuông cao của tam giác DEF kẻ từ D
b) Giải tam giác DEF
Phương pháp giải:
Bước 1: Tìm tọa độ các vectơ \(\overrightarrow {DH} ,\overrightarrow {EF} \)
Bước 2: Dựa vào ứng dụng tọa độ của các phép toán vectơ (tính chất vuông góc)
Lời giải chi tiết:
a) Ta có: \(\overrightarrow {EF} = \left( { - 2;4} \right)\)
Gọi tọa độ điểm H là \(\left( {x;y} \right)\) ta có \(\overrightarrow {DH} = \left( {x - 2;y - 2} \right),\overrightarrow {EH} = \left( {x - 6;y - 2} \right)\)
H là chân đường cao nên \(\overrightarrow {DH} \bot \overrightarrow {EF} \)
\(\begin{array}{l}\overrightarrow {DH} \bot \overrightarrow {EF} \Leftrightarrow \left( {x - 2} \right).\left( { - 2} \right) + \left( {y - 2} \right).4 = 0\\ \Leftrightarrow - 2x + 4y - 4 = 0\end{array}\) (1)
Hai vectơ \(\overrightarrow {EH} ,\overrightarrow {EF} \) cùng phương
\( \Leftrightarrow \left( {x - 6} \right).( - 2) - \left( {y - 2} \right).4 = 0 \Leftrightarrow - 2x - 4y + 20 = 0\) (2)
Từ (1) và (2) ta có hệ phương trình
\(\left\{ \begin{array}{l} - 2x + 4y - 4 = 0\\ - 2x - 4y + 20 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 4\\y = 3\end{array} \right.\)
Vậy \(H(4;3)\)
b) Ta có: \(\overrightarrow {DE} = (4;0),\overrightarrow {DF} = (0;4),\overrightarrow {EF} = ( - 4;4)\)
Suy ra: \(DE = \left| {\overrightarrow {DE} } \right| = \sqrt {{4^2} + {0^2}} = 4,DF = \left| {\overrightarrow {DF} } \right| = \sqrt {{0^2} + {4^2}} = 4\)
\(EF = \left| {\overrightarrow {EF} } \right| = \sqrt {{{( - 4)}^2} + {4^2}} = 4\sqrt 2 \)
\(\begin{array}{l}\cos D = \cos \left( {\overrightarrow {DE} ,\overrightarrow {DF} } \right) = \frac{{\overrightarrow {DE} .\overrightarrow {DF} }}{{DE.DF}} = \frac{{4.0 + 0.4}}{{4.4}} = 0 \Rightarrow \widehat D = 90^\circ \\\cos E = \cos \left( {\overrightarrow {ED} ,\overrightarrow {EF} } \right) = \frac{{\overrightarrow {ED} .\overrightarrow {EF} }}{{ED.EF}} = \frac{{\left( { - 4} \right).\left( { - 4} \right) + 0.4}}{{4.4\sqrt 2 }} = \frac{{\sqrt 2 }}{2} \Rightarrow \widehat E = 45^\circ \\\widehat F = 180^\circ - \widehat D - \widehat E = 180^\circ - 90^\circ - 45^\circ = 45^\circ \end{array}\)
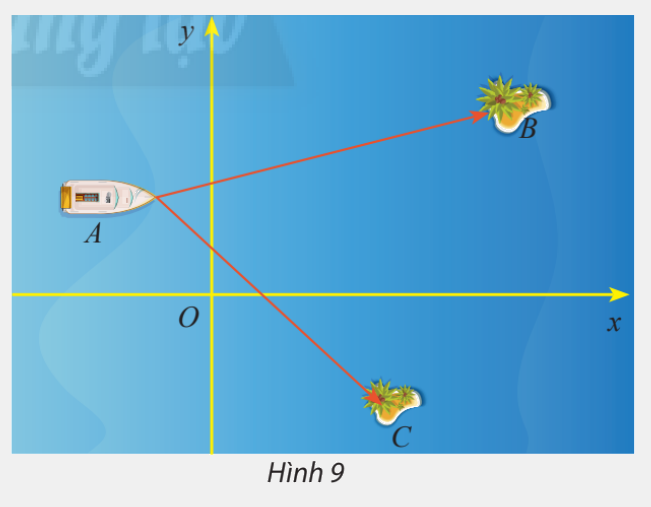
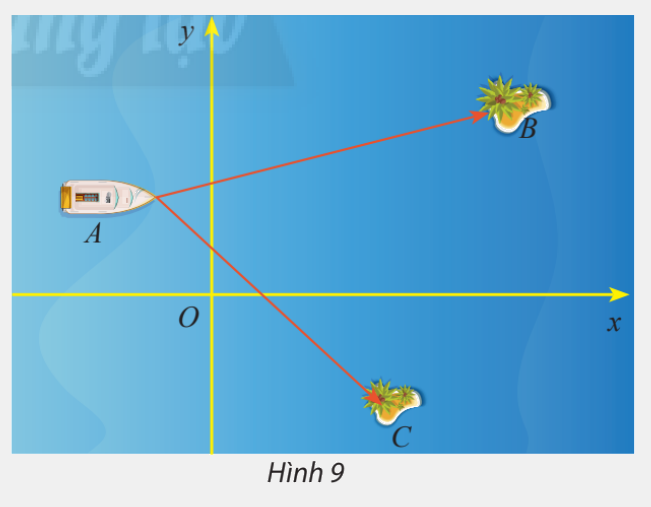
Một trò chơi trên máy tính đang mô phỏng một vùng biển có hai hòn đảo nhỏ có tọa độ \(B\left( {50;30} \right)\) và \(C\left( {32; - 23} \right)\). Một con tàu đang neo đậu tại điểm \(A\left( { - 10;20} \right)\)
a) Tính số đo của \(\widehat {BAC}\)
b) Cho biết một đơn vị trên hệ trục tọa độ tương ứng với 1km. Tính khoảng cách từ con tàu đến mỗi hòn đảo
Phương pháp giải:
Bước 1: Xác định tọa độ các vectơ \(\overrightarrow {AB} ,\overrightarrow {AC} ,\overrightarrow {BC} \)
Bước 2:
a) \(\cos \widehat {BAC} = \cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \frac{{\overrightarrow {AB} .\overrightarrow {AC} }}{{AB.AC}} \)
b) \(AB = \left| {\overrightarrow {AB} } \right| = \sqrt {(x_B - x_A)^2+(y_B-y_A)^2}\)
Lời giải chi tiết:
a) Ta có: \(\overrightarrow {AB} = \left( {60;10} \right),\overrightarrow {AC} = \left( {42; - 43} \right),\overrightarrow {BC} = \left( { - 18; - 53} \right)\)
\(\cos \widehat {BAC} = \cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \frac{{\overrightarrow {AB} .\overrightarrow {AC} }}{{AB.AC}} = \frac{{60.42 + 10.( - 43)}}{{\sqrt {{{60}^2} + {{10}^2}} .\sqrt {{{42}^2} + {{\left( { - 43} \right)}^2}} }} \simeq 0,572 \Rightarrow \widehat {BAC} \approx 55^\circ 8'\)
b)
Khoảng cách từ tàu đến đảo B là \(AB = \left| {\overrightarrow {AB} } \right| = \sqrt {{{60}^2} + {{10}^2}} = 10\sqrt {37} \) (km)
Khoảng cách từ tàu đến đảo B là \(AC = \left| {\overrightarrow {AC} } \right| = \sqrt {{{42}^2} + {{\left( { - 43} \right)}^2}} = \sqrt {3613} \) (km)
Mục 3 trong SGK Toán 10 tập 2 Chân trời sáng tạo là một phần quan trọng, giới thiệu về vectơ và các phép toán cơ bản liên quan. Để giải quyết các bài tập trong mục này, học sinh cần nắm vững định nghĩa vectơ, các phép cộng, trừ, nhân với một số thực, và tích vô hướng của hai vectơ. Ngoài ra, việc hiểu rõ các tính chất của các phép toán này cũng rất quan trọng.
Vectơ là một đoạn thẳng có hướng. Nó được xác định bởi điểm gốc và điểm cuối. Vectơ có độ dài và hướng. Hai vectơ được gọi là bằng nhau nếu chúng có cùng độ dài và cùng hướng. Vectơ không (vectơ 0) là vectơ có điểm gốc và điểm cuối trùng nhau.
Vectơ được sử dụng để biểu diễn các điểm, đường thẳng, và các hình hình học khác. Chúng cũng được sử dụng để chứng minh các tính chất hình học và giải các bài toán liên quan đến khoảng cách, góc, và diện tích.
Dưới đây là giải chi tiết các bài tập trong mục 3 trang 41, 42, 43, 44 SGK Toán 10 tập 2 Chân trời sáng tạo:
(Nội dung bài tập và lời giải chi tiết)
(Nội dung bài tập và lời giải chi tiết)
(Nội dung bài tập và lời giải chi tiết)
(Nội dung bài tập và lời giải chi tiết)
Hy vọng với những kiến thức và lời giải chi tiết trên, các em học sinh đã có thể tự tin giải quyết các bài tập trong mục 3 trang 41, 42, 43, 44 SGK Toán 10 tập 2 Chân trời sáng tạo. Chúc các em học tập tốt và đạt kết quả cao!