Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2 trang 61 và 62 sách giáo khoa Toán 10 tập 2, chương trình Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong quá trình học tập.
Viết phương trình tiếp tuyến của đường tròn (C) tại điểm A(4;6) Một vận động viên ném đĩa đã vung đĩa theo một đường tròn (C) có phương trình:
Viết phương trình tiếp tuyến của đường tròn \((C):{x^2} + {y^2} - 2x - 4y - 20 = 0\) tại điểm \(A(4;6)\).
Phương pháp giải:
Phương trình tiếp tuyến của đường tròn tâm \(I(a;b)\) tại điểm \(M({x_0};{y_0})\)nằm trên đường tròn là: \(\left( {a - {x_0}} \right)\left( {x - {x_0}} \right) + \left( {b - {y_0}} \right)\left( {y - {y_0}} \right) = 0\).
Lời giải chi tiết:
Ta có \({4^2} + {6^2} - 2.4 - 4.6 - 20 = 0\), nên điểm A thuộc (C).
Đường tròn \((C):{x^2} + {y^2} - 2x - 4y - 20 = 0\) có tâm \(I(1;2)\).
Phương trình tiếp tuyến d của (C) tại \(A(4;6)\) là:
\(\left( {1 - 4} \right)\left( {x - 4} \right) + \left( {2 - 6} \right)\left( {y - 6} \right) = 0\)
\(\Leftrightarrow 3x + 4y - 36 = 0\).
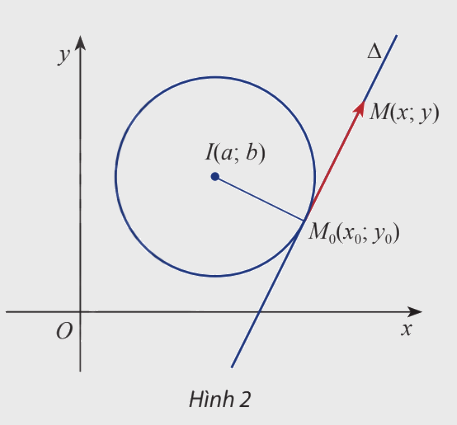
Cho điểm \({M_0}\left( {{x_0};{y_0}} \right)\) nằm trên đường tròn \((C)\) tâm \(I(a;b)\)và cho điểm \(M(x;y)\) tùy ý trong mặt phẳng Oxy. Gọi \(\Delta \) là tiếp tuyến với \((C)\) tại \({M_0}\).
a) Viết biểu thức tọa độ của hai vt \(\overrightarrow {{M_0}M} \) và \(\overrightarrow {{M_0}I} \).
b) Viết biểu thức tọa độ của tích vô hướng của hai vecto \(\overrightarrow {{M_0}M} \) và \(\overrightarrow {{M_0}I} \).
c) Phương trình \(\overrightarrow {{M_0}M} .\overrightarrow {{M_0}I} = 0\) là phương trình của đường thẳng nào?
Phương pháp giải:
a) Với \(A(a;b),B(x;y)\) thì tọa độ của vt \(\overrightarrow {AB} = (x - a;y - b)\).
b) Với \(\overrightarrow a = \left( {a,b} \right),\overrightarrow b = (x;y)\) thì \(\overrightarrow a .\overrightarrow b = ax + by\).
c) Từ tích vô hướng đưa ra kết luận là \(\overrightarrow {{M_0}M} = \left( {x - {x_0};y - {y_0}} \right)\), \(\overrightarrow {{M_0}I} = \left( {a - {x_0};b - {y_0}} \right)\).
Lời giải chi tiết:
a) Biểu thức tọa độ của hai vecto \(\overrightarrow {{M_0}M} \) và \(\overrightarrow {{M_0}I} \) là \(\overrightarrow {{M_0}M} = \left( {x - {x_0};y - {y_0}} \right)\), \(\overrightarrow {{M_0}I} = \left( {a - {x_0};b - {y_0}} \right)\).
b) Ta có:
\(\overrightarrow {{M_0}M} .\overrightarrow {{M_0}I} = \left( {x - {x_0}} \right)\left( {a - {x_0}} \right) + \left( {b - {y_0}} \right)\left( {y - {y_0}} \right)\).
c) \(\overrightarrow {{M_0}M} .\overrightarrow {{M_0}I} = 0 \Rightarrow \overrightarrow {{M_0}M} \bot \overrightarrow {{M_0}I} \)
\({M_0}I\) là đoạn thẳng nối tâm với điểm thuộc đường tròn, suy ra đường thẳng \(M{M_0}\) là tiếp tuyến của đường tròn tại điểm \({M_0}\), hay chính là \(\Delta \).
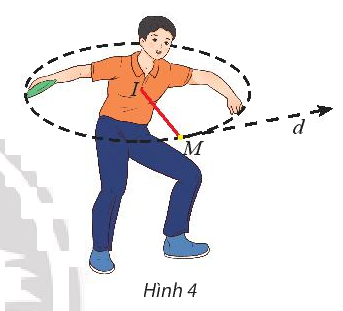
Một vận động viên ném đĩa đã vung đĩa theo một đường tròn \((C)\) có phương trình:
\({\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = \frac{{169}}{{144}}\).
Khi người đó vung đĩa đến vị trí điểm \(M\left( {\frac{{17}}{{12}};2} \right)\) thì buông đĩa (hình 4). Viết phương trình tiếp tuyến của đường tròn \((C)\) tại điểm M.
Phương pháp giải:
Phương trình tiếp tuyến của đường trong tâm \(I(a;b)\) tại điểm \(M({x_0};{y_0})\) nằm trên đường tròn là: \(\left( {a - {x_0}} \right)\left( {x - {x_0}} \right) + \left( {b - {y_0}} \right)\left( {y - {y_0}} \right) = 0\).
Lời giải chi tiết:
Ta có \({\left( {\frac{{17}}{{12}} - 1} \right)^2} + {\left( {2 - 1} \right)^2} = \frac{{169}}{{144}}\), nên điểm M thuộc (C).
Đường tròn \({\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = \frac{{169}}{{144}}\) có tâm \(I(1;1)\).
Phương trình tiếp tuyến d của (C) tại \(M\left( {\frac{{17}}{{12}};2} \right)\) là:
\(\left( {1 - \frac{{17}}{{12}}} \right)\left( {x - \frac{{17}}{{12}}} \right) + \left( {1 - 2} \right)\left( {y - 2} \right) = 0\)
\( \Leftrightarrow - \frac{5}{{12}}x - y + \frac{{373}}{{144}} = 0\)
\( \Leftrightarrow 5x + 12y - \frac{{373}}{{12}} = 0\).
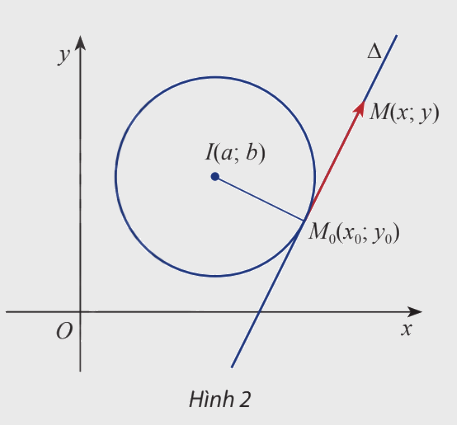
Cho điểm \({M_0}\left( {{x_0};{y_0}} \right)\) nằm trên đường tròn \((C)\) tâm \(I(a;b)\)và cho điểm \(M(x;y)\) tùy ý trong mặt phẳng Oxy. Gọi \(\Delta \) là tiếp tuyến với \((C)\) tại \({M_0}\).
a) Viết biểu thức tọa độ của hai vt \(\overrightarrow {{M_0}M} \) và \(\overrightarrow {{M_0}I} \).
b) Viết biểu thức tọa độ của tích vô hướng của hai vecto \(\overrightarrow {{M_0}M} \) và \(\overrightarrow {{M_0}I} \).
c) Phương trình \(\overrightarrow {{M_0}M} .\overrightarrow {{M_0}I} = 0\) là phương trình của đường thẳng nào?
Phương pháp giải:
a) Với \(A(a;b),B(x;y)\) thì tọa độ của vt \(\overrightarrow {AB} = (x - a;y - b)\).
b) Với \(\overrightarrow a = \left( {a,b} \right),\overrightarrow b = (x;y)\) thì \(\overrightarrow a .\overrightarrow b = ax + by\).
c) Từ tích vô hướng đưa ra kết luận là \(\overrightarrow {{M_0}M} = \left( {x - {x_0};y - {y_0}} \right)\), \(\overrightarrow {{M_0}I} = \left( {a - {x_0};b - {y_0}} \right)\).
Lời giải chi tiết:
a) Biểu thức tọa độ của hai vecto \(\overrightarrow {{M_0}M} \) và \(\overrightarrow {{M_0}I} \) là \(\overrightarrow {{M_0}M} = \left( {x - {x_0};y - {y_0}} \right)\), \(\overrightarrow {{M_0}I} = \left( {a - {x_0};b - {y_0}} \right)\).
b) Ta có:
\(\overrightarrow {{M_0}M} .\overrightarrow {{M_0}I} = \left( {x - {x_0}} \right)\left( {a - {x_0}} \right) + \left( {b - {y_0}} \right)\left( {y - {y_0}} \right)\).
c) \(\overrightarrow {{M_0}M} .\overrightarrow {{M_0}I} = 0 \Rightarrow \overrightarrow {{M_0}M} \bot \overrightarrow {{M_0}I} \)
\({M_0}I\) là đoạn thẳng nối tâm với điểm thuộc đường tròn, suy ra đường thẳng \(M{M_0}\) là tiếp tuyến của đường tròn tại điểm \({M_0}\), hay chính là \(\Delta \).
Viết phương trình tiếp tuyến của đường tròn \((C):{x^2} + {y^2} - 2x - 4y - 20 = 0\) tại điểm \(A(4;6)\).
Phương pháp giải:
Phương trình tiếp tuyến của đường tròn tâm \(I(a;b)\) tại điểm \(M({x_0};{y_0})\)nằm trên đường tròn là: \(\left( {a - {x_0}} \right)\left( {x - {x_0}} \right) + \left( {b - {y_0}} \right)\left( {y - {y_0}} \right) = 0\).
Lời giải chi tiết:
Ta có \({4^2} + {6^2} - 2.4 - 4.6 - 20 = 0\), nên điểm A thuộc (C).
Đường tròn \((C):{x^2} + {y^2} - 2x - 4y - 20 = 0\) có tâm \(I(1;2)\).
Phương trình tiếp tuyến d của (C) tại \(A(4;6)\) là:
\(\left( {1 - 4} \right)\left( {x - 4} \right) + \left( {2 - 6} \right)\left( {y - 6} \right) = 0\)
\(\Leftrightarrow 3x + 4y - 36 = 0\).
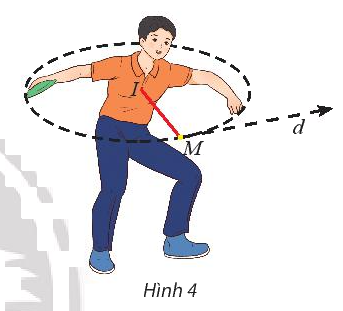
Một vận động viên ném đĩa đã vung đĩa theo một đường tròn \((C)\) có phương trình:
\({\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = \frac{{169}}{{144}}\).
Khi người đó vung đĩa đến vị trí điểm \(M\left( {\frac{{17}}{{12}};2} \right)\) thì buông đĩa (hình 4). Viết phương trình tiếp tuyến của đường tròn \((C)\) tại điểm M.
Phương pháp giải:
Phương trình tiếp tuyến của đường trong tâm \(I(a;b)\) tại điểm \(M({x_0};{y_0})\) nằm trên đường tròn là: \(\left( {a - {x_0}} \right)\left( {x - {x_0}} \right) + \left( {b - {y_0}} \right)\left( {y - {y_0}} \right) = 0\).
Lời giải chi tiết:
Ta có \({\left( {\frac{{17}}{{12}} - 1} \right)^2} + {\left( {2 - 1} \right)^2} = \frac{{169}}{{144}}\), nên điểm M thuộc (C).
Đường tròn \({\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = \frac{{169}}{{144}}\) có tâm \(I(1;1)\).
Phương trình tiếp tuyến d của (C) tại \(M\left( {\frac{{17}}{{12}};2} \right)\) là:
\(\left( {1 - \frac{{17}}{{12}}} \right)\left( {x - \frac{{17}}{{12}}} \right) + \left( {1 - 2} \right)\left( {y - 2} \right) = 0\)
\( \Leftrightarrow - \frac{5}{{12}}x - y + \frac{{373}}{{144}} = 0\)
\( \Leftrightarrow 5x + 12y - \frac{{373}}{{12}} = 0\).
Mục 2 của SGK Toán 10 tập 2 Chân trời sáng tạo tập trung vào việc nghiên cứu về vectơ và các phép toán vectơ cơ bản. Nội dung chính bao gồm định nghĩa vectơ, các loại vectơ đặc biệt (vectơ không, vectơ đối, vectơ đơn vị), phép cộng, trừ vectơ, phép nhân vectơ với một số thực và tính chất của các phép toán này.
Vectơ là một đoạn thẳng có hướng. Một vectơ được xác định bởi điểm gốc và điểm cuối. Vectơ được ký hiệu là AB, trong đó A là điểm gốc và B là điểm cuối. Vectơ không là vectơ có điểm gốc và điểm cuối trùng nhau. Vectơ đối của vectơ AB là vectơ BA. Vectơ đơn vị là vectơ có độ dài bằng 1.
Phép cộng vectơ tuân theo quy tắc hình bình hành. Để cộng hai vectơ a và b, ta vẽ hình bình hành có hai cạnh là a và b. Đường chéo của hình bình hành xuất phát từ điểm gốc của a là vectơ tổng a + b. Phép trừ vectơ a - b được định nghĩa là a + (-b), trong đó -b là vectơ đối của b.
Phép nhân vectơ a với một số thực k (k ≠ 0) được ký hiệu là ka. Vectơ ka có cùng hướng với a nếu k > 0 và ngược hướng với a nếu k < 0. Độ dài của vectơ ka là |k| lần độ dài của vectơ a.
Bài 1: Cho hai vectơ a và b có độ dài lần lượt là 3 và 4, và góc giữa chúng là 60°. Tính độ dài của vectơ a + b.
Lời giải: Sử dụng công thức tính độ dài của vectơ tổng: |a + b|2 = |a|2 + |b|2 + 2|a||b|cos(θ). Thay số vào, ta có: |a + b|2 = 32 + 42 + 2*3*4*cos(60°) = 9 + 16 + 12 = 37. Vậy |a + b| = √37.
Bài 2: Tìm vectơ x sao cho 2x + a = b, với a = (1; 2) và b = (3; 4).
Lời giải: Ta có 2x = b - a = (3 - 1; 4 - 2) = (2; 2). Suy ra x = (1; 1).
Kiến thức về vectơ và các phép toán vectơ có ứng dụng rộng rãi trong nhiều lĩnh vực của toán học và vật lý, như hình học giải tích, cơ học, vật lý học. Việc nắm vững các khái niệm và kỹ năng giải toán liên quan đến vectơ là rất quan trọng để học tốt các môn học khác và giải quyết các bài toán thực tế.
Để củng cố kiến thức và rèn luyện kỹ năng, các em có thể tự giải thêm các bài tập trong SGK và các tài liệu tham khảo khác. Giaitoan.edu.vn sẽ tiếp tục cập nhật thêm nhiều bài giải và hướng dẫn chi tiết để hỗ trợ các em trong quá trình học tập.