Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 16 trang 75 SGK Toán 10 tập 2 – Chân trời sáng tạo. Bài viết này sẽ cung cấp cho bạn các bước giải bài tập một cách dễ hiểu, cùng với những kiến thức nền tảng cần thiết để nắm vững nội dung chương trình học.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, giúp bạn tự tin chinh phục môn Toán.
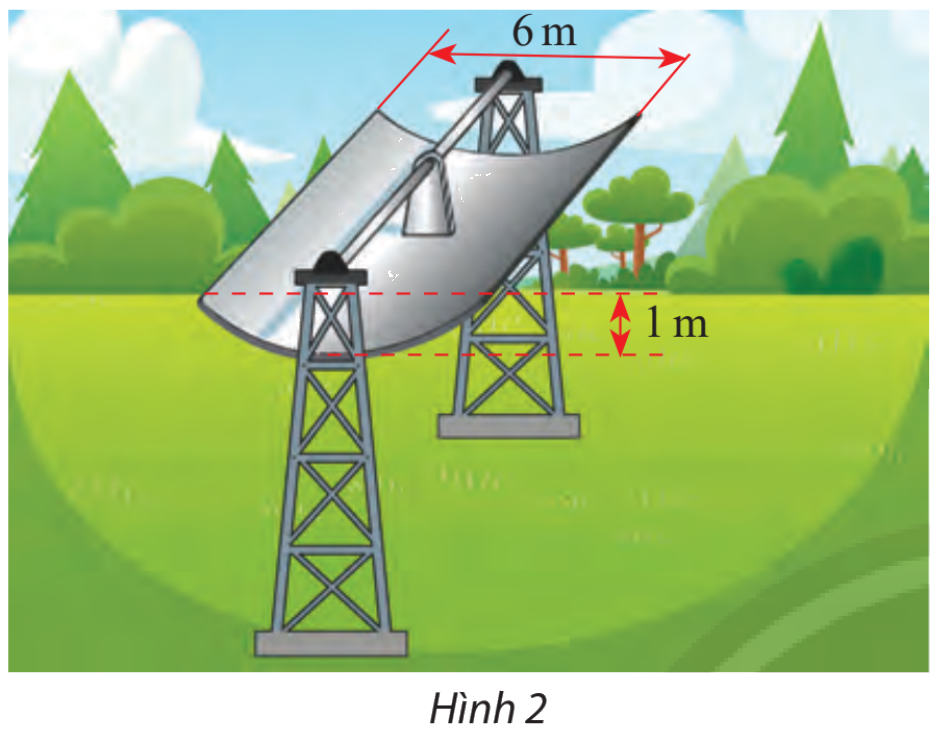
Một bộ thu năng lượng mặt trời để làm nóng nước được làm bằng một tấm thép không gỉ có mặt cắt hình parabol (hình 2). Nước sẽ chảy thông qua một đường ống nằm ở tiêu điểm của parabol
Đề bài
Một bộ thu năng lượng mặt trời để làm nóng nước được làm bằng một tấm thép không gỉ có mặt cắt hình parabol (hình 2). Nước sẽ chảy thông qua một đường ống nằm ở tiêu điểm của parabol
a) Viết phương trình chính tắc của parabol
b) Tính khoảng cách từ tâm đường ống đến đỉnh của parabol
Phương pháp giải - Xem chi tiết
a) Bước 1: Xác định điểm nằm trên đường parabol
Bước 2: Giả sử phương trình của parabol là \({y^2} = 2px\), thay tọa độ điểm vừa tìm được tìm p
Bước 3: Xác định phương trình chính tắc của parabol
b) Xác định tọa độ của tiêu điểm \(F\left( {\frac{p}{2};0} \right)\)
Lời giải chi tiết
a) Vẽ lại parabol mô phỏng mặt cắt trên như hình dưới
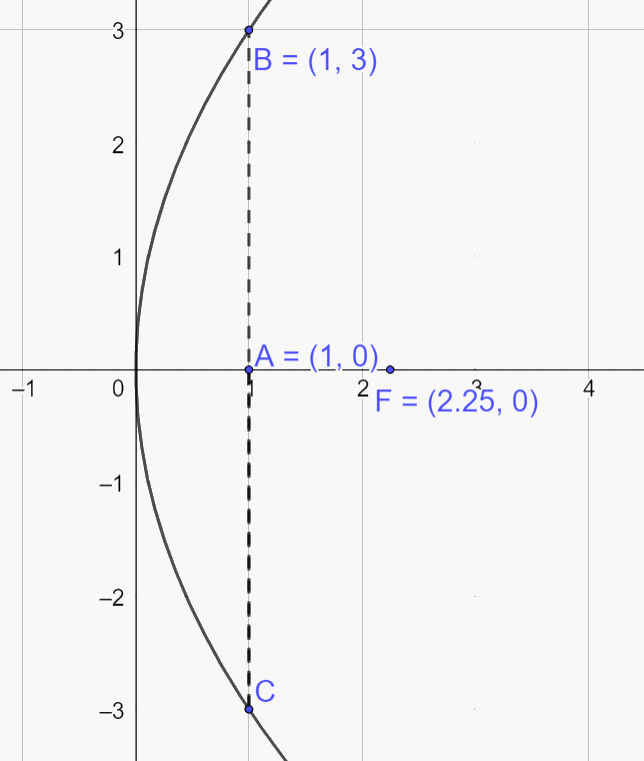
Ta có: \(OA = 1,BC = 2{y_B} = 6 \Rightarrow B\left( {1;3} \right)\)
Giả sử phương trình chính tắc của parabol có dạng \({y^2} = 2px\)
Thay tọa độ điểm B vào phương trình \({y^2} = 2px\) ta có: \({3^2} = 2p.1 \Rightarrow p = \frac{9}{2}\)
Vậy phương trình chính tắc của parabol mô phỏng mặt cắt trên là \({y^2} = 9x\)
b) Khoảng cách từ tâm đường ống đến đỉnh của parabol chính là độ dài từ đỉnh tới tiêu điểm của parabol
Từ phương trình chính tắc ta có tiêu điểm \(F\left( {\frac{9}{4};0} \right)\)
Vậy khoảng cách từ tâm đường ống đến đỉnh của parabol là \(\frac{9}{4}\) m
Bài 16 trang 75 SGK Toán 10 tập 2 – Chân trời sáng tạo thuộc chương trình học về vectơ trong mặt phẳng. Bài tập này yêu cầu học sinh vận dụng kiến thức về tích vô hướng của hai vectơ để giải quyết các bài toán liên quan đến góc giữa hai vectơ, độ dài vectơ và các ứng dụng thực tế.
Bài 16 bao gồm các câu hỏi và bài tập khác nhau, tập trung vào các chủ đề sau:
Để giải bài tập này một cách hiệu quả, bạn cần nắm vững các kiến thức sau:
Dưới đây là lời giải chi tiết cho từng câu hỏi và bài tập trong bài 16:
Áp dụng công thức tính tích vô hướng, ta có:
a.b = (2)(-1) + (3)(4) = -2 + 12 = 10
Ta có a.b = (1)(0) + (0)(1) = 0. Vì tích vô hướng bằng 0, nên hai vectơ a và b vuông góc với nhau. Do đó, góc giữa hai vectơ là 90°.
Theo định nghĩa, hai vectơ a và b vuông góc với nhau khi và chỉ khi góc giữa chúng là 90°. Khi đó, cos(90°) = 0. Áp dụng công thức tích vô hướng, ta có a.b = |a||b|cos(90°) = |a||b|(0) = 0. Vậy, nếu a vuông góc với b thì a.b = 0.
Cho tam giác ABC có A(1; 2), B(3; 4), C(5; 1). Tính độ dài cạnh BC.
Ta có vectơ BC = (5-3; 1-4) = (2; -3). Độ dài cạnh BC là |BC| = √((2)^2 + (-3)^2) = √(4 + 9) = √13.
Bài 16 trang 75 SGK Toán 10 tập 2 – Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về tích vô hướng của hai vectơ và các ứng dụng của nó. Hy vọng rằng với lời giải chi tiết và những lưu ý trên, bạn sẽ tự tin giải quyết bài tập này một cách hiệu quả.