Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10 tập 2 theo chương trình Chân trời sáng tạo. Chúng tôi hiểu rằng việc tự học đôi khi gặp khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy và vận dụng kiến thức.
Mục tiêu của chúng tôi là giúp bạn nắm vững kiến thức Toán học, tự tin giải quyết các bài tập và đạt kết quả tốt nhất trong học tập.
Lợi nhuận (I) thu được trong một ngày làm việc kinh doanh một loại gạo của cửa hàng Các bất phương trình nào sau đây là bất phương trình bậc hai một ẩn? Giải các bất phương trình bậc hai sau: Hãy giải bất phương trình lập được trong hoạt động khám phá và tìm giá bán gạo sao cho cửa hàng có lãi.
Giải các bất phương trình bậc hai sau:
a) \(15{x^2} + 7x - 2 \le 0\)
b) \( - 2{x^2} + x - 3 < 0\)
Phương pháp giải:
Bước 1: Tìm nghiệm của tam thức (nếu có)
Bước 2: Xác định dấu của a
Bước 3: Xét dấu của tam thức
Lời giải chi tiết:
a) Tam thức bậc hai \(f\left( x \right) = 15{x^2} + 7x - 2\) có hai nghiệm phân biệt là \({x_1} = - \frac{2}{3};{x_2} = \frac{1}{5}\)
và có \(a = 15 > 0\) nên \(f\left( x \right) \le 0\) khi x thuộc đoạn \(\left[ { - \frac{2}{3};\frac{1}{5}} \right]\)
Vậy tập nghiệm của bất phương trình \(15{x^2} + 7x - 2 \le 0\) là \(\left[ { - \frac{2}{3};\frac{1}{5}} \right]\)
b) Tam thức bậc hai \(f\left( x \right) = - 2{x^2} + x - 3\) có \(\Delta = - 23 < 0\) và \(a = - 2 < 0\)
nên \(f\left( x \right)\) âm với mọi \(x \in \mathbb{R}\)
Vậy bất phương trình \( - 2{x^2} + x - 3 < 0\) có tập nghiệm là \(\mathbb{R}\)
Các bất phương trình nào sau đây là bất phương trình bậc hai một ẩn? Nếu là bất phương trình bậc hai một ẩn, \(x = 2\)có là nghiệm của bất phương trình đó hay không?
a) \({x^2} + x - 6 \le 0\)
b) \(x + 2 > 0\)
c) \( - 6{x^2} - 7x + 5 > 0\)
Phương pháp giải:
Bước 1: Xác định bậc của bất phương trình và số ẩn, nếu bậc là 2 và có một ẩn thì là bất phương trình bậc hai một ẩn
Bước 2: Thay \(x = 2\)vào bất phương trình, nếu thỏa mãn bất phương trình thì là nghiệm
Lời giải chi tiết:
a) \({x^2} + x - 6 \le 0\) là một bất phương trình bậc hai một ẩn
Vì \({2^2} + 2 - 6 = 0\) nên \(x = 2\) là nghiệm của bất phương trình trên
b) \(x + 2 > 0\) không là bất phương trình bậc hai một ẩn
c) \( - 6{x^2} - 7x + 5 > 0\) là một bất phương trình bậc hai một ẩn
Vì \( - {6.2^2} - 7.2 + 5 = - 33 < 0\) nên \(x = 2\)không là nghiệm của bất phương trình trên
Hãy giải bất phương trình lập được trong hoạt động khám phá và tìm giá bán gạo sao cho cửa hàng có lãi.
Phương pháp giải:
Bước 1: Lập bất phương trình
Bước 2: Tìm nghiệm của tam thức bậc hai (nếu có)
Bước 3: Xác định dấu của tam thức bậc hai một ẩn
Lời giải chi tiết:
Để cửa hàng có lãi thì lợi nhuận lớn hơn 0
Nên ta có bất phương trình như sau: \( - 3{x^2} + 200x - 2325 > 0\)
Tam thức bậc hai \(f\left( x \right) = - 3{x^2} + 200x - 2325\) có hai nghiệm phân biệt là \({x_1} = 15;{x_2} = \frac{{155}}{3}\) và có \(a = - 3 < 0\)
Nên \(f\left( x \right)\) dương khi x nằm trong khoảng \(\left( {15;\frac{{155}}{3}} \right)\)
Vậy bất phương trình \( - 3{x^2} + 200x - 2325 > 0\) có tập nghiệm là \(\left( {15;\frac{{155}}{3}} \right)\)
Với giá trị nào của x thì tam thức bậc hai \(f\left( x \right) = 2{x^2} - 5x + 3\) mang dấu dương?
Phương pháp giải:
Bước 1: Xét dấu của biệt thức \(\Delta = {b^2} - 4ac\)
Bước 2: Tìm nghiệm của tam thức (nếu có), xét dấu của hệ số \(a\)
Bước 3: Lập bảng xét dấu và kết luận.
Lời giải chi tiết:
Tam thức \(f\left( x \right) = 2{x^2} - 5x + 3\) có \(\Delta = 1 > 0\), hai nghiệm phân biệt là \({x_1} = 1,{x_2} = \frac{3}{2}\) và \(a = 2 > 0\)
Ta có bảng xét dấu như sau:
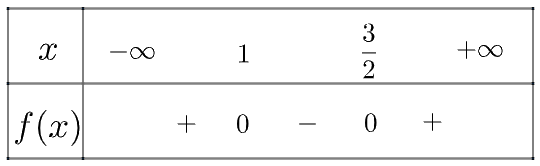
Vậy tam thức đã cho mang dấu dương khi x nằm trong khoảng \(\left( { - \infty ;1} \right) \cup \left( {\frac{3}{2}; + \infty } \right)\)
Lợi nhuận (I) thu được trong một ngày làm việc kinh doanh một loại gạo của cửa hàng phụ thuộc vào giá bán (x) của một kg loại gạo đó theo công thức \(I = - 3{x^2} + 200x - 2325\) với I và x được tính bằng nghìn đồng. Giá trị x như thế nào thì cửa hàng có lãi từ loại gạo đó?

Phương pháp giải:
Bước 1: Xác định của hàng có lãi thì lợi nhuận lớn hơn 0, suy ra \(I > 0\)
Bước 2: Xác định dấu của \(\Delta ,a\) và tìm nghiệm (nếu có)
Bước 3: Lập bảng xét dấu
Lời giải chi tiết:
Để cửa hàng có lãi thì lợi nhuận lớn hơn 0, suy ra \(I > 0 \Leftrightarrow - 3{x^2} + 200x - 2325 > 0\)
Tam thức \(I = - 3{x^2} + 200x - 2325\) có \(\Delta = 12100 > 0\), có hai nghiệm phân biệt \({x_1} = 15;{x_2} = \frac{{155}}{3}\) và có \(a = - 3 < 0\)
Ta có bảng xét dấu như sau:
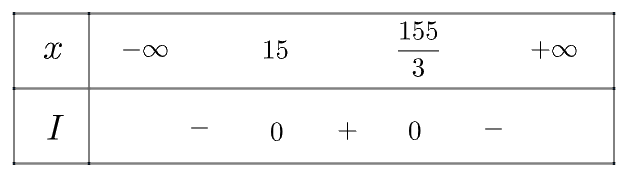
Vậy ta thấy cửa hàng có lợi nhuận khi \(x \in \left( {15;\frac{{155}}{3}} \right)\) (kg)
Với giá trị nào của x thì tam thức bậc hai \(f\left( x \right) = 2{x^2} - 5x + 3\) mang dấu dương?
Phương pháp giải:
Bước 1: Xét dấu của biệt thức \(\Delta = {b^2} - 4ac\)
Bước 2: Tìm nghiệm của tam thức (nếu có), xét dấu của hệ số \(a\)
Bước 3: Lập bảng xét dấu và kết luận.
Lời giải chi tiết:
Tam thức \(f\left( x \right) = 2{x^2} - 5x + 3\) có \(\Delta = 1 > 0\), hai nghiệm phân biệt là \({x_1} = 1,{x_2} = \frac{3}{2}\) và \(a = 2 > 0\)
Ta có bảng xét dấu như sau:
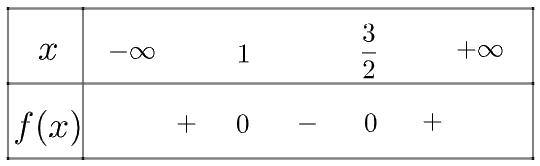
Vậy tam thức đã cho mang dấu dương khi x nằm trong khoảng \(\left( { - \infty ;1} \right) \cup \left( {\frac{3}{2}; + \infty } \right)\)
Lợi nhuận (I) thu được trong một ngày làm việc kinh doanh một loại gạo của cửa hàng phụ thuộc vào giá bán (x) của một kg loại gạo đó theo công thức \(I = - 3{x^2} + 200x - 2325\) với I và x được tính bằng nghìn đồng. Giá trị x như thế nào thì cửa hàng có lãi từ loại gạo đó?

Phương pháp giải:
Bước 1: Xác định của hàng có lãi thì lợi nhuận lớn hơn 0, suy ra \(I > 0\)
Bước 2: Xác định dấu của \(\Delta ,a\) và tìm nghiệm (nếu có)
Bước 3: Lập bảng xét dấu
Lời giải chi tiết:
Để cửa hàng có lãi thì lợi nhuận lớn hơn 0, suy ra \(I > 0 \Leftrightarrow - 3{x^2} + 200x - 2325 > 0\)
Tam thức \(I = - 3{x^2} + 200x - 2325\) có \(\Delta = 12100 > 0\), có hai nghiệm phân biệt \({x_1} = 15;{x_2} = \frac{{155}}{3}\) và có \(a = - 3 < 0\)
Ta có bảng xét dấu như sau:
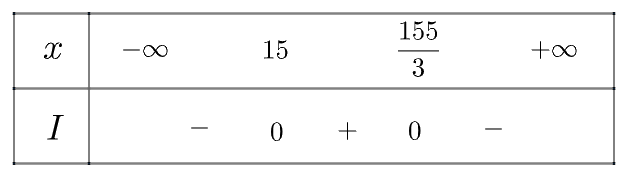
Vậy ta thấy cửa hàng có lợi nhuận khi \(x \in \left( {15;\frac{{155}}{3}} \right)\) (kg)
Các bất phương trình nào sau đây là bất phương trình bậc hai một ẩn? Nếu là bất phương trình bậc hai một ẩn, \(x = 2\)có là nghiệm của bất phương trình đó hay không?
a) \({x^2} + x - 6 \le 0\)
b) \(x + 2 > 0\)
c) \( - 6{x^2} - 7x + 5 > 0\)
Phương pháp giải:
Bước 1: Xác định bậc của bất phương trình và số ẩn, nếu bậc là 2 và có một ẩn thì là bất phương trình bậc hai một ẩn
Bước 2: Thay \(x = 2\)vào bất phương trình, nếu thỏa mãn bất phương trình thì là nghiệm
Lời giải chi tiết:
a) \({x^2} + x - 6 \le 0\) là một bất phương trình bậc hai một ẩn
Vì \({2^2} + 2 - 6 = 0\) nên \(x = 2\) là nghiệm của bất phương trình trên
b) \(x + 2 > 0\) không là bất phương trình bậc hai một ẩn
c) \( - 6{x^2} - 7x + 5 > 0\) là một bất phương trình bậc hai một ẩn
Vì \( - {6.2^2} - 7.2 + 5 = - 33 < 0\) nên \(x = 2\)không là nghiệm của bất phương trình trên
Giải các bất phương trình bậc hai sau:
a) \(15{x^2} + 7x - 2 \le 0\)
b) \( - 2{x^2} + x - 3 < 0\)
Phương pháp giải:
Bước 1: Tìm nghiệm của tam thức (nếu có)
Bước 2: Xác định dấu của a
Bước 3: Xét dấu của tam thức
Lời giải chi tiết:
a) Tam thức bậc hai \(f\left( x \right) = 15{x^2} + 7x - 2\) có hai nghiệm phân biệt là \({x_1} = - \frac{2}{3};{x_2} = \frac{1}{5}\)
và có \(a = 15 > 0\) nên \(f\left( x \right) \le 0\) khi x thuộc đoạn \(\left[ { - \frac{2}{3};\frac{1}{5}} \right]\)
Vậy tập nghiệm của bất phương trình \(15{x^2} + 7x - 2 \le 0\) là \(\left[ { - \frac{2}{3};\frac{1}{5}} \right]\)
b) Tam thức bậc hai \(f\left( x \right) = - 2{x^2} + x - 3\) có \(\Delta = - 23 < 0\) và \(a = - 2 < 0\)
nên \(f\left( x \right)\) âm với mọi \(x \in \mathbb{R}\)
Vậy bất phương trình \( - 2{x^2} + x - 3 < 0\) có tập nghiệm là \(\mathbb{R}\)
Hãy giải bất phương trình lập được trong hoạt động khám phá và tìm giá bán gạo sao cho cửa hàng có lãi.
Phương pháp giải:
Bước 1: Lập bất phương trình
Bước 2: Tìm nghiệm của tam thức bậc hai (nếu có)
Bước 3: Xác định dấu của tam thức bậc hai một ẩn
Lời giải chi tiết:
Để cửa hàng có lãi thì lợi nhuận lớn hơn 0
Nên ta có bất phương trình như sau: \( - 3{x^2} + 200x - 2325 > 0\)
Tam thức bậc hai \(f\left( x \right) = - 3{x^2} + 200x - 2325\) có hai nghiệm phân biệt là \({x_1} = 15;{x_2} = \frac{{155}}{3}\) và có \(a = - 3 < 0\)
Nên \(f\left( x \right)\) dương khi x nằm trong khoảng \(\left( {15;\frac{{155}}{3}} \right)\)
Vậy bất phương trình \( - 3{x^2} + 200x - 2325 > 0\) có tập nghiệm là \(\left( {15;\frac{{155}}{3}} \right)\)
Mục 1 của SGK Toán 10 tập 2 Chân trời sáng tạo thường tập trung vào các khái niệm cơ bản về hàm số bậc hai, bao gồm định nghĩa, các dạng biểu diễn, tính chất và ứng dụng. Việc nắm vững kiến thức này là nền tảng quan trọng để giải quyết các bài tập phức tạp hơn trong chương trình học.
Để giải các bài tập trong Mục 1 trang 11, 12 SGK Toán 10 tập 2 Chân trời sáng tạo, bạn cần nắm vững các kiến thức cơ bản về hàm số bậc hai và áp dụng các phương pháp giải phù hợp. Dưới đây là một số phương pháp thường được sử dụng:
Bài tập: Cho hàm số y = 2x2 - 4x + 1. Hãy tìm trục đối xứng, đỉnh và tập giá trị của hàm số.
Giải:
Khi giải các bài tập về hàm số bậc hai, bạn cần chú ý các điểm sau:
Ngoài SGK Toán 10 tập 2 Chân trời sáng tạo, bạn có thể tham khảo thêm các tài liệu sau để học tập và ôn luyện:
Hy vọng với những kiến thức và phương pháp giải bài tập được trình bày trên đây, bạn sẽ tự tin hơn khi đối mặt với các bài tập trong Mục 1 trang 11, 12 SGK Toán 10 tập 2 Chân trời sáng tạo. Chúc bạn học tập tốt!