Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 15 và 16 sách giáo khoa Toán 10 tập 2, chương trình Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong quá trình học tập.
Lời giải cho phương trình như sau đúng hai sai?
Lời giải cho phương trình \(\sqrt { - 2{x^2} - 2x + 11} = \sqrt { - {x^2} + 3} \) như sau đúng hai sai?
\(\)\(\sqrt { - 2{x^2} - 2x + 11} = \sqrt { - {x^2} + 3} \)
\( \Rightarrow - 2{x^2} - 2x + 11 = - {x^2} + 3\) (bình phương cả hai vế để làm mất dấu căn)
\( \Rightarrow {x^2} + 2x - 8 = 0\) (chuyển vế, rút gọn)
\( \Rightarrow x = 2\) hoặc \(x = - 4\) (giải phương trình bậc hai)
Vậy phương trình đã cho có hai nghiệm là 2 và -4
Lời giải chi tiết:
Thay \(x = 2\) vào phương trình \(\sqrt { - 2{x^2} - 2x + 11} = \sqrt { - {x^2} + 3} \) ta thấy không thỏa mãn vì dưới dấu căn là \( - 1\) không thỏa mãn
Vậy \(x = 2\) không là nghiệm của phương trình do đó lời giải như trên là sai.
Giải phương trình \(\sqrt {31{x^2} - 58x + 1} = \sqrt {10{x^2} - 11x - 19} \)
Phương pháp giải:
Bước 1: Bình phương hai vế của phương trình để làm mất dấu căn
Bước 2: Chuyển vế, rút gọn đưa về phương trình bậc hai một ẩn
Bước 3: Giải phương trình nhận được ở bước 2
Bước 4: Thử lại xem nghiệm đã tìm được ở bước 3 có thỏa mãn phương trình không và kết luận
Lời giải chi tiết:
Bình phương hai vế của phương trình đã cho, ta được:
\(\begin{array}{l}\sqrt {31{x^2} - 58x + 1} = \sqrt {10{x^2} - 11x - 19} \\ \Rightarrow 31{x^2} - 58x + 1 = 10{x^2} - 11x - 19\\ \Rightarrow 21{x^2} - 47x + 20 = 0\end{array}\)
\( \Rightarrow x = \frac{5}{3}\) hoặc \(x = \frac{4}{7}\)
Thay lần lượt các nghiệm trên vào phương trình đã cho, ta thấy không có nghiệm nào thỏa mãn
Vậy phương trình đã cho vô nghiệm
Chú ý khi giải: sau khi bình phương hai vế thì các bước giải tiếp theo chỉ được sử dụng dấu suy ra không được sử dụng dấu tương đương (vì tập nghiệm của chúng có thể không giống nhau)
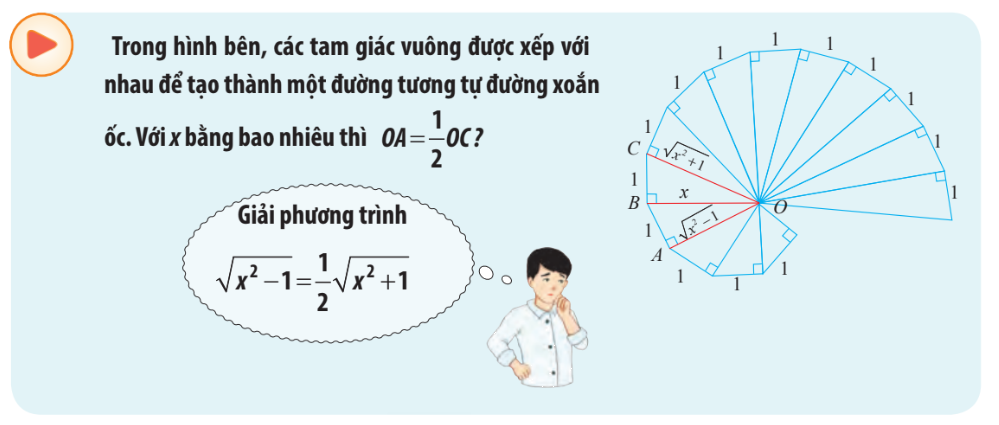
Phương pháp giải:
Bước 1: Bình phương hai vế làm mất căn bậc hai
Bước 2: Rút gọn và giải phương trình vừa tìm được
Bước 3: Thử lại nghiệm vừa tìm được và kết luận
Lời giải chi tiết:
Ta có điều kiện hiểu nhiên \(x > 0\)
\(\begin{array}{l}\sqrt {{x^2} - 1} = \frac{1}{2}\sqrt {{x^2} + 1} \\ \Rightarrow {x^2} - 1 = \frac{1}{4}\left( {{x^2} + 1} \right)\\ \Rightarrow \frac{3}{4}{x^2} - \frac{5}{4} = 0\end{array}\)
\( \Rightarrow x = \pm \sqrt {\frac{5}{3}} \)
Thử lại, kết hợp điều kiện của x ta thấy \(x = \sqrt {\frac{5}{3}} \) thỏa mãn phương trình.
Vậy khi \(x = \sqrt {\frac{5}{3}} \) thì \(OA = \frac{1}{2}OC\)
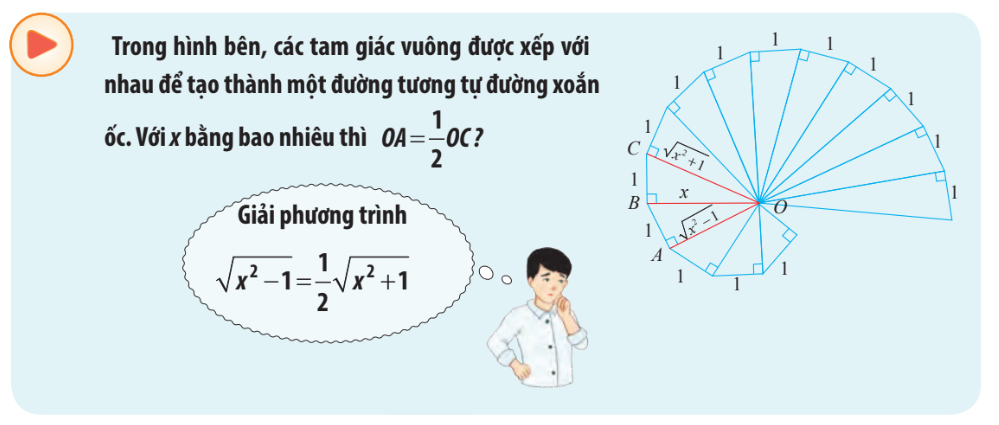
Phương pháp giải:
Bước 1: Bình phương hai vế làm mất căn bậc hai
Bước 2: Rút gọn và giải phương trình vừa tìm được
Bước 3: Thử lại nghiệm vừa tìm được và kết luận
Lời giải chi tiết:
Ta có điều kiện hiểu nhiên \(x > 0\)
\(\begin{array}{l}\sqrt {{x^2} - 1} = \frac{1}{2}\sqrt {{x^2} + 1} \\ \Rightarrow {x^2} - 1 = \frac{1}{4}\left( {{x^2} + 1} \right)\\ \Rightarrow \frac{3}{4}{x^2} - \frac{5}{4} = 0\end{array}\)
\( \Rightarrow x = \pm \sqrt {\frac{5}{3}} \)
Thử lại, kết hợp điều kiện của x ta thấy \(x = \sqrt {\frac{5}{3}} \) thỏa mãn phương trình.
Vậy khi \(x = \sqrt {\frac{5}{3}} \) thì \(OA = \frac{1}{2}OC\)
Lời giải cho phương trình \(\sqrt { - 2{x^2} - 2x + 11} = \sqrt { - {x^2} + 3} \) như sau đúng hai sai?
\(\)\(\sqrt { - 2{x^2} - 2x + 11} = \sqrt { - {x^2} + 3} \)
\( \Rightarrow - 2{x^2} - 2x + 11 = - {x^2} + 3\) (bình phương cả hai vế để làm mất dấu căn)
\( \Rightarrow {x^2} + 2x - 8 = 0\) (chuyển vế, rút gọn)
\( \Rightarrow x = 2\) hoặc \(x = - 4\) (giải phương trình bậc hai)
Vậy phương trình đã cho có hai nghiệm là 2 và -4
Lời giải chi tiết:
Thay \(x = 2\) vào phương trình \(\sqrt { - 2{x^2} - 2x + 11} = \sqrt { - {x^2} + 3} \) ta thấy không thỏa mãn vì dưới dấu căn là \( - 1\) không thỏa mãn
Vậy \(x = 2\) không là nghiệm của phương trình do đó lời giải như trên là sai.
Giải phương trình \(\sqrt {31{x^2} - 58x + 1} = \sqrt {10{x^2} - 11x - 19} \)
Phương pháp giải:
Bước 1: Bình phương hai vế của phương trình để làm mất dấu căn
Bước 2: Chuyển vế, rút gọn đưa về phương trình bậc hai một ẩn
Bước 3: Giải phương trình nhận được ở bước 2
Bước 4: Thử lại xem nghiệm đã tìm được ở bước 3 có thỏa mãn phương trình không và kết luận
Lời giải chi tiết:
Bình phương hai vế của phương trình đã cho, ta được:
\(\begin{array}{l}\sqrt {31{x^2} - 58x + 1} = \sqrt {10{x^2} - 11x - 19} \\ \Rightarrow 31{x^2} - 58x + 1 = 10{x^2} - 11x - 19\\ \Rightarrow 21{x^2} - 47x + 20 = 0\end{array}\)
\( \Rightarrow x = \frac{5}{3}\) hoặc \(x = \frac{4}{7}\)
Thay lần lượt các nghiệm trên vào phương trình đã cho, ta thấy không có nghiệm nào thỏa mãn
Vậy phương trình đã cho vô nghiệm
Chú ý khi giải: sau khi bình phương hai vế thì các bước giải tiếp theo chỉ được sử dụng dấu suy ra không được sử dụng dấu tương đương (vì tập nghiệm của chúng có thể không giống nhau)
Mục 1 của chương trình Toán 10 tập 2, Chân trời sáng tạo tập trung vào việc ôn tập và mở rộng kiến thức về vectơ. Các bài tập trang 15 và 16 SGK Toán 10 tập 2 yêu cầu học sinh vận dụng các khái niệm về vectơ, phép toán vectơ, và ứng dụng của vectơ trong hình học.
Để giúp các em hiểu rõ hơn về cách giải các bài tập trong mục 1, chúng tôi sẽ trình bày lời giải chi tiết cho từng bài tập:
Đề bài: Cho hai vectơ a và b. Tìm vectơ c sao cho a + b = c.
Lời giải: Để tìm vectơ c, ta thực hiện phép cộng vectơ a và b theo quy tắc hình bình hành hoặc quy tắc tam giác. Kết quả của phép cộng vectơ là một vectơ mới có độ dài và hướng xác định.
Đề bài: Cho tam giác ABC. Tìm vectơ AB + BC.
Lời giải: Theo quy tắc cộng vectơ, AB + BC = AC. Do đó, vectơ tổng AB + BC chính là vectơ AC.
Trong mục 1, các bài tập thường gặp bao gồm:
Để giải quyết các bài tập này, các em cần nắm vững các khái niệm cơ bản về vectơ, phép toán vectơ, và quy tắc cộng, trừ vectơ. Ngoài ra, việc vẽ hình minh họa sẽ giúp các em hình dung rõ hơn về bài toán và tìm ra lời giải chính xác.
Để củng cố kiến thức và rèn luyện kỹ năng giải toán, các em có thể tham khảo thêm các tài liệu sau:
Việc luyện tập thường xuyên sẽ giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Khi giải bài tập về vectơ, các em cần lưu ý những điều sau:
Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!