Chào mừng bạn đến với bài học về Lý thuyết Không gian mẫu và biến cố, một phần quan trọng trong chương trình Toán 10 Chân trời sáng tạo. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản nhất về xác suất, giúp bạn hiểu rõ hơn về cách mô tả và phân tích các hiện tượng ngẫu nhiên.
Tại giaitoan.edu.vn, chúng tôi cam kết mang đến cho bạn những bài giảng chất lượng, dễ hiểu và đầy đủ, giúp bạn tự tin chinh phục môn Toán.
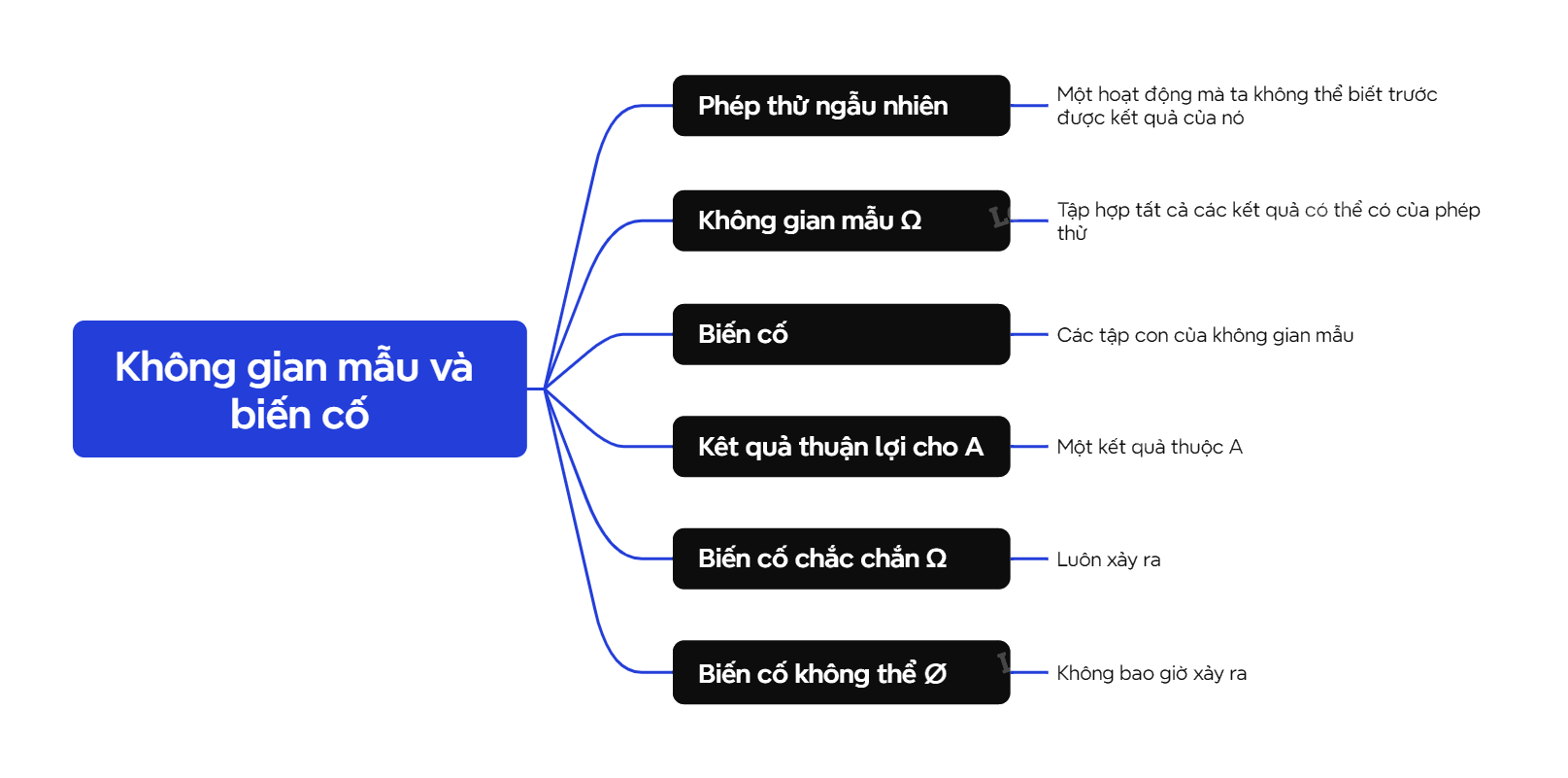
A. Lý thuyết 1. Phép thử ngẫu nhiên và không gian mẫu
A. Lý thuyết
1. Phép thử ngẫu nhiên và không gian mẫu
| Phép thử ngẫu nhiên (gọi tắt là phép thử) là một hoạt động mà ta không thể biết trước được kết quả của nó. Tập hợp tất cả các kết quả có thể có của phép thử ngẫu nhiên được gọi là không gian mẫu, ký hiệu là Ω. |
Chú ý: Trong chương này ta chỉ xét các phép thử mà không gian mẫu gồm hữu hạn phần tử.
2. Biến cố
Mỗi tập con của không gian mẫu được gọi là một biến cố, kí hiệu là A, B, C,… Một kết quả thuộc A được gọi là kết quả làm cho A xảy ra, hoặc kết quả thuận lợi cho A. |
* Biến cố không thể. Biến cố chắc chắn
Biến cố chắc chắn là biến cố luôn xảy ra, kí hiệu là Ω. Biến cố không thể là biến cố không bao giờ xảy ra, kí hiệu là ∅. |
B. Bài tập
Bài 1: Một hộp có 1 quả bóng xanh, 1 quả bóng đỏ, 1 quả bóng vàng; các quả bóng có kích thước và khối lượng giống nhau. Lấy ngẫu nhiên một quả bóng từ trong hộp, ghi lại màu của quả bóng được lấy ra và bỏ lại quả bóng đó vào hộp. Xét phép thử “Lấy ngẫu nhiên tiếp 2 quả bóng trong hộp”. Hãy cho biết không gian mẫu của phép thử đó.
Giải:
Không gian mẫu của phép thử trên là tập hợp Ω = {XX; XD; XV; ĐD; ĐV; DX; DV; VX; VD}, ở đó, chẳng hạn XD là kết quả “Lần thứ nhất lấy ra quả bóng xanh, lần thứ hai lấy ra quả bóng đỏ”.
Bài 2: Một đồng xu có hai mặt, trên một mặt có ghi giá trị của đồng xu, thường gọi là mặt sấp, mặt kia là mặt ngửa. Hãy xác định không gian mẫu cho mỗi phép thử ngẫu nhiên sau:
a) Tung đồng xu một lần.
b) Tung đồng xu hai lần.
Giải:
a) Khi tung đồng xu một lần, ta có không gian mẫu là Ω = {S; N}, trong đó ký hiệu S để chỉ đồng xu xuất hiện mặt sấp.
b) Khi tung đồng xu hai lần, ta có không gian mẫu là Ω = {SS; SN; NS; NN}.
Ở đây ta quy ước SN có nghĩa là lần đầu tung được mặt sấp, lần sau tung được mặt ngửa. Các ký hiệu SS, NS, NN được hiểu một cách tương tự.
Bài 3: Xét phép thử gieo hai con xúc xắc.
a) Hãy xác định không gian mẫu của phép thử.
b) Viết tập hợp mô tả biến cố “Tổng số chấm xuất hiện trên hai con xúc xắc bằng 4”. Có bao nhiêu kết quả thuận lợi cho biến cố đó?
Giải:
a) Kết quả của phép thử là một cặp số (i, j), trong đó i và j lần lượt là số chấm xuất hiện trên con xúc xắc thứ nhất và thứ hai.
Không gian mẫu của phép thử là:
Ω = {(1; 1); (1; 2); (1; 3); (1; 4); (1; 5); (1; 6); (2; 1); (2; 2); (2; 3); (2; 4); (2; 5); (2; 6); (3; 1); (3; 2); (3; 3); (3; 4); (3; 5); (3; 6); (4; 1); (4; 2); (4; 3); (4; 4); (4; 5); (4; 6); (5; 1); (5; 2); (5; 3); (5; 4); (5; 5); (5; 6); (6; 1); (6; 2); (6; 3); (6; 4); (6; 5); (6; 6)}.
Ta cũng có thể viết không gian mẫu dưới dạng: Ω = {(i, j) | i, j = 1, 2, ..., 6}.
b) Gọi A là biến cố “Tổng số chấm xuất hiện bằng 4”. Tập hợp mô tả biến cố A là:
A = {(1; 3); (2; 2); (3; 1)}.
Như vậy, có ba kết quả thuận lợi cho biến cố A.
Bài 4: Một nhóm có 5 bạn nam và 4 bạn nữ. Chọn ngẫu nhiên cùng một lúc ra 3 bạn đi làm công tác tình nguyện.
a) Hãy xác định số phần tử của không gian mẫu.
b) Hãy xác định số các kết quả thuận lợi cho biến cố “Trong 3 bạn được chọn có đúng 2 bạn nữ”.
Giải:
a) Do ta chọn ra 3 bạn khác nhau từ 9 bạn trong nhóm và không tính thứ tự nên số phần tử của không gian mẫu là \(C_9^3 = 84\).
b) Ta có \(C_4^2\) cách chọn ra 2 bạn nữ từ 4 bạn nữ. Ứng với mỗi cách chọn 2 bạn nữ có \(C_5^1\) cách chọn ra 1 bạn nam từ 5 bạn nam.
Theo quy tắc nhân ta có tất cả là \(C_4^2C_5^1\) cách chọn ra 2 bạn nữ và 1 bạn nam từ nhóm bạn.
Do đó số kết quả thuận lợi cho biến có “Trong 3 bạn chọn ra đúng 2 bạn nữ” là: \(C_4^2C_5^1 = 30\).
Trong toán học, đặc biệt là trong lĩnh vực xác suất thống kê, việc hiểu rõ về không gian mẫu và biến cố là vô cùng quan trọng. Đây là nền tảng để xây dựng và giải quyết các bài toán liên quan đến khả năng xảy ra của một sự kiện nào đó.
Định nghĩa: Không gian mẫu là tập hợp tất cả các kết quả có thể xảy ra của một thí nghiệm hoặc một sự kiện ngẫu nhiên.
Ví dụ:
Số phần tử của không gian mẫu được ký hiệu là |Ω| hoặc n(Ω). Số phần tử này đóng vai trò quan trọng trong việc tính toán xác suất.
Định nghĩa: Biến cố là một tập con của không gian mẫu. Nói cách khác, biến cố là một tập hợp các kết quả cụ thể mà chúng ta quan tâm.
Ví dụ:
Biến cố có thể là đơn giản (chỉ chứa một kết quả) hoặc phức tạp (chứa nhiều kết quả).
Bài tập 1: Gieo một con xúc xắc 6 mặt. Xác định không gian mẫu và các biến cố sau:
Giải:
Lý thuyết này có ứng dụng rộng rãi trong nhiều lĩnh vực của đời sống và khoa học, bao gồm:
Để nắm vững kiến thức về Lý thuyết Không gian mẫu và biến cố, bạn nên thực hành giải nhiều bài tập khác nhau. Hãy tìm kiếm các bài tập trong SGK Toán 10 Chân trời sáng tạo và các nguồn tài liệu học tập khác. giaitoan.edu.vn cung cấp đầy đủ các bài tập có đáp án để bạn luyện tập và kiểm tra kiến thức.
Hy vọng bài học này đã giúp bạn hiểu rõ hơn về Lý thuyết Không gian mẫu và biến cố. Chúc bạn học tập tốt!