Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10. Bài viết này sẽ hướng dẫn bạn giải quyết các bài tập trong mục 2 trang 83 sách giáo khoa Toán 10 tập 2, chương trình Chân trời sáng tạo.
Chúng tôi cam kết cung cấp nội dung chính xác, đầy đủ và giúp bạn nắm vững kiến thức Toán học một cách hiệu quả.
Ba bạn Lan, Mai và Đào đặt thẻ học sinh của mình vào một hộp kín, sau đó mỗi bạn lấy ngẫu nhiên một thẻ từ hộp. Tính xác suất của biến cố “Không bạn nào lấy đúng thẻ của mình”
Đề bài
Thực hành 2 trang 83 SGK Toán 10 tập 2 – CTST
Ba bạn Lan, Mai và Đào đặt thẻ học sinh của mình vào một hộp kín, sau đó mỗi bạn lấy ngẫu nhiên một thẻ từ hộp. Tính xác suất của biến cố “Không bạn nào lấy đúng thẻ của mình”
Lời giải chi tiết
Gọi A là biến cố “Không bạn nào lấy đúng thẻ của mình”
Các kết quả có thể xảy ra khi các bạn lần lượt lấy thẻ được thể hiện ở sơ đồ hình cây như hình dưới
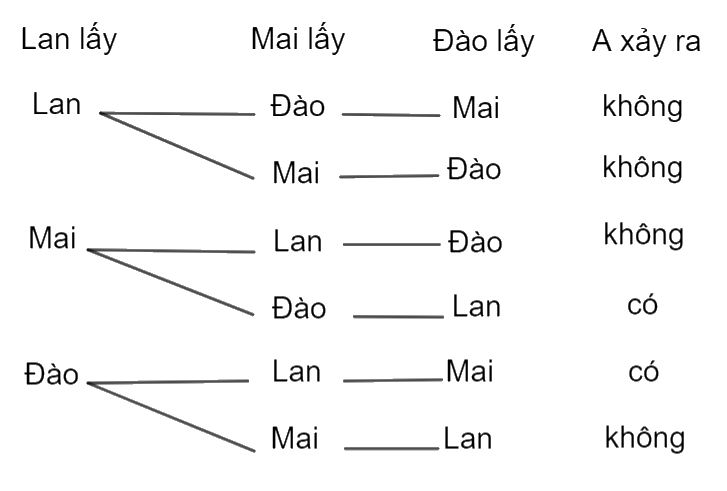
Có tất cả 6 kết quả có thể xảy ra, trong đó có 2 kết quả thuận lợi cho A, do đó:
\(P\left( A \right) = \frac{2}{6} = \frac{1}{3}\)
Mục 2 trang 83 SGK Toán 10 tập 2 - Chân trời sáng tạo thường tập trung vào các ứng dụng thực tế của vectơ trong hình học. Các bài tập thường yêu cầu học sinh vận dụng kiến thức về phép cộng, phép trừ vectơ, tích của một số với vectơ, và các tính chất của vectơ để giải quyết các bài toán liên quan đến hình học phẳng.
Để giúp các em học sinh hiểu rõ hơn về cách giải các bài tập trong mục 2 trang 83, chúng ta sẽ đi vào phân tích chi tiết từng bài tập:
Bài tập này yêu cầu học sinh xác định các vectơ bằng nhau dựa trên độ dài và hướng của chúng. Để giải bài tập này, học sinh cần nắm vững định nghĩa về hai vectơ bằng nhau: hai vectơ được gọi là bằng nhau khi và chỉ khi chúng có cùng độ dài và cùng hướng.
Bài tập này yêu cầu học sinh tìm vectơ đối của một vectơ cho trước. Vectơ đối của một vectơ là vectơ có cùng độ dài nhưng ngược hướng với vectơ ban đầu. Để tìm vectơ đối của một vectơ, học sinh chỉ cần đổi dấu tất cả các thành phần của vectơ ban đầu.
Bài tập này yêu cầu học sinh thực hiện phép cộng và phép trừ vectơ. Để thực hiện phép cộng và phép trừ vectơ, học sinh cần cộng hoặc trừ các thành phần tương ứng của các vectơ. Ví dụ, nếu có hai vectơ a = (x1, y1) và b = (x2, y2), thì a + b = (x1 + x2, y1 + y2) và a - b = (x1 - x2, y1 - y2).
Bài tập này yêu cầu học sinh tính tích của một số với một vectơ. Để tính tích của một số với một vectơ, học sinh cần nhân số đó với mỗi thành phần của vectơ. Ví dụ, nếu có một số k và một vectơ a = (x, y), thì k * a = (k * x, k * y).
Vectơ là một công cụ mạnh mẽ trong việc giải toán hình học. Chúng có thể được sử dụng để biểu diễn các điểm, đường thẳng, và các hình hình học khác. Ngoài ra, vectơ còn có thể được sử dụng để chứng minh các định lý hình học và giải các bài toán liên quan đến diện tích, chu vi, và các tính chất khác của hình học.
Ví dụ: Cho hai điểm A(1, 2) và B(3, 4). Tìm tọa độ của vectơ AB.
Giải: Vectơ AB được tính bằng hiệu tọa độ của điểm B trừ đi tọa độ của điểm A: AB = (3 - 1, 4 - 2) = (2, 2).
Hy vọng rằng với những hướng dẫn chi tiết và ví dụ minh họa trên, các em học sinh đã có thể tự tin giải quyết các bài tập trong mục 2 trang 83 SGK Toán 10 tập 2 - Chân trời sáng tạo. Chúc các em học tập tốt!