Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10 tập 2. Bài viết này sẽ hướng dẫn bạn giải bài 4 trang 17 SGK Toán 10 tập 2 theo chương trình Chân trời sáng tạo.
Chúng tôi cam kết cung cấp nội dung chính xác, đầy đủ và giúp bạn nắm vững kiến thức Toán học một cách hiệu quả.
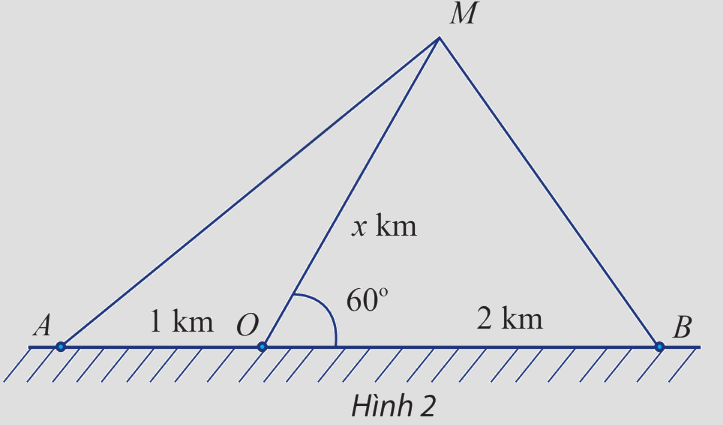
Một con tàu biển M rời cảng O và chuyển động thẳng theo phương tạo với bờ biển một góc 60 độ. Trên bờ biển có hai đài quan sát A và B nằm về hai phía so với cảng O và lần lượt cách cảng O khoảng 1km và 2km (Hình 2).
Đề bài
Một con tàu biển M rời cảng O và chuyển động thẳng theo phương tạo với bờ biển một góc \(60^\circ \). Trên bờ biển có hai đài quan sát A và B nằm về hai phía so với cảng O và lần lượt cách cảng O khoảng 1km và 2km (Hình 2).
a) Đặt độ dài của MO là x km. Biểu diễn khoảng cách từ tàu đến A và từ tàu đến B theo x.
b) Tìm x để khoảng cách từ tàu đến B bằng \(\frac{4}{5}\) khoảng cách từ tàu đến A
c) Tìm x để khoảng cách từ tàu đến B nhỏ hơn khoảng cách từ tàu đến O đúng 500 m.
Lưu ý: Làm tròn kết quả đến hàng phần trăm.
Phương pháp giải - Xem chi tiết
a) Sử dụng định lý cosin \({a^2} = {b^2} + {c^2} + 2bc\cos A\)
b) Lập phương trình \(MB = \frac{4}{5}MA\), và giải phương trình lập được
c) Lập phương trình \(MB = MO - 0,5\), và giải phương trình lập được
Lời giải chi tiết
a) Đặt độ dài của MO là x km \(\left( {x > 0} \right)\)
Ta có: \(\widehat {MOA} + \widehat {MOB} = 180^\circ \) (hai góc bù nhau) \( \Rightarrow \widehat {MOA} = 120^\circ \)
Áp dụng định lý Cosin trong tam giác ta tính được:
+) Khoảng cách từ tàu đến B là \(MB = \sqrt {{x^2} + {2^2} - 2.2.x.\cos 60^\circ } = \sqrt {{x^2} - 2x + 4} \)
+) Khoảng cách từ tàu đến A là \(MA = \sqrt {{x^2} + {1^2} - 2.1.x.\cos 120^\circ } = \sqrt {{x^2} + x + 1} \)
b) Theo giải thiết ta có phương trình \(MB = \frac{4}{5}MA \Rightarrow \sqrt {{x^2} - 2x + 4} = \frac{4}{5}\sqrt {{x^2} + x + 1} \)
\(\begin{array}{l} \Rightarrow {x^2} - 2x + 4 = \frac{{16}}{{25}}\left( {{x^2} + x + 1} \right)\\ \Rightarrow \frac{9}{{25}}{x^2} - \frac{{66}}{{25}}x + \frac{{84}}{{25}} = 0\end{array}\)
\( \Rightarrow x \simeq 1,64\) và \(x \simeq 5,69\)
Thay hai nghiệm vừa tìm được vào phương trình \(\sqrt {{x^2} - 2x + 4} = \frac{4}{5}\sqrt {{x^2} + x + 1} \) ta thấy cả hai nghiệm đều thỏa mãn phương trình
Vậy khi \(x \simeq 1,64\) hoặc \(x \simeq 5,69\) thì khoảng cách từ tàu đến B bằng \(\frac{4}{5}\) khoảng cách từ tàu đến A
c) Đổi 500 m = 0,5 km
Theo giả thiết ta có phương trình sau:
\(\begin{array}{l}MB = MO - 0,5 \Rightarrow \sqrt {{x^2} - 2x + 4} = x - 0,5\\ \Rightarrow {x^2} - 2x + 4 = {\left( {x - 0,5} \right)^2}\\ \Rightarrow {x^2} - 2x + 4 = {x^2} - x + \frac{1}{4}\\ \Rightarrow x = \frac{{15}}{4}\end{array}\)
Thay \(x = \frac{{15}}{4}\) vào phương trình \(\sqrt {{x^2} - 2x + 4} = x - 0,5\) ta thấy thỏa mãn phương trình
Vậy khi \(x = \frac{{15}}{4}\) thì khoảng cách từ tàu đến B nhỏ hơn khoảng cách từ tàu đến O đúng 500 m.
Bài 4 trang 17 SGK Toán 10 tập 2 chương trình Chân trời sáng tạo thuộc chương Hàm số bậc hai. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai, tập xác định, tập giá trị, và các tính chất của hàm số để giải quyết các bài toán cụ thể. Việc nắm vững kiến thức nền tảng và kỹ năng giải bài tập là rất quan trọng để đạt kết quả tốt trong môn Toán.
Bài 4 bao gồm các câu hỏi nhỏ, yêu cầu học sinh:
Tập xác định: Vì hàm số là hàm bậc hai, nên tập xác định là D = ℝ.
Tập giá trị: Hàm số có dạng y = ax2 + bx + c với a = 2 > 0, nên hàm số đạt giá trị nhỏ nhất tại đỉnh của parabol. Hoành độ đỉnh là x = -b/(2a) = 5/4. Giá trị nhỏ nhất là y = 2(5/4)2 - 5(5/4) + 3 = -1/8. Vậy tập giá trị là [ -1/8, +∞ ).
Khoảng đồng biến, nghịch biến: Hàm số nghịch biến trên khoảng (-∞, 5/4) và đồng biến trên khoảng (5/4, +∞).
Tọa độ đỉnh: Đỉnh của parabol là (5/4, -1/8).
Đồ thị: Đồ thị là một parabol có đỉnh (5/4, -1/8) và mở lên trên.
Tập xác định: D = ℝ.
Tập giá trị: Hàm số có dạng y = ax2 + bx + c với a = -1 < 0, nên hàm số đạt giá trị lớn nhất tại đỉnh của parabol. Hoành độ đỉnh là x = -b/(2a) = 2. Giá trị lớn nhất là y = -22 + 4(2) - 1 = 3. Vậy tập giá trị là (-∞, 3].
Khoảng đồng biến, nghịch biến: Hàm số đồng biến trên khoảng (-∞, 2) và nghịch biến trên khoảng (2, +∞).
Tọa độ đỉnh: Đỉnh của parabol là (2, 3).
Đồ thị: Đồ thị là một parabol có đỉnh (2, 3) và mở xuống dưới.
Các bài tập về hàm số bậc hai thường yêu cầu học sinh:
Để giải các bài tập này, bạn cần nắm vững các công thức và tính chất của hàm số bậc hai, đồng thời luyện tập thường xuyên để nâng cao kỹ năng giải toán.
Khi giải bài tập về hàm số bậc hai, bạn cần chú ý:
Bài 4 trang 17 SGK Toán 10 tập 2 – Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc hai. Hy vọng với lời giải chi tiết và các hướng dẫn trên, bạn đã có thể giải bài tập này một cách dễ dàng và hiệu quả. Chúc bạn học tốt!