Chào mừng bạn đến với bài học về Lý thuyết Mệnh đề trong chương trình Toán 10 Chân trời sáng tạo tại giaitoan.edu.vn. Đây là một phần kiến thức quan trọng, đặt nền móng cho các khái niệm toán học phức tạp hơn trong tương lai.
Chúng tôi cung cấp lý thuyết đầy đủ, dễ hiểu cùng với các bài tập minh họa có đáp án chi tiết, giúp bạn tự tin chinh phục môn Toán.
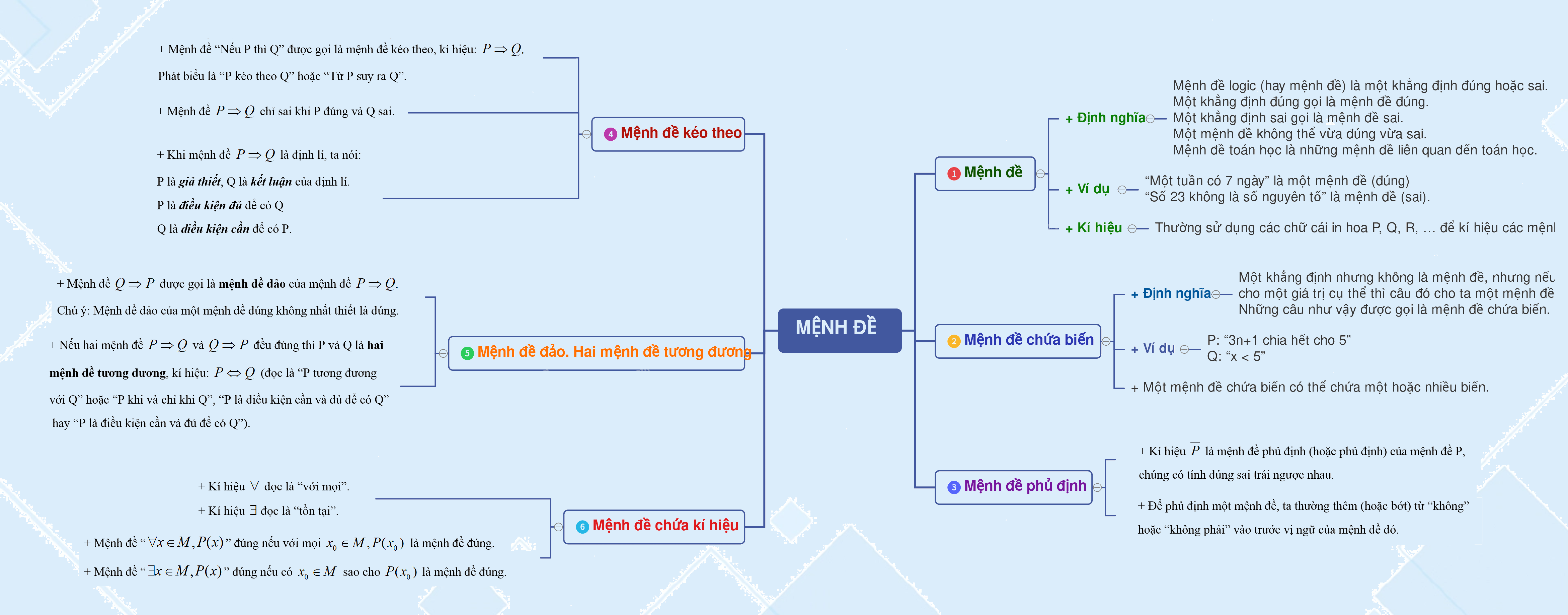
1. Mệnh đề 2. Mệnh đề chứa biến 3. Mệnh đề phủ định
1. Mệnh đề
+ Định nghĩa:
Mệnh đề logic (hay mệnh đề) là một khẳng định đúng hoặc sai.
Một khẳng định đúng gọi là mệnh đề đúng.
Một khẳng định sai gọi là mệnh đề sai.
Một mệnh đề không thể vừa đúng vừa sai.
Mệnh đề toán học là những mệnh đề liên quan đến toán học.
+ Ví dụ:
“Một tuần có 7 ngày” là một mệnh đề (đúng)
“Số 23 không là số nguyên tố” là mệnh đề (sai).
+ Kí hiệu: Thường sử dụng các chữ cái in hoa P, Q, R, … để kí hiệu các mệnh đề.
2. Mệnh đề chứa biến
+ Một khẳng định nhưng không là mệnh đề, nhưng nếu cho một giá trị cụ thể thì câu đó cho ta một mệnh đề. Những câu như vậy được gọi là mệnh đề chứa biến.
Ví dụ: P: “3n+1 chia hết cho 5”
Q: “x < 5”
+ Một mệnh đề chứa biến có thể chứa một hoặc nhiều biến.
3. Mệnh đề phủ định
+ Kí hiệu \(\overline P \) là mệnh đề phủ định (hoặc phủ định) của mệnh đề P, chúng có tính đúng sai trái ngược nhau.
+ Để phủ định một mệnh đề, ta thường thêm (hoặc bớt) từ “không” hoặc “không phải” vào trước vị ngữ của mệnh đề đó.
4. Mệnh đề kéo theo
+ Mệnh đề “Nếu P thì Q” được gọi là mệnh đề kéo theo, kí hiệu: \(P \Rightarrow Q.\) Phát biểu là “P kéo theo Q” hoặc “Từ P suy ra Q”.
+ Mệnh đề \(P \Rightarrow Q\) chỉ sai khi P đúng và Q sai.
+ Khi mệnh đề \(P \Rightarrow Q\) là định lí, ta nói:
P là giả thiết, Q là kết luận của định lí.
P là điều kiện đủ để có Q
Q là điều kiện cần để có P.
5. Mệnh đề đảo. Hai mệnh đề tương đương
+ Mệnh đề \(Q \Rightarrow P\) được gọi là mệnh đề đảo của mệnh đề \(P \Rightarrow Q.\)
Chú ý: Mệnh đề đảo của một mệnh đề đúng không nhất thiết là đúng.
+ Nếu hai mệnh đề \(P \Rightarrow Q\) và \(Q \Rightarrow P\) đều đúng thì P và Q là hai mệnh đề tương đương, kí hiệu: \(P \Leftrightarrow Q\) (đọc là “P tương đương với Q” hoặc “P khi và chỉ khi Q”, “P là điều kiện cần và đủ để có Q” hay “P là điều kiện cần và đủ để có Q”).
6. Mệnh đề chứa kí hiệu \(\forall ,\exists \)
+ Kí hiệu \(\forall \) đọc là “với mọi”.
+ Kí hiệu \(\exists \) đọc là “tồn tại”.
Ví dụ:
“Mọi số thực đều có bình phương lớn hơn 2” viết là: “\(\forall x \in \mathbb{R}|{x^2} > 2\)”
“Có một số thực có bình phương nhỏ hơn 2” viết là: “\(\exists \;x \in \mathbb{R}|{x^2} < 2\)”
+ Mệnh đề “\(\forall x \in M,P(x)\)” đúng nếu với mọi \({x_0} \in M,P({x_0})\) là mệnh đề đúng.
+ Mệnh đề “\(\exists x \in M,P(x)\)” đúng nếu có \({x_0} \in M\) sao cho \(P({x_0})\) là mệnh đề đúng.
Mệnh đề là một câu khẳng định có thể đúng hoặc sai, nhưng không đồng thời cả hai. Trong chương trình Toán 10 Chân trời sáng tạo, việc nắm vững lý thuyết mệnh đề là vô cùng quan trọng, bởi nó là nền tảng cho việc học tập các khái niệm logic và chứng minh toán học.
Một mệnh đề thường được biểu diễn bằng một câu trần thuật đơn giản. Ví dụ:
Lưu ý rằng, câu hỏi, câu cảm thán, câu mệnh lệnh không phải là mệnh đề.
Có hai loại mệnh đề chính:
Phủ định của một mệnh đề P, ký hiệu là ¬P, là một mệnh đề có giá trị chân lý ngược lại với P. Nếu P đúng thì ¬P sai, và ngược lại.
Ví dụ:
Mệnh đề kéo theo có dạng "Nếu P thì Q", ký hiệu là P ⇒ Q. P được gọi là giả thiết, Q được gọi là kết luận.
Bảng chân trị của mệnh đề kéo theo:
| P | Q | P ⇒ Q |
|---|---|---|
| Đúng | Đúng | Đúng |
| Đúng | Sai | Sai |
| Sai | Đúng | Đúng |
| Sai | Sai | Đúng |
Mệnh đề tương đương có dạng "P tương đương Q", ký hiệu là P ⇔ Q. P ⇔ Q tương đương với (P ⇒ Q) và (Q ⇒ P).
Bảng chân trị của mệnh đề tương đương:
| P | Q | P ⇔ Q |
|---|---|---|
| Đúng | Đúng | Đúng |
| Đúng | Sai | Sai |
| Sai | Đúng | Sai |
| Sai | Sai | Đúng |
Lượng từ được sử dụng để biểu thị số lượng các phần tử thỏa mãn một tính chất nào đó.
Bài 1: Xác định xem mệnh đề sau đúng hay sai: "5 là số nguyên tố."
Giải: Mệnh đề này đúng.
Bài 2: Tìm phủ định của mệnh đề: "Mọi học sinh đều chăm học."
Giải: Phủ định của mệnh đề là: "Tồn tại một học sinh không chăm học."
Lý thuyết Mệnh đề là một phần quan trọng trong chương trình Toán 10 Chân trời sáng tạo. Việc hiểu rõ các khái niệm và vận dụng linh hoạt các quy tắc logic sẽ giúp bạn giải quyết các bài toán một cách hiệu quả. Hãy luyện tập thường xuyên để nắm vững kiến thức này nhé!