Chào mừng các em học sinh đến với lời giải chi tiết bài 4 trang 101 SGK Toán 10 tập 1 – Chân trời sáng tạo. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập một cách dễ hiểu và hiệu quả.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán, giúp các em nắm vững kiến thức và đạt kết quả tốt nhất.
Cho đoạn thẳng AB có O là trung điểm và cho điểm M tùy ý. Chứng minh rằng:
Đề bài
Cho đoạn thẳng AB có O là trung điểm và cho điểm M tùy ý. Chứng minh rằng:
\(\overrightarrow {MA} .\overrightarrow {MB} = {\overrightarrow {MO} ^2} - {\overrightarrow {OA} ^2}\)
Phương pháp giải - Xem chi tiết
Sử dụng hằng đẳng thức \({a^2} - {b^2} = \left( {a - b} \right)\left( {a + b} \right)\) phân tích \({\overrightarrow {MO} ^2} - {\overrightarrow {OA} ^2}\)
Lời giải chi tiết
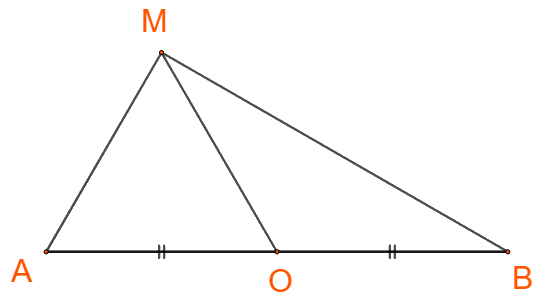
Ta có: \(\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow 0 \Leftrightarrow - \overrightarrow {OA} = \overrightarrow {OB} \)
\(\Rightarrow {\overrightarrow {MO} ^2} - {\overrightarrow {OA} ^2} = \left( {\overrightarrow {MO} + \overrightarrow {OA} } \right)\left( {\overrightarrow {MO} - \overrightarrow {OA} } \right) \\= \left( {\overrightarrow {MO} + \overrightarrow {OA} } \right)\left( {\overrightarrow {MO} + \overrightarrow {OB} } \right) = \overrightarrow {MA} .\overrightarrow {MB} \) (đpcm)
Bài 4 trang 101 SGK Toán 10 tập 1 – Chân trời sáng tạo thuộc chương trình học Toán 10, tập trung vào việc vận dụng các kiến thức về vectơ trong mặt phẳng để giải quyết các bài toán hình học. Bài tập này yêu cầu học sinh hiểu rõ các khái niệm như vectơ, phép cộng, phép trừ vectơ, tích của một số với vectơ, và các tính chất liên quan.
Bài 4 thường bao gồm các dạng bài tập sau:
Để giải quyết bài 4 trang 101 SGK Toán 10 tập 1 – Chân trời sáng tạo một cách hiệu quả, học sinh cần:
Ví dụ: Cho hai vectơ a = (2; -1) và b = (-1; 3). Tính a + b và 2a.
Giải:
a + b = (2 + (-1); -1 + 3) = (1; 2)
2a = (2 * 2; 2 * (-1)) = (4; -2)
Để củng cố kiến thức và kỹ năng giải bài tập về vectơ, học sinh nên luyện tập thêm các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Việc luyện tập thường xuyên sẽ giúp học sinh nắm vững kiến thức và tự tin hơn khi giải các bài tập khó.
Trong quá trình học tập, nếu gặp khó khăn, học sinh nên tìm sự giúp đỡ của giáo viên, bạn bè hoặc tham khảo các nguồn tài liệu trực tuyến. Đừng ngại đặt câu hỏi và trao đổi kiến thức với những người xung quanh. Chúc các em học tập tốt!
| Công thức | Mô tả |
|---|---|
| a + b = (xa + xb; ya + yb) | Phép cộng vectơ |
| a - b = (xa - xb; ya - yb) | Phép trừ vectơ |
| k * a = (k * xa; k * ya) | Tích của một số với vectơ |