Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 2 trang 90, 91 SGK Toán 10 tập 1 chương trình Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập một cách khoa học, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Bài tập mục 2 tập trung vào các kiến thức về vectơ, phép toán vectơ và ứng dụng của vectơ trong hình học.
Cho 3 vectơ a, b, c được biểu diễn như hình 9. Hãy hoàn thành các phép cộng vectơ sau và so sánh kết quả tìm được: Cho hình vuông ABCD có cạnh bằng 1. Tính độ dài các vectơ sau:
Cho hình vuông ABCD có cạnh bằng 1. Tính độ dài các vectơ sau:
a) \(\overrightarrow a = \left( {\overrightarrow {AC} + \overrightarrow {BD} } \right) + \overrightarrow {CB} ;\)
b) \(\overrightarrow a = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {BC} + \overrightarrow {DA} .\)
Phương pháp giải:
Bước 1: Sử dụng tính chất giao hoán, kết hợp, cộng với vectơ \(\overrightarrow 0 \) tìm tổng các vectơ
Bước 2: Tính độ dài vectơ vừa tìm đc, độ dài vectơ \(\overrightarrow {AB} \) là \(\left|
Lời giải chi tiết:
a) \(\begin{array}{l}\overrightarrow a = \left( {\overrightarrow {AC} + \overrightarrow {BD} } \right) + \overrightarrow {CB} = \left( {\overrightarrow {AC} + \overrightarrow {CB} } \right) + \overrightarrow {BD} \\ = \overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {AD}\\ \Rightarrow |{\overrightarrow a}|= \left| {\overrightarrow {AD} } \right| = AD = 1\end{array}\)
b) \(\begin{array}{l}\overrightarrow a = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {BC} + \overrightarrow {DA} = \left( {\overrightarrow {AB} + \overrightarrow {BC} } \right) + \left( {\overrightarrow {AD} + \overrightarrow {DA} } \right)\\ = \overrightarrow {AC} + \overrightarrow {AA} = \overrightarrow {AC} + \overrightarrow 0 = \overrightarrow {AC} \end{array}\)
\(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{1^2} + {1^2}} = \sqrt 2 \)
\(\Rightarrow |{\overrightarrow a}|= \left| {\overrightarrow {AC} } \right| = \sqrt 2 \)
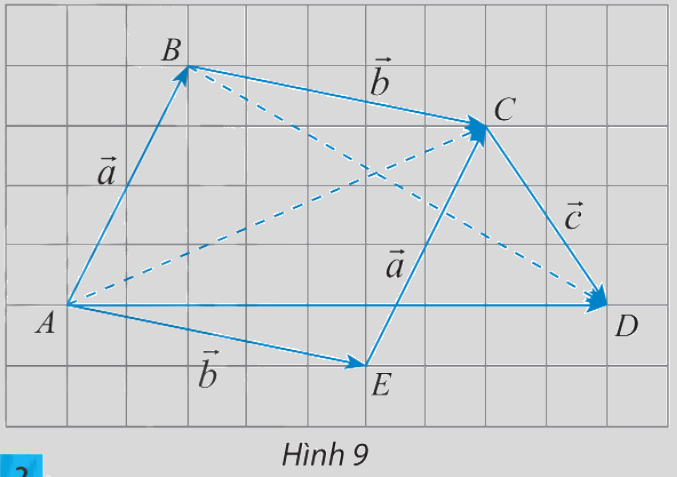
Cho 3 vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) được biểu diễn như hình 9. Hãy hoàn thành các phép cộng vectơ sau và so sánh kết quả tìm được:
a) \(\overrightarrow a + \overrightarrow b = \overrightarrow {AB} + \overrightarrow {BC} = ?\)
\(\overrightarrow b + \overrightarrow a = \overrightarrow {AE} + \overrightarrow {EC} = ?\)
b) \(\left( {\overrightarrow a + \overrightarrow b } \right) + \overrightarrow c = \left( {\overrightarrow {AB} + \overrightarrow {BC} } \right) + \overrightarrow {CD} = \overrightarrow {AC} + \overrightarrow {CD} = ?\)
\(\overrightarrow a + \left( {\overrightarrow b + \overrightarrow c } \right) = \overrightarrow {AB} + \left( {\overrightarrow {BC} + \overrightarrow {CD} } \right) = \overrightarrow {AB} + \overrightarrow {BD} = ?\)
Phương pháp giải:
Bước 1: Áp dụng quy tắc 3 điểm: \( \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \);
Bước 2: So sánh các vectơ vừa tìm được
Lời giải chi tiết:
a) Áp dụng quy tắc ba điểm ta có:
\(\overrightarrow a + \overrightarrow b = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \);
\(\overrightarrow b + \overrightarrow a = \overrightarrow {AE} + \overrightarrow {EC} = \overrightarrow {AC} \)
\( \Rightarrow \overrightarrow a + \overrightarrow b = \overrightarrow b + \overrightarrow a \)
b) Áp dụng quy tắc ba điểm ta có:
\(\left( {\overrightarrow a + \overrightarrow b } \right) + \overrightarrow c = \left( {\overrightarrow {AB} + \overrightarrow {BC} } \right) + \overrightarrow {CD} = \overrightarrow {AC} + \overrightarrow {CD} = \overrightarrow {AD} \)
\(\overrightarrow a + \left( {\overrightarrow b + \overrightarrow c } \right) = \overrightarrow {AB} + \left( {\overrightarrow {BC} + \overrightarrow {CD} } \right) = \overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {AD} \)
\( \Rightarrow \left( {\overrightarrow a + \overrightarrow b } \right) + \overrightarrow c = \overrightarrow a + \left( {\overrightarrow b + \overrightarrow c } \right)\)
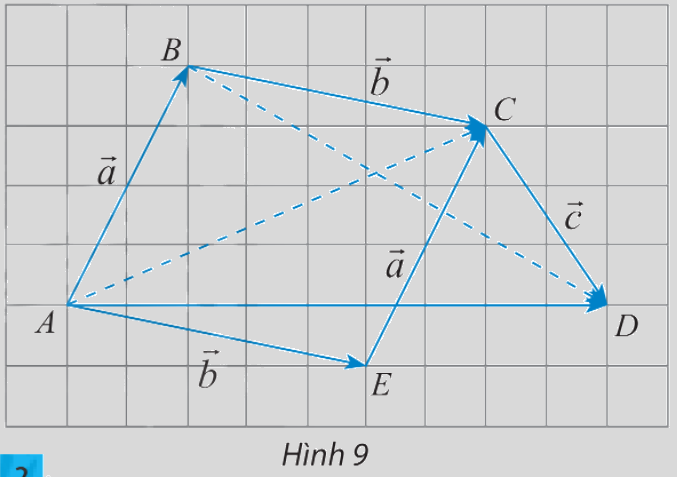
Cho 3 vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) được biểu diễn như hình 9. Hãy hoàn thành các phép cộng vectơ sau và so sánh kết quả tìm được:
a) \(\overrightarrow a + \overrightarrow b = \overrightarrow {AB} + \overrightarrow {BC} = ?\)
\(\overrightarrow b + \overrightarrow a = \overrightarrow {AE} + \overrightarrow {EC} = ?\)
b) \(\left( {\overrightarrow a + \overrightarrow b } \right) + \overrightarrow c = \left( {\overrightarrow {AB} + \overrightarrow {BC} } \right) + \overrightarrow {CD} = \overrightarrow {AC} + \overrightarrow {CD} = ?\)
\(\overrightarrow a + \left( {\overrightarrow b + \overrightarrow c } \right) = \overrightarrow {AB} + \left( {\overrightarrow {BC} + \overrightarrow {CD} } \right) = \overrightarrow {AB} + \overrightarrow {BD} = ?\)
Phương pháp giải:
Bước 1: Áp dụng quy tắc 3 điểm: \( \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \);
Bước 2: So sánh các vectơ vừa tìm được
Lời giải chi tiết:
a) Áp dụng quy tắc ba điểm ta có:
\(\overrightarrow a + \overrightarrow b = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \);
\(\overrightarrow b + \overrightarrow a = \overrightarrow {AE} + \overrightarrow {EC} = \overrightarrow {AC} \)
\( \Rightarrow \overrightarrow a + \overrightarrow b = \overrightarrow b + \overrightarrow a \)
b) Áp dụng quy tắc ba điểm ta có:
\(\left( {\overrightarrow a + \overrightarrow b } \right) + \overrightarrow c = \left( {\overrightarrow {AB} + \overrightarrow {BC} } \right) + \overrightarrow {CD} = \overrightarrow {AC} + \overrightarrow {CD} = \overrightarrow {AD} \)
\(\overrightarrow a + \left( {\overrightarrow b + \overrightarrow c } \right) = \overrightarrow {AB} + \left( {\overrightarrow {BC} + \overrightarrow {CD} } \right) = \overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {AD} \)
\( \Rightarrow \left( {\overrightarrow a + \overrightarrow b } \right) + \overrightarrow c = \overrightarrow a + \left( {\overrightarrow b + \overrightarrow c } \right)\)
Cho hình vuông ABCD có cạnh bằng 1. Tính độ dài các vectơ sau:
a) \(\overrightarrow a = \left( {\overrightarrow {AC} + \overrightarrow {BD} } \right) + \overrightarrow {CB} ;\)
b) \(\overrightarrow a = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {BC} + \overrightarrow {DA} .\)
Phương pháp giải:
Bước 1: Sử dụng tính chất giao hoán, kết hợp, cộng với vectơ \(\overrightarrow 0 \) tìm tổng các vectơ
Bước 2: Tính độ dài vectơ vừa tìm đc, độ dài vectơ \(\overrightarrow {AB} \) là \(\left|
Lời giải chi tiết:
a) \(\begin{array}{l}\overrightarrow a = \left( {\overrightarrow {AC} + \overrightarrow {BD} } \right) + \overrightarrow {CB} = \left( {\overrightarrow {AC} + \overrightarrow {CB} } \right) + \overrightarrow {BD} \\ = \overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {AD}\\ \Rightarrow |{\overrightarrow a}|= \left| {\overrightarrow {AD} } \right| = AD = 1\end{array}\)
b) \(\begin{array}{l}\overrightarrow a = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {BC} + \overrightarrow {DA} = \left( {\overrightarrow {AB} + \overrightarrow {BC} } \right) + \left( {\overrightarrow {AD} + \overrightarrow {DA} } \right)\\ = \overrightarrow {AC} + \overrightarrow {AA} = \overrightarrow {AC} + \overrightarrow 0 = \overrightarrow {AC} \end{array}\)
\(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{1^2} + {1^2}} = \sqrt 2 \)
\(\Rightarrow |{\overrightarrow a}|= \left| {\overrightarrow {AC} } \right| = \sqrt 2 \)
Mục 2 của SGK Toán 10 tập 1 chương trình Chân trời sáng tạo tập trung vào việc củng cố kiến thức về vectơ, bao gồm các khái niệm cơ bản, các phép toán trên vectơ (cộng, trừ, nhân với một số thực) và ứng dụng của vectơ trong việc giải quyết các bài toán hình học.
Bài tập này yêu cầu học sinh xác định vectơ chỉ phương của một đường thẳng cho trước. Để giải bài tập này, học sinh cần nắm vững khái niệm vectơ chỉ phương và cách tìm vectơ chỉ phương từ phương trình đường thẳng hoặc từ hai điểm thuộc đường thẳng.
Ví dụ: Cho đường thẳng d có phương trình 2x + y - 3 = 0. Tìm vectơ chỉ phương của đường thẳng d.
Lời giải: Đường thẳng d có dạng tổng quát Ax + By + C = 0. Vectơ pháp tuyến của đường thẳng d là n = (A, B) = (2, 1). Vectơ chỉ phương của đường thẳng d là u = (-B, A) = (-1, 2).
Bài tập này yêu cầu học sinh kiểm tra xem ba điểm cho trước có thẳng hàng hay không. Để giải bài tập này, học sinh có thể sử dụng phương pháp kiểm tra xem hai vectơ tạo bởi ba điểm có cùng phương hay không.
Ví dụ: Cho ba điểm A(1; 2), B(3; 4), C(5; 6). Chứng minh rằng ba điểm A, B, C thẳng hàng.
Lời giải: Vectơ AB = (3 - 1, 4 - 2) = (2, 2). Vectơ AC = (5 - 1, 6 - 2) = (4, 4). Ta thấy AC = 2AB, do đó hai vectơ AB và AC cùng phương. Vậy ba điểm A, B, C thẳng hàng.
Bài tập này yêu cầu học sinh tìm tọa độ của một điểm thỏa mãn một điều kiện cho trước liên quan đến vectơ. Để giải bài tập này, học sinh cần sử dụng các công thức về tọa độ vectơ và các phép toán trên vectơ.
Ví dụ: Cho A(2; -1), B(4; 3). Tìm tọa độ điểm M sao cho MA = MB.
Lời giải: Gọi M(x; y). Ta có MA = (2 - x, -1 - y) và MB = (4 - x, 3 - y). Vì MA = MB nên ta có hệ phương trình:
Giải hệ phương trình này, ta thấy không có nghiệm. Điều này có nghĩa là không có điểm M nào thỏa mãn điều kiện MA = MB.
Hy vọng với lời giải chi tiết và phương pháp giải bài tập trên, các em học sinh sẽ tự tin hơn trong việc học tập môn Toán 10. Chúc các em học tốt!