Chào mừng các em học sinh đến với lời giải chi tiết bài 6 trang 78 SGK Toán 10 tập 1 – Chân trời sáng tạo. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập một cách dễ hiểu và hiệu quả.
Giaitoan.edu.vn là địa chỉ học toán online uy tín, cung cấp đầy đủ các bài giải SGK Toán 10, bài tập trắc nghiệm và các tài liệu học tập hữu ích khác.
Một người đứng ở trên một tháp truyền hình cao 352 m so với mặt đất, muốn xác định khoảng cách giữa hai cột mốc trên mặt dất bên dưới. Người đó quan sát thấy góc được tạo bởi hai đường ngắm tới hai mốc này là
Đề bài
Một người đứng ở trên một tháp truyền hình cao 352 m so với mặt đất, muốn xác định khoảng cách giữa hai cột mốc trên mặt dất bên dưới. Người đó quan sát thấy góc được tạo bởi hai đường ngắm tới hai mốc này là \({43^ \circ }\), góc giữa phương thẳng đứng và đường ngắm tới một điểm mốc trên mặt đất là \({62^ \circ }\) và đến điểm mốc khác là \({54^ \circ }\)(Hình 11). Tính khoảng cách giữa hai cột mốc này.
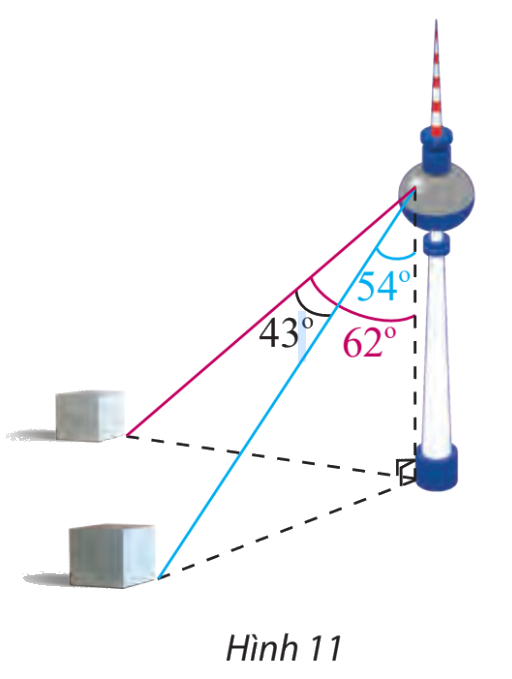
Phương pháp giải - Xem chi tiết
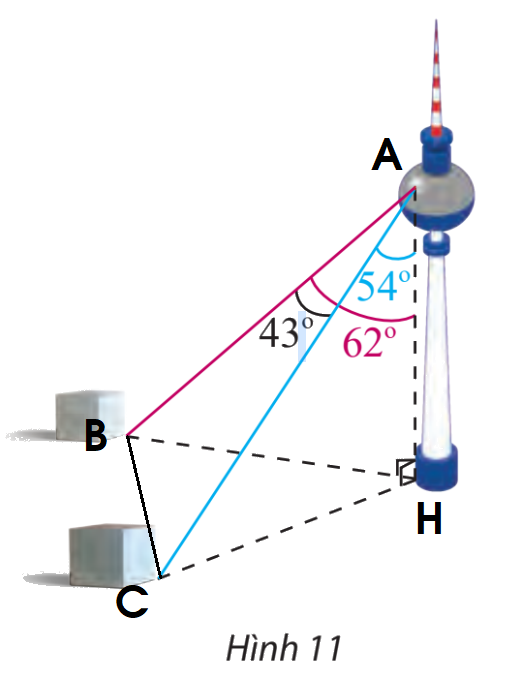
Bước 1: Kí hiệu các điểm A, B, C, H như hình trên.
Bước 2: Tính AB, AC bằng cách gắn vào tam giác ABH và ACH.
Bước 3: Áp dụng định lí cosin cho tam giác ABC: \(B{C^2} = A{B^2} + A{C^2} - 2.AB.AC.\cos A\)
Lời giải chi tiết
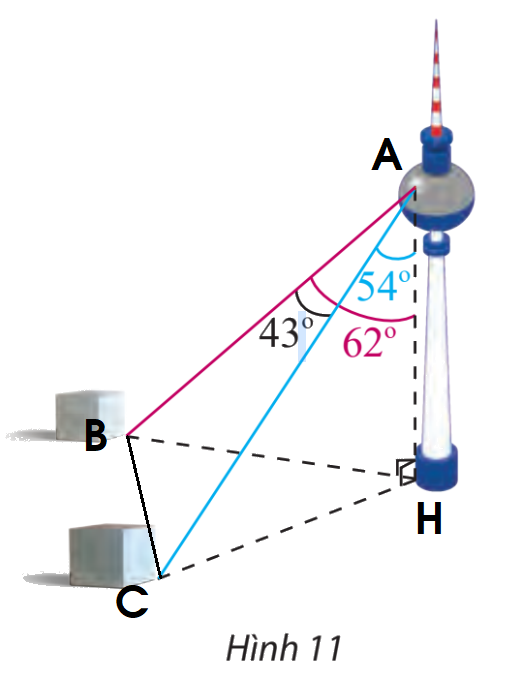
Gọi các điểm A, B, C, H như hình trên.
Xét tam giác ABH ta có:
\(AH = 352,\;\widehat {BAH} = {62^ \circ }\)
Mà \(\cos \widehat {BAH} = \frac{{AH}}{{AB}} \Rightarrow AB = 352 : \cos {62^ \circ } \approx 749,78\)
Tương tự, ta có: \(\cos \widehat {CAH} = \frac{{AH}}{{AC}} \Rightarrow AC = 352:\cos {54^ \circ } \approx 598,86\)
Áp dụng định lí cosin cho tam giác ABC, ta có:
\(\begin{array}{l}B{C^2} = A{B^2} + A{C^2} - 2.AB.AC.\cos A\\ \Leftrightarrow B{C^2} = {749,78^2} + {598,86^2} - 2.749,78.598,86.\cos {43^ \circ }\\ \Rightarrow BC \approx 513,84\end{array}\)
Vậy khoảng cách giữa hai cột mốc này là 513,84 m.
Bài 6 trang 78 SGK Toán 10 tập 1 – Chân trời sáng tạo thuộc chương trình học về Vectơ trong mặt phẳng. Bài tập này yêu cầu học sinh vận dụng kiến thức về các phép toán vectơ, đặc biệt là phép cộng, trừ vectơ và phép nhân vectơ với một số thực để giải quyết các bài toán cụ thể.
Bài 6 thường bao gồm các dạng bài tập sau:
Để giải quyết hiệu quả bài 6 trang 78 SGK Toán 10 tập 1 – Chân trời sáng tạo, học sinh cần nắm vững các kiến thức sau:
(Phần này sẽ trình bày lời giải chi tiết cho từng câu hỏi trong bài 6. Ví dụ:)
Lời giải:
Vectơ a + b = (1 + (-3); 2 + 4) = (-2; 6)
Lời giải:
Vectơ k.a = (3 * 2; 3 * (-1)) = (6; -3)
Để củng cố kiến thức, các em có thể tự giải các bài tập tương tự sau:
Khi giải bài tập về vectơ, các em cần chú ý:
Hy vọng với lời giải chi tiết và phương pháp giải bài tập được trình bày trong bài viết này, các em học sinh sẽ tự tin hơn khi giải bài 6 trang 78 SGK Toán 10 tập 1 – Chân trời sáng tạo và các bài tập tương tự. Chúc các em học tập tốt!