Tích vô hướng của hai vecto là một khái niệm quan trọng trong chương trình Toán 10 Chương trình Công nghệ. Nó không chỉ là công cụ để giải quyết các bài toán hình học mà còn là nền tảng cho nhiều kiến thức nâng cao hơn trong các lớp học tiếp theo.
Tại giaitoan.edu.vn, chúng tôi cung cấp bài học chi tiết, dễ hiểu về lý thuyết tích vô hướng, kèm theo các ví dụ minh họa và bài tập thực hành để giúp bạn nắm vững kiến thức một cách hiệu quả.
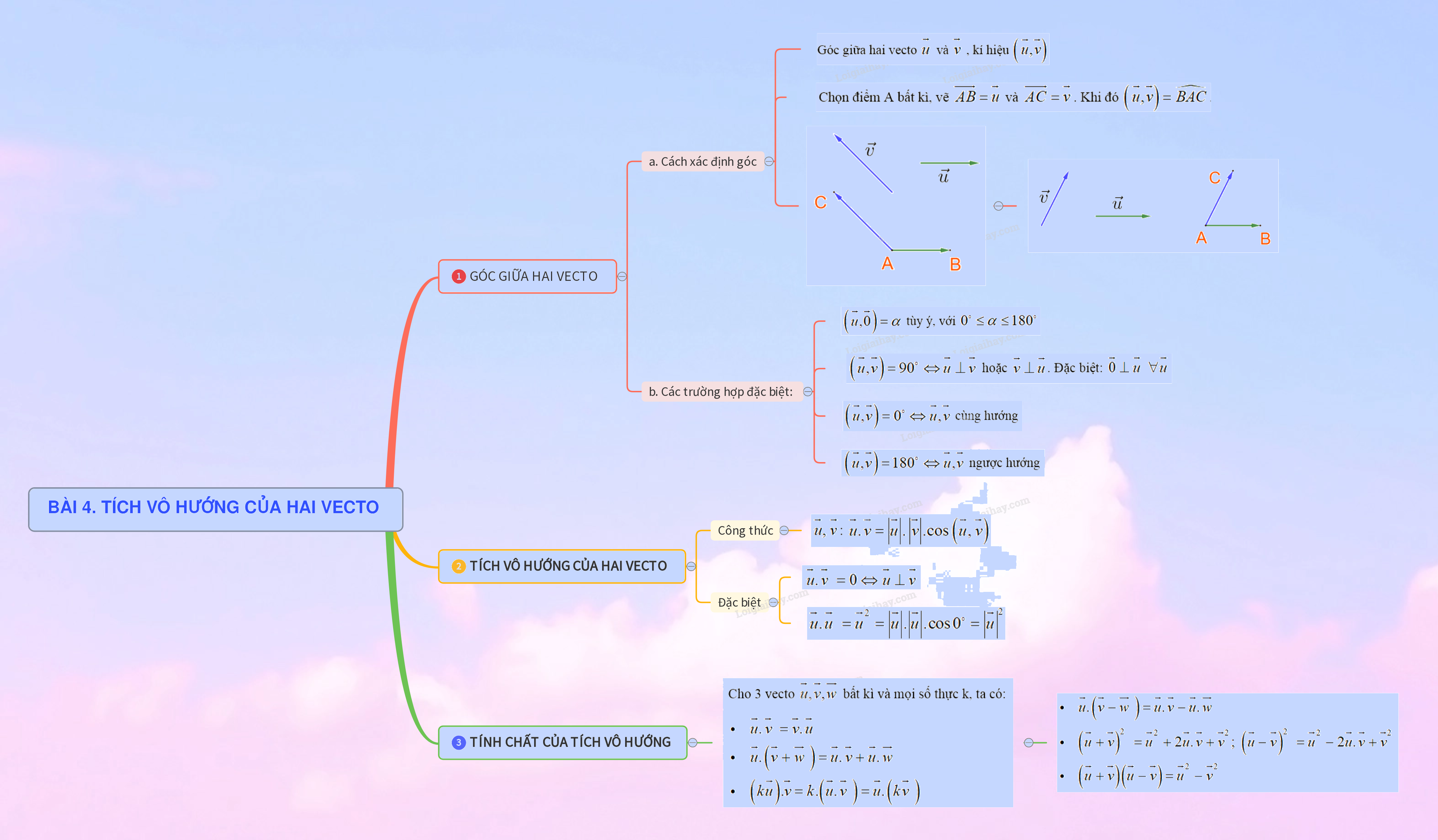
1. GÓC GIỮA HAI VECTO
1. GÓC GIỮA HAI VECTO
Cho hai vecto \(\overrightarrow u \) và \(\overrightarrow v \) khác \(\overrightarrow 0 \). Góc giữa hai vecto \(\overrightarrow u \) và \(\overrightarrow v \) , kí hiệu \(\left( {\;\overrightarrow u ,\overrightarrow v } \right)\)
a) Cách xác định góc:
Chọn điểm A bất kì, vẽ \(\overrightarrow {AB} = \overrightarrow u \) và \(\overrightarrow {AC} = \overrightarrow v \). Khi đó \(\left( {\;\overrightarrow u ,\overrightarrow v } \right) = \widehat {BAC}\).
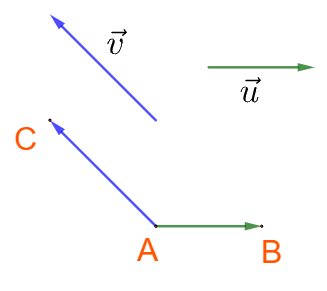
b) Các trường hợp đặc biệt:
+) \(\left( {\;\overrightarrow u ,\overrightarrow 0 } \right) = \alpha \) tùy ý, với \({0^ \circ } \le \alpha \le {180^ \circ }\)
+) \(\left( {\;\overrightarrow u ,\overrightarrow v } \right) = {90^ \circ } \Leftrightarrow \overrightarrow u \bot \overrightarrow v \) hoặc \(\overrightarrow v \bot \overrightarrow u \). Đặc biệt: \(\overrightarrow 0 \bot \overrightarrow u \;\;\forall \overrightarrow u \;\)
+) \(\left( {\;\overrightarrow u ,\overrightarrow v } \right) = {0^ \circ } \Leftrightarrow \overrightarrow u ,\overrightarrow v \) cùng hướng
+) \(\left( {\;\overrightarrow u ,\overrightarrow v } \right) = {180^ \circ } \Leftrightarrow \overrightarrow u ,\overrightarrow v \) ngược hướng
2. TÍCH VÔ HƯỚNG CỦA HAI VECTO
+) Tích vô hướng của hai vecto \(\overrightarrow u ,\;\overrightarrow v \): \(\overrightarrow u .\;\overrightarrow v = \left| {\overrightarrow u } \right|.\;\left| {\overrightarrow v } \right|.\cos \;\left( {\overrightarrow u ,\;\overrightarrow v } \right)\)
+) \(\overrightarrow u .\;\overrightarrow v \;\; = 0 \Leftrightarrow \overrightarrow u \bot \;\overrightarrow v \;\;\)
+) \(\overrightarrow u .\;\overrightarrow u \;\; = {\overrightarrow u ^2} = \left| {\overrightarrow u } \right|.\left| {\overrightarrow u } \right|.\cos {0^ \circ } = {\left| {\overrightarrow u } \right|^2}\)
3. TÍNH CHẤT CỦA TÍCH VÔ HƯỚNG
Cho 3 vecto \(\overrightarrow u ,\overrightarrow v ,\overrightarrow w \) bất kì và mọi số thực k, ta có:
\(\begin{array}{l}\overrightarrow u .\;\overrightarrow v \;\; = \overrightarrow v .\;\overrightarrow u \;\\\overrightarrow u .\;\left( {\overrightarrow v + \overrightarrow w \;} \right)\; = \overrightarrow u .\;\overrightarrow v \; + \overrightarrow u .\;\overrightarrow w \;\\\left( {k\overrightarrow u } \right).\overrightarrow v = k.\left( {\overrightarrow u .\;\overrightarrow v \;} \right) = \overrightarrow u .\;\left( {k\overrightarrow v \;} \right)\end{array}\)
Hệ quả
\(\begin{array}{l}\overrightarrow u .\;\left( {\overrightarrow v - \overrightarrow w \;} \right)\; = \overrightarrow u .\;\overrightarrow v \; - \overrightarrow u .\;\overrightarrow w \\{\left( {\overrightarrow u + \overrightarrow v } \right)^2}\;\; = {\overrightarrow u ^2} + 2\overrightarrow u .\;\overrightarrow v \; + \;{\overrightarrow v ^2};\;\;{\left( {\overrightarrow u - \overrightarrow v } \right)^2}\;\; = {\overrightarrow u ^2} - 2\overrightarrow u .\;\overrightarrow v \; + \;{\overrightarrow v ^2}\\\left( {\overrightarrow u + \overrightarrow v } \right)\left( {\overrightarrow u - \overrightarrow v } \right) = {\overrightarrow u ^2} - {\overrightarrow v ^2}\end{array}\)
Tích vô hướng của hai vecto là một phép toán cơ bản trong hình học vectơ, đóng vai trò quan trọng trong việc giải quyết nhiều bài toán liên quan đến góc giữa hai vectơ, độ dài vectơ, và các ứng dụng trong vật lý. Bài viết này sẽ trình bày chi tiết lý thuyết tích vô hướng của hai vectơ theo chương trình SGK Toán 10 CTST.
Cho hai vectơ a và b khác vectơ 0. Tích vô hướng của a và b, ký hiệu là a.b, là một số thực được tính theo công thức:
a.b = |a||b|cos(θ)
Trong đó:
Trong mặt phẳng tọa độ, cho hai vectơ a = (x1; y1) và b = (x2; y2). Tích vô hướng của a và b được tính bằng công thức:
a.b = x1x2 + y1y2
Bài 1: Cho a = (2; -3) và b = (-1; 4). Tính a.b.
Giải:a.b = (2)(-1) + (-3)(4) = -2 - 12 = -14
Bài 2: Cho hai vectơ a và b có độ dài lần lượt là 3 và 5, và góc giữa chúng là 60°. Tính a.b.
Giải:a.b = |a||b|cos(60°) = 3 * 5 * (1/2) = 7.5
Lý thuyết tích vô hướng của hai vectơ là một công cụ mạnh mẽ trong hình học và vật lý. Việc nắm vững định nghĩa, tính chất và ứng dụng của tích vô hướng sẽ giúp bạn giải quyết hiệu quả các bài toán liên quan. Hãy luyện tập thường xuyên để củng cố kiến thức và nâng cao kỹ năng giải toán.