Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 của giaitoan.edu.vn. Trong bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 3 trang 70, 71, 72 sách giáo khoa Toán 10 tập 1 chương trình Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong học tập.
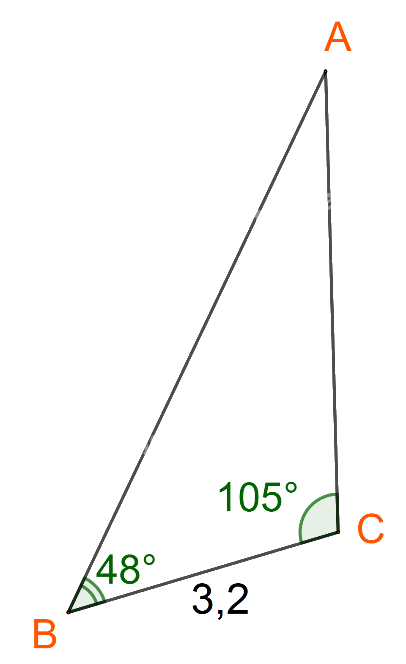
Tính diện tích một cánh buồm hình tam giác. Biết cách buồm đó có chiều dài một cạnh là 3,2 m và hai góc kề cách đó có số đo là 48 và 105) (Hình 12).
Tính diện tích tam giác ABC và bán kính đường tròn ngoại tiếp tam giác ABC trong các trường hợp sau:
a) Các cạnh \(b = 14,c = 35\) và \(\widehat A = {60^o}\)
b) Các cạnh \(a = 4,b = 5,c = 3\)
Phương pháp giải:
a) Áp dụng công thức: \(S = \frac{1}{2}bc\sin A\)
b) Áp dụng công thức Heron \(S = \sqrt {p(p - a)(p - b)(p - c)} \)
Lời giải chi tiết:
a) Áp dụng công thức: \(S = \frac{1}{2}bc\sin A\), ta có:
\(S = \frac{1}{2}.14.35.\sin {60^o} = \frac{1}{2}.14.35.\frac{{\sqrt 3 }}{2} \approx 212,2\)
Áp dụng đl cosin, ta có: \({a^2} = {b^2} + {c^2} - 2bc.\cos A\)
\(\begin{array}{l} \Rightarrow {a^2} = {14^2} + {35^2} - 2.14.35.\cos {60^o} = 931\\ \Rightarrow a \approx 30,5\end{array}\)
\( \Rightarrow R = \frac{a}{{2\sin A}} = \frac{{30,5}}{{2\sin {{60}^o}}} \approx 17,6\)
b) Ta có: \(p = \frac{1}{2}.(4 + 5 + 3) = 6\)
Áp dụng công thức Heron, ta có:
\(S = \sqrt {p(p - a)(p - b)(p - c)} = \sqrt {6(6 - 4)(6 - 5)(6 - 3)} = 6.\)
Lại có: \(S = \frac{{abc}}{{4R}} \Rightarrow R = \frac{{abc}}{{4S}} = \frac{{4.5.3}}{{4.6}} = 2,5.\)
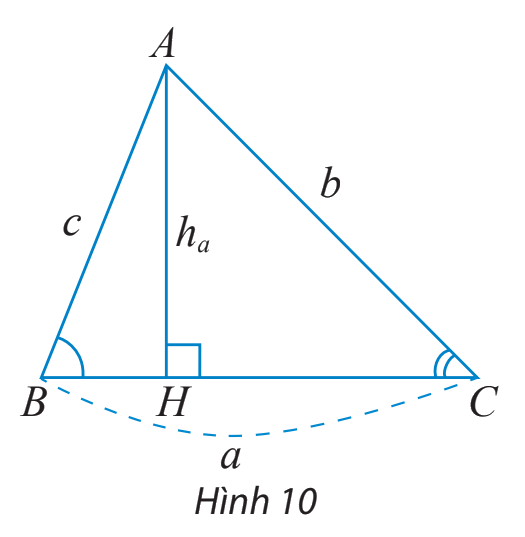
Cho tam giác ABC như Hình 10.
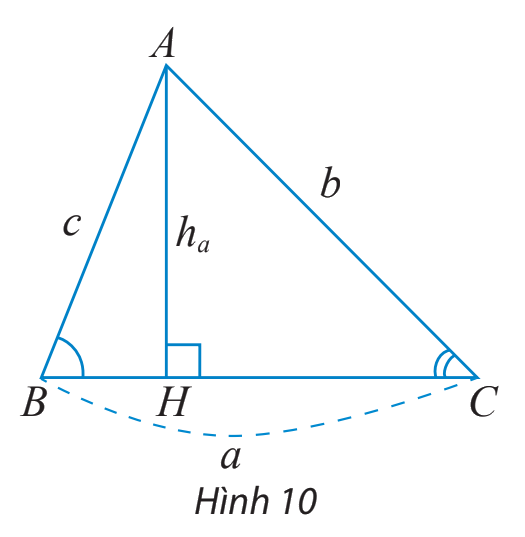
a) Viết công thức tính diện tích S của tam giác ABC theo a và \({h_a}\)
b) Tính \({h_a}\) theo b và sinC.
c) Dùng hai kết quả trên để chứng minh công thức \(S = \frac{1}{2}ab\sin C\)
d) Dùng định lí sin và kết quả ở câu c) để chứng minh công thức \(S = \frac{{abc}}{{4R}}\)
Lời giải chi tiết:
a) Diện tích S của tam giác ABC là: \(S = \frac{1}{2}a.{h_a}\)
b) Xét tam giác vuông AHC ta có: \(\sin C = \frac{{AH}}{{AC}} = \frac{{{h_a}}}{b}\)
\( \Rightarrow {h_a} = b.\sin C\)
c) Thay \({h_a} = b.\sin C\) vào công thức diện tích, ta được: \(S = \frac{1}{2}ab\sin C\)
d) Theo định lí sin ta có: \(\frac{c}{{\sin C}} = 2R \Rightarrow \sin C = \frac{c}{{2R}}\)
Thay vào công thức ở c) ta được: \(S = \frac{1}{2}ab\frac{c}{{2R}} = \frac{{abc}}{{4R}}.\)
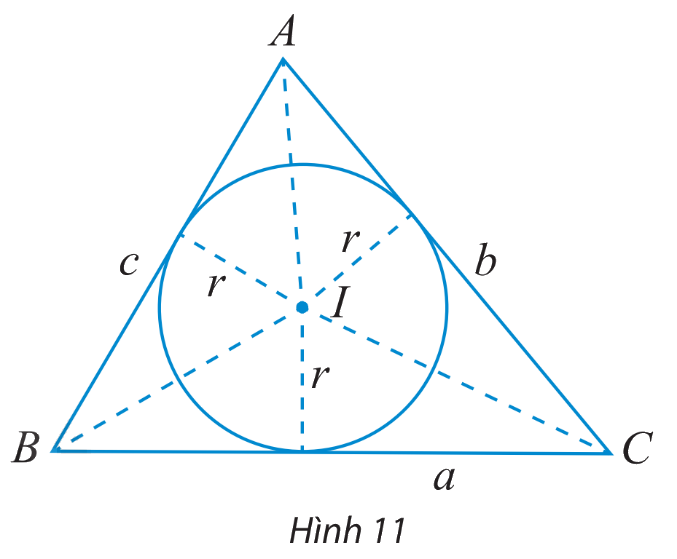
Cho tam giác ABC có BC = a, AC = b, AB = c và (I;r) là đường tròn nội tiếp tam giác (Hình 11).
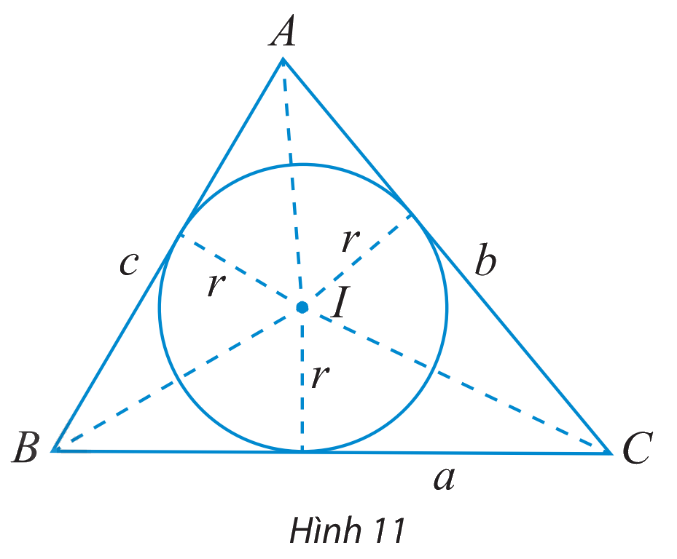
a) Tính diện tích các tam giác IBC, IAC, IAB theo r và a, b, c.
b) Dùng kết quả trên để chứng minh công thức tính diện tích tam giác ABC: \(S = \frac{{r(a + b + c)}}{2}\)
Lời giải chi tiết:
a) Diện tích \({S_1}\) của tam giác IAB là: \({S_1} = \frac{1}{2}r.AB = \frac{1}{2}r.c\)
Diện tích \({S_2}\) của tam giác IAC là: \({S_2} = \frac{1}{2}r.AC = \frac{1}{2}r.b\)
Diện tích \({S_3}\) của tam giác IBC là: \({S_3} = \frac{1}{2}r.BC = \frac{1}{2}r.a\)
b) Diện tích S của tam giác ABC là:
\(\begin{array}{l}S = {S_1} + {S_2} + {S_3} = \frac{1}{2}r.c + \frac{1}{2}r.b + \frac{1}{2}r.a = \frac{1}{2}r.(c + b + a)\\ \Leftrightarrow S = \frac{{r(a + b + c)}}{2}\end{array}\)
Tính diện tích một cánh buồm hình tam giác. Biết cách buồm đó có chiều dài một cạnh là 3,2 m và hai góc kề cách đó có số đo là \({48^o}\) và \({105^o}\) (Hình 12).

Phương pháp giải:
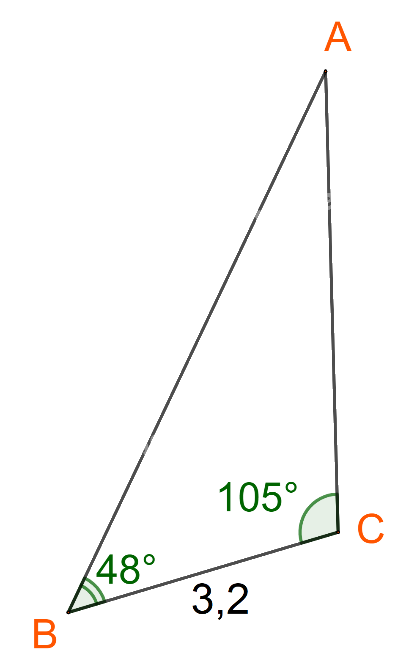
Bước 1: Áp dụng định lí sin tính AC.
Bước 2: Tính diện tích tam giác ABC bằng công thức \(S = \frac{1}{2}ab\sin C\)
Lời giải chi tiết:
Kí hiệu các điểm A, B, C như hình dưới
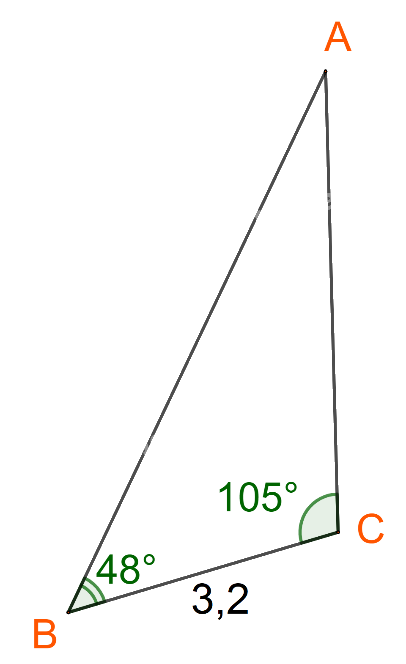
Đặt \(AB = c,AC = b,BC = a.\)
Ta có: \(BC = 3,2;\widehat A = {180^o} - ({48^o} + {105^o}) = {27^o}\)
Áp dụng định lí sin, ta có:
\(\frac{b}{{\sin B}} = \frac{a}{{\sin A}} \Rightarrow AC = b = \frac{{a.\sin B}}{{\sin A}} = \frac{{3,2.\sin {{48}^o}}}{{\sin {{27}^o}}} \approx 5,24(m)\)
Áp dụng công thức \(S = \frac{1}{2}ab\sin C\) ta có:
\(S = \frac{1}{2}.3,2.5,24\sin {105^o} \approx 8,1({m^2})\)
Cho tam giác ABC như Hình 10.
a) Viết công thức tính diện tích S của tam giác ABC theo a và \({h_a}\)
b) Tính \({h_a}\) theo b và sinC.
c) Dùng hai kết quả trên để chứng minh công thức \(S = \frac{1}{2}ab\sin C\)
d) Dùng định lí sin và kết quả ở câu c) để chứng minh công thức \(S = \frac{{abc}}{{4R}}\)
Lời giải chi tiết:
a) Diện tích S của tam giác ABC là: \(S = \frac{1}{2}a.{h_a}\)
b) Xét tam giác vuông AHC ta có: \(\sin C = \frac{{AH}}{{AC}} = \frac{{{h_a}}}{b}\)
\( \Rightarrow {h_a} = b.\sin C\)
c) Thay \({h_a} = b.\sin C\) vào công thức diện tích, ta được: \(S = \frac{1}{2}ab\sin C\)
d) Theo định lí sin ta có: \(\frac{c}{{\sin C}} = 2R \Rightarrow \sin C = \frac{c}{{2R}}\)
Thay vào công thức ở c) ta được: \(S = \frac{1}{2}ab\frac{c}{{2R}} = \frac{{abc}}{{4R}}.\)
Cho tam giác ABC có BC = a, AC = b, AB = c và (I;r) là đường tròn nội tiếp tam giác (Hình 11).
a) Tính diện tích các tam giác IBC, IAC, IAB theo r và a, b, c.
b) Dùng kết quả trên để chứng minh công thức tính diện tích tam giác ABC: \(S = \frac{{r(a + b + c)}}{2}\)
Lời giải chi tiết:
a) Diện tích \({S_1}\) của tam giác IAB là: \({S_1} = \frac{1}{2}r.AB = \frac{1}{2}r.c\)
Diện tích \({S_2}\) của tam giác IAC là: \({S_2} = \frac{1}{2}r.AC = \frac{1}{2}r.b\)
Diện tích \({S_3}\) của tam giác IBC là: \({S_3} = \frac{1}{2}r.BC = \frac{1}{2}r.a\)
b) Diện tích S của tam giác ABC là:
\(\begin{array}{l}S = {S_1} + {S_2} + {S_3} = \frac{1}{2}r.c + \frac{1}{2}r.b + \frac{1}{2}r.a = \frac{1}{2}r.(c + b + a)\\ \Leftrightarrow S = \frac{{r(a + b + c)}}{2}\end{array}\)
Tính diện tích tam giác ABC và bán kính đường tròn ngoại tiếp tam giác ABC trong các trường hợp sau:
a) Các cạnh \(b = 14,c = 35\) và \(\widehat A = {60^o}\)
b) Các cạnh \(a = 4,b = 5,c = 3\)
Phương pháp giải:
a) Áp dụng công thức: \(S = \frac{1}{2}bc\sin A\)
b) Áp dụng công thức Heron \(S = \sqrt {p(p - a)(p - b)(p - c)} \)
Lời giải chi tiết:
a) Áp dụng công thức: \(S = \frac{1}{2}bc\sin A\), ta có:
\(S = \frac{1}{2}.14.35.\sin {60^o} = \frac{1}{2}.14.35.\frac{{\sqrt 3 }}{2} \approx 212,2\)
Áp dụng đl cosin, ta có: \({a^2} = {b^2} + {c^2} - 2bc.\cos A\)
\(\begin{array}{l} \Rightarrow {a^2} = {14^2} + {35^2} - 2.14.35.\cos {60^o} = 931\\ \Rightarrow a \approx 30,5\end{array}\)
\( \Rightarrow R = \frac{a}{{2\sin A}} = \frac{{30,5}}{{2\sin {{60}^o}}} \approx 17,6\)
b) Ta có: \(p = \frac{1}{2}.(4 + 5 + 3) = 6\)
Áp dụng công thức Heron, ta có:
\(S = \sqrt {p(p - a)(p - b)(p - c)} = \sqrt {6(6 - 4)(6 - 5)(6 - 3)} = 6.\)
Lại có: \(S = \frac{{abc}}{{4R}} \Rightarrow R = \frac{{abc}}{{4S}} = \frac{{4.5.3}}{{4.6}} = 2,5.\)
Tính diện tích một cánh buồm hình tam giác. Biết cách buồm đó có chiều dài một cạnh là 3,2 m và hai góc kề cách đó có số đo là \({48^o}\) và \({105^o}\) (Hình 12).

Phương pháp giải:
Bước 1: Áp dụng định lí sin tính AC.
Bước 2: Tính diện tích tam giác ABC bằng công thức \(S = \frac{1}{2}ab\sin C\)
Lời giải chi tiết:
Kí hiệu các điểm A, B, C như hình dưới
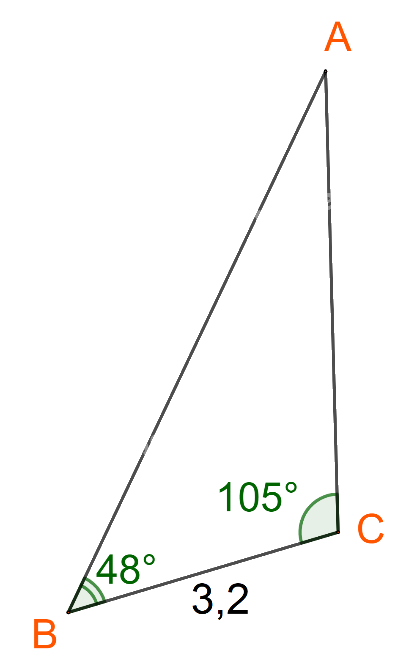
Đặt \(AB = c,AC = b,BC = a.\)
Ta có: \(BC = 3,2;\widehat A = {180^o} - ({48^o} + {105^o}) = {27^o}\)
Áp dụng định lí sin, ta có:
\(\frac{b}{{\sin B}} = \frac{a}{{\sin A}} \Rightarrow AC = b = \frac{{a.\sin B}}{{\sin A}} = \frac{{3,2.\sin {{48}^o}}}{{\sin {{27}^o}}} \approx 5,24(m)\)
Áp dụng công thức \(S = \frac{1}{2}ab\sin C\) ta có:
\(S = \frac{1}{2}.3,2.5,24\sin {105^o} \approx 8,1({m^2})\)
Mục 3 của SGK Toán 10 tập 1 chương trình Chân trời sáng tạo tập trung vào các kiến thức về vectơ, bao gồm các khái niệm cơ bản, các phép toán trên vectơ, và ứng dụng của vectơ trong hình học. Việc nắm vững các kiến thức này là nền tảng quan trọng để học tốt các chương trình Toán học ở các lớp trên.
Để giải tốt các bài tập về vectơ, các em cần nắm vững các kiến thức cơ bản và áp dụng linh hoạt các phương pháp sau:
Lời giải: Để giải bài tập này, ta cần sử dụng công thức cộng vectơ. Ta có: ...
Lời giải: Để tìm tọa độ của vectơ, ta cần sử dụng công thức tính tọa độ của vectơ khi biết tọa độ của điểm gốc và điểm cuối. Ta có: ...
Lời giải: Để chứng minh đẳng thức vectơ, ta cần sử dụng các phép biến đổi vectơ để đưa về dạng đơn giản. Ta có: ...
Sau khi đã học xong lý thuyết và giải các bài tập trong SGK, các em nên làm thêm các bài tập luyện tập để củng cố kiến thức. Các em có thể tìm các bài tập luyện tập trên các trang web học toán online, hoặc trong các sách bài tập Toán 10.
Việc luyện tập thường xuyên sẽ giúp các em nắm vững kiến thức và kỹ năng giải toán về vectơ.
Hy vọng rằng bài viết này đã cung cấp cho các em những kiến thức và phương pháp giải bài tập hiệu quả cho mục 3 trang 70, 71, 72 SGK Toán 10 tập 1 chương trình Chân trời sáng tạo. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!