Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 1 trang 98, 99 SGK Toán 10 tập 1 chương trình Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập một cách khoa học và hiệu quả.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, tự tin giải quyết các bài toán Toán 10 và đạt kết quả tốt nhất trong học tập.
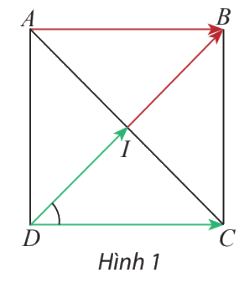
Cho hình vuông ABCD có tâm I (Hình 1). Cho tam giác đều ABC có H là trung điểm của cạnh BC. Tìm các góc:
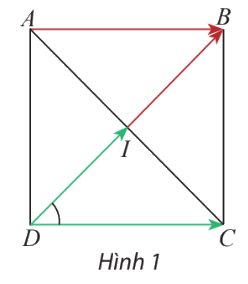
Cho hình vuông ABCD có tâm I (Hình 1).
a) Tính \(\widehat {IDC}\).
b) Tìm hai vectơ cùng có điểm đầu là D và điểm cuối lần lượt là I và C
c) Tìm hai vectơ có điểm đầu là D và lần lượt bằng vectơ \(\overrightarrow {IB} \)và \(\overrightarrow {AB} \)
Lời giải chi tiết:
a) I là tâm của ABCD, suy ra \(\widehat {IDC} = 45^\circ \)
b) Vectơ có điểm đầu là D và điểm cuối là I là \(\overrightarrow {DI} \)
Vectơ có điểm đầu là D và điểm cuối là C là \(\overrightarrow {DC} \)
c) Vectơ có điểm đầu là D và bằng vectơ \(\overrightarrow {IB} \) là \(\overrightarrow {DI} \)
Vectơ có điểm đầu là D và bằng vectơ \(\overrightarrow {AB} \) là \(\overrightarrow {DC} \)
Cho tam giác đều ABC có H là trung điểm của cạnh BC. Tìm các góc:
\(\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right),\left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right),\left( {\overrightarrow {AH} ,\overrightarrow {BC} } \right),\left( {\overrightarrow {BH} ,\overrightarrow {BC} } \right),\left( {\overrightarrow {HB} ,\overrightarrow {BC} } \right)\).
Phương pháp giải:
Bước 1: Xác định hai vectơ cần tìm góc
Bước 2: Đưa 2 vectơ về cùng điểm đầu (chung gốc)
Bước 3: Xác định góc giữa 2 vectơ, chẳng hạn: \(\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \widehat {BAC}\)
Lời giải chi tiết:
+) \(\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \widehat {ABC} = 60^\circ \)
+) Dựng hình bình hành ABCD, ta có: \(\overrightarrow {AD} = \overrightarrow {BC} \)
\( \Rightarrow \left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right) = \left( {\overrightarrow {AB} ,\overrightarrow {AD} } \right) = \widehat {BAD} = 120^\circ \)
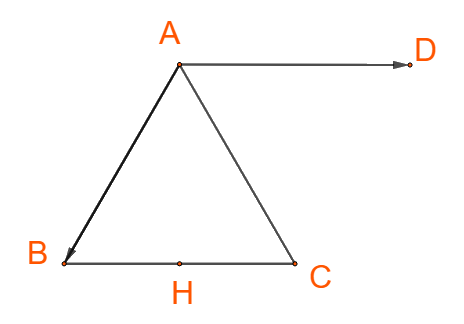
+), Ta có: ABC là tam giác đều, H là trung điểm BC nên \(AH \bot BC\)
\(\left( {\overrightarrow {AH} ,\overrightarrow {BC} } \right) = \left( {\overrightarrow {AH} ,\overrightarrow {AD} } \right) = \widehat {HAD} = 90^\circ \)
+) Hai vectơ \(\overrightarrow {BH} \) và \(\overrightarrow {BC} \)cùng hướng nên \(\left( {\overrightarrow {BH} ,\overrightarrow {BC} } \right) = 0^\circ \)
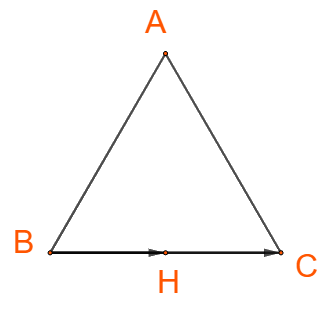
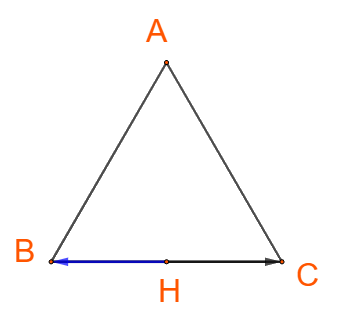
+) Hai vectơ \(\overrightarrow {HB} \) và \(\overrightarrow {BC} \)ngược hướng nên \(\left( {\overrightarrow {HB} ,\overrightarrow {BC} } \right) = 180^\circ \)
Cho hình vuông ABCD có tâm I (Hình 1).
a) Tính \(\widehat {IDC}\).
b) Tìm hai vectơ cùng có điểm đầu là D và điểm cuối lần lượt là I và C
c) Tìm hai vectơ có điểm đầu là D và lần lượt bằng vectơ \(\overrightarrow {IB} \)và \(\overrightarrow {AB} \)
Lời giải chi tiết:
a) I là tâm của ABCD, suy ra \(\widehat {IDC} = 45^\circ \)
b) Vectơ có điểm đầu là D và điểm cuối là I là \(\overrightarrow {DI} \)
Vectơ có điểm đầu là D và điểm cuối là C là \(\overrightarrow {DC} \)
c) Vectơ có điểm đầu là D và bằng vectơ \(\overrightarrow {IB} \) là \(\overrightarrow {DI} \)
Vectơ có điểm đầu là D và bằng vectơ \(\overrightarrow {AB} \) là \(\overrightarrow {DC} \)
Cho tam giác đều ABC có H là trung điểm của cạnh BC. Tìm các góc:
\(\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right),\left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right),\left( {\overrightarrow {AH} ,\overrightarrow {BC} } \right),\left( {\overrightarrow {BH} ,\overrightarrow {BC} } \right),\left( {\overrightarrow {HB} ,\overrightarrow {BC} } \right)\).
Phương pháp giải:
Bước 1: Xác định hai vectơ cần tìm góc
Bước 2: Đưa 2 vectơ về cùng điểm đầu (chung gốc)
Bước 3: Xác định góc giữa 2 vectơ, chẳng hạn: \(\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \widehat {BAC}\)
Lời giải chi tiết:
+) \(\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \widehat {ABC} = 60^\circ \)
+) Dựng hình bình hành ABCD, ta có: \(\overrightarrow {AD} = \overrightarrow {BC} \)
\( \Rightarrow \left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right) = \left( {\overrightarrow {AB} ,\overrightarrow {AD} } \right) = \widehat {BAD} = 120^\circ \)
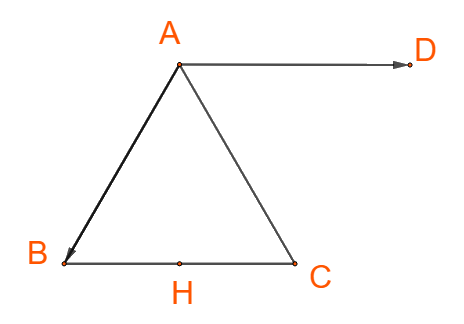
+), Ta có: ABC là tam giác đều, H là trung điểm BC nên \(AH \bot BC\)
\(\left( {\overrightarrow {AH} ,\overrightarrow {BC} } \right) = \left( {\overrightarrow {AH} ,\overrightarrow {AD} } \right) = \widehat {HAD} = 90^\circ \)
+) Hai vectơ \(\overrightarrow {BH} \) và \(\overrightarrow {BC} \)cùng hướng nên \(\left( {\overrightarrow {BH} ,\overrightarrow {BC} } \right) = 0^\circ \)
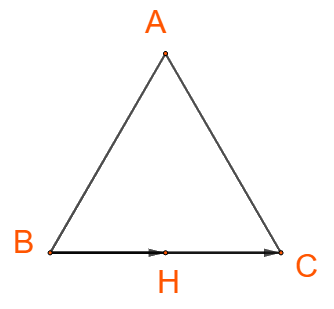
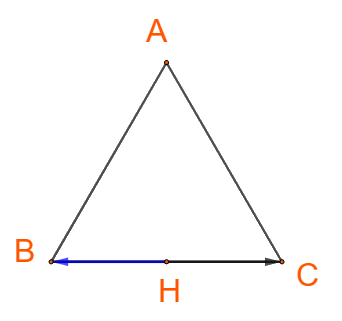
+) Hai vectơ \(\overrightarrow {HB} \) và \(\overrightarrow {BC} \)ngược hướng nên \(\left( {\overrightarrow {HB} ,\overrightarrow {BC} } \right) = 180^\circ \)
Mục 1 của chương trình Toán 10 tập 1 Chân trời sáng tạo tập trung vào việc giới thiệu các khái niệm cơ bản về tập hợp, các phép toán trên tập hợp và các tính chất của chúng. Đây là nền tảng quan trọng để học sinh có thể tiếp cận các kiến thức phức tạp hơn trong các chương tiếp theo.
Bài tập mục 1 trang 98, 99 SGK Toán 10 tập 1 Chân trời sáng tạo bao gồm các dạng bài tập khác nhau, yêu cầu học sinh vận dụng kiến thức đã học để:
Để giải bài tập này, học sinh cần nắm vững định nghĩa về tập hợp và cách xác định các phần tử của tập hợp. Ví dụ, nếu tập hợp A là tập hợp các số tự nhiên chẵn nhỏ hơn 10, thì các phần tử của tập hợp A là: {0, 2, 4, 6, 8}.
Sơ đồ Venn là một công cụ trực quan giúp biểu diễn các tập hợp và mối quan hệ giữa chúng. Để biểu diễn tập hợp bằng sơ đồ Venn, học sinh cần xác định các tập hợp con và các phần tử chung của chúng.
Các phép toán trên tập hợp (hợp, giao, hiệu, phần bù) là các phép toán cơ bản trong lý thuyết tập hợp. Để thực hiện các phép toán này, học sinh cần nắm vững định nghĩa và các quy tắc liên quan.
Ví dụ:
Để chứng minh các đẳng thức liên quan đến tập hợp, học sinh cần sử dụng các quy tắc logic và các tính chất của tập hợp. Ví dụ, để chứng minh A ∪ B = B ∪ A, học sinh cần chứng minh rằng mọi phần tử thuộc A ∪ B đều thuộc B ∪ A và ngược lại.
Các bài toán ứng dụng tập hợp vào thực tế giúp học sinh hiểu rõ hơn về tầm quan trọng của lý thuyết tập hợp trong đời sống. Để giải các bài toán này, học sinh cần phân tích đề bài, xác định các tập hợp liên quan và vận dụng kiến thức đã học để tìm ra lời giải.
Hy vọng rằng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải quyết các bài tập mục 1 trang 98, 99 SGK Toán 10 tập 1 Chân trời sáng tạo một cách hiệu quả. Chúc các em học tập tốt!