Chào mừng bạn đến với bài học về Lý thuyết Bất phương trình bậc nhất hai ẩn, một phần quan trọng trong chương trình SGK Toán 10 Chân trời sáng tạo. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản nhất về bất phương trình, cách nhận biết, và các quy tắc giải.
Tại giaitoan.edu.vn, chúng tôi cam kết mang đến cho bạn trải nghiệm học toán online hiệu quả và thú vị. Hãy cùng bắt đầu khám phá thế giới của bất phương trình ngay bây giờ!
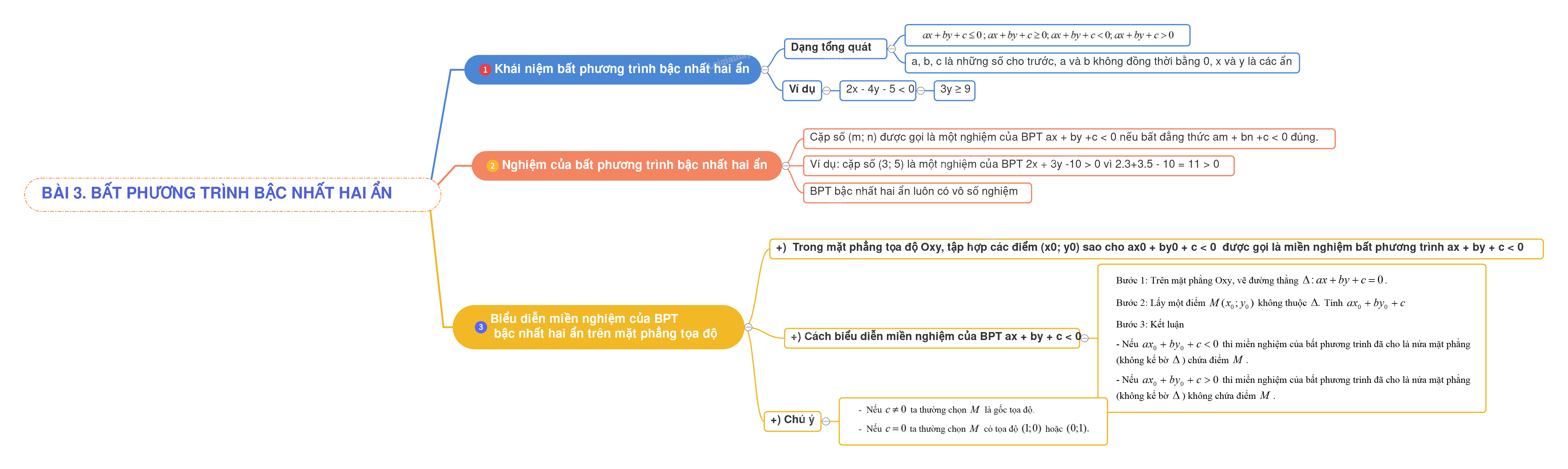
1. Khái niệm bất phương trình bậc nhất hai ẩn 2. Nghiệm của bất phương trình bậc nhất hai ẩn 3. Biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn
1. Khái niệm bất phương trình bậc nhất hai ẩn
+) Bất phương trình bậc nhất hai ẩn x, y là BPT có một trong các dạng
\(ax + by + c \le 0\;;ax + by + c \ge 0;ax + by + c < 0;ax + by + c > 0\) trong đó a, b, c là những số cho trước, a và b không đồng thời bằng 0, x và y là các ẩn.
Ví dụ: \(2x + 3y - 10 > 0\)
2. Nghiệm của bất phương trình bậc nhất hai ẩn
+) Mỗi cặp số \(({x_0};{y_0})\) thỏa mãn \(a{x_0} + b{y_0} + c\; < 0\) được gọi là một nghiệm của BPT đã cho.
Ví dụ: cặp số \((3;5)\) là một nghiệm của BPT \(2x + 3y - 10 > 0\) vì \(2.3 + 3.5 - 10 = 11 > 0\)
+) BPT bậc nhất hai ẩn luôn có vô số nghiệm.
3. Biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn
+) Trong mặt phẳng tọa độ Oxy, tập hợp các điểm \(({x_0};{y_0})\) sao cho \(a{x_0} + b{y_0} + c < 0\) được gọi là miền nghiệm của bất phương trình \(ax + by + c < 0\).
+) Biểu diễn miền nghiệm của BPT \(ax + by + c < 0\)
Bước 1: Trên mặt phẳng Oxy, vẽ đường thẳng \(\Delta :ax + by + c = 0\).
Bước 2: Lấy một điểm \(M({x_0};{y_0})\) không thuộc \(\Delta .\) Tính \(a{x_0} + b{y_0} + c\)
Bước 3: Kết luận
- Nếu \(a{x_0} + b{y_0} + c < 0\) thì miền nghiệm của bất phương trình đã cho là nửa mặt phẳng (không kể bờ \(\Delta \)) chứa điểm \(M\).
- Nếu \(a{x_0} + b{y_0} + c > 0\) thì miền nghiệm của bất phương trình đã cho là nửa mặt phẳng (không kể bờ \(\Delta \)) không chứa điểm \(M\).
* Chú ý:
- Nếu \(c \ne 0\) ta thường chọn \(M\) là gốc tọa độ.
- Nếu \(c = 0\) ta thường chọn \(M\) có tọa độ \((1;0)\) hoặc \((0;1).\)
Bất phương trình bậc nhất hai ẩn là một trong những chủ đề quan trọng trong chương trình Toán 10, đặc biệt là với bộ sách Chân trời sáng tạo. Việc nắm vững lý thuyết và kỹ năng giải quyết các bài toán liên quan đến bất phương trình này là nền tảng vững chắc cho các kiến thức toán học nâng cao hơn.
Bất phương trình bậc nhất hai ẩn là bất phương trình có dạng ax + by < c (hoặc ax + by ≤ c, ax + by > c, ax + by ≥ c), trong đó a, b, và c là các số thực, và a và b không đồng thời bằng 0. x và y là các ẩn số.
Tập nghiệm của bất phương trình bậc nhất hai ẩn là tập hợp tất cả các cặp số (x; y) thỏa mãn bất phương trình. Tập nghiệm này thường được biểu diễn bằng một nửa mặt phẳng trên mặt phẳng tọa độ.
Để biểu diễn hình học tập nghiệm của bất phương trình ax + by < c, ta thực hiện các bước sau:
Ví dụ 1: Giải bất phương trình 2x + y ≤ 4.
Giải:
Ví dụ 2: Giải bất phương trình x - 3y > 2.
Giải:
Để củng cố kiến thức, bạn có thể thực hành giải các bài tập sau:
Lý thuyết Bất phương trình bậc nhất hai ẩn là một phần quan trọng của chương trình Toán 10. Việc hiểu rõ định nghĩa, tập nghiệm, và các quy tắc giải sẽ giúp bạn tự tin giải quyết các bài toán liên quan. Hãy luyện tập thường xuyên để nắm vững kiến thức này nhé!