Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập Toán 10 tập 2 theo chương trình Chân trời sáng tạo. Bài viết này sẽ hướng dẫn bạn giải Hoạt động 3 trang 96 một cách dễ hiểu nhất.
Chúng tôi hiểu rằng việc tự học Toán đôi khi gặp nhiều khó khăn. Vì vậy, đội ngũ giaitoan.edu.vn đã biên soạn lời giải chi tiết, kèm theo các bước giải thích rõ ràng, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
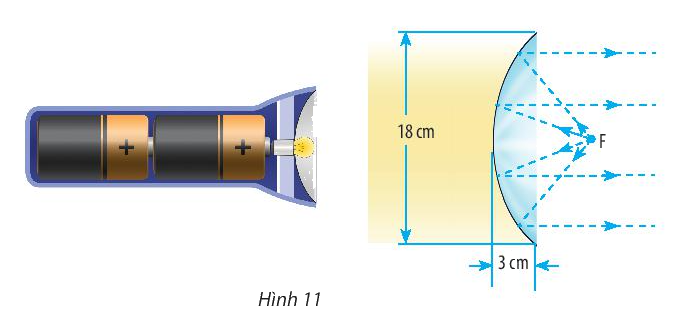
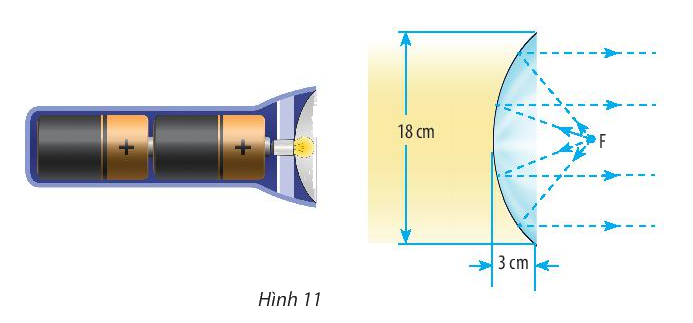
Thiết kế một chóa đèn có mặt cắt hình parabol với kích thước được cho trong hình sau:
Thiết kế một chóa đèn có mặt cắt hình parabol với kích thước được cho trong hình sau:
Phương pháp giải:
Bước 1: Giả sử phương trình của parabol
Bước 2: Từ kích thước giả thiết cho, xác định điểm nằm trên phương trình
Bước 3: Xác định phương trình parabol
Bước 4: Sử dụng Geogebra vẽ hình dạng mô phỏng chóa đèn
Lời giải chi tiết:
Chóa đèn có hình dạng parabol nên phương trình mô phỏng chóa đèn có dạng \({y^2} = 2px\)
Gắn hệ tọa độ Oxy vào chóa đèn với gốc tọa độ tại đỉnh chóa đèn, suy ta phương trình đó đi qua điểm có tọa độ (3; 9)
Thay tọa độ điểm (3; 9) vào phương trình \({y^2} = 2px\), ta có \({9^2} = 2p.3 \Rightarrow p = \frac{{27}}{2}\)
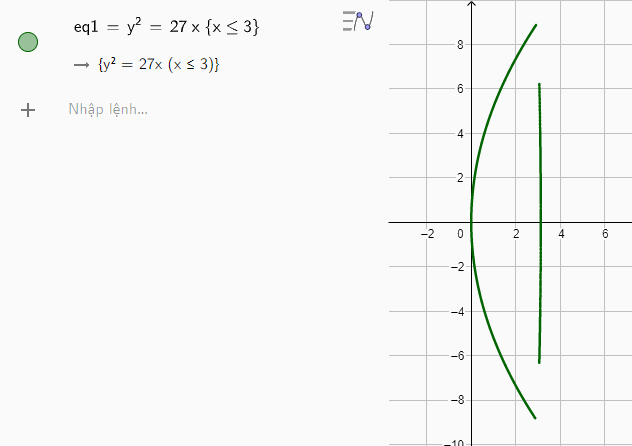
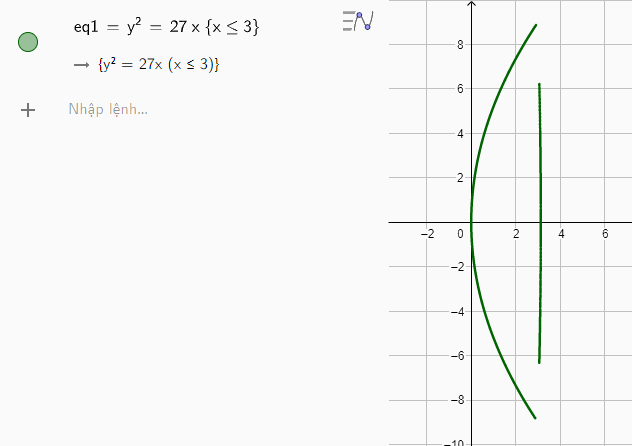
Suy ra phương trình mô tả chóa đèn là \({y^2} = 27x\) với \(x \le 3\)
Hình ảnh mô phỏng chóa đèn có dạng như hình dưới:
Vẽ các parabol sau:
a) \({y^2} = 16x\)
b) \({y^2} = x\)
c) \({y^2} = 32x\)
Phương pháp giải:
Bước 1: Khởi động phần mềm Geogebra
Bước 2: Nhập phương trình parabol \({y^2} = 2px\) theo cú pháp y^2 = 2px vào vùng nhập lệnh
Bước 3: Quan sát hình vẽ xuất hiện trên vùng làm việc
Lời giải chi tiết:
Thực hiện các bước đã nêu ở phương pháp ta có
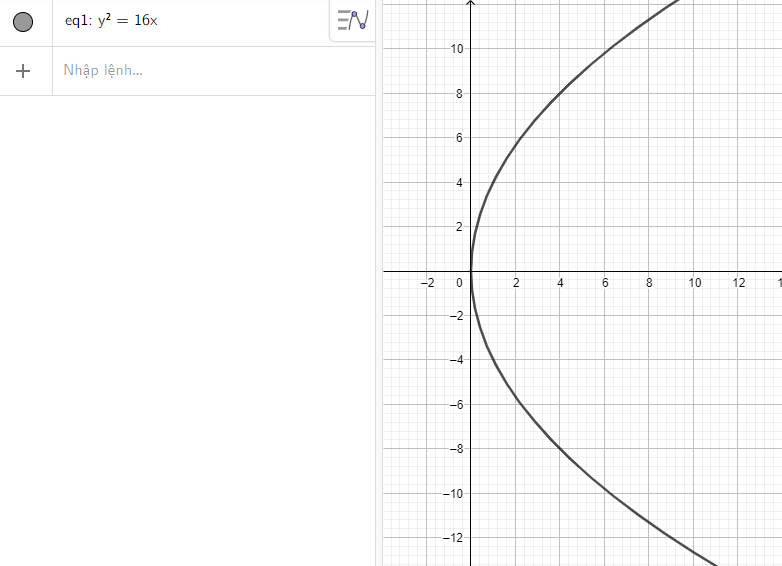
a) Nhập phương trình parabol theo cú pháp y^2 = 16x vào vùng nhập lệnh ta được hình parabol dưới đây:
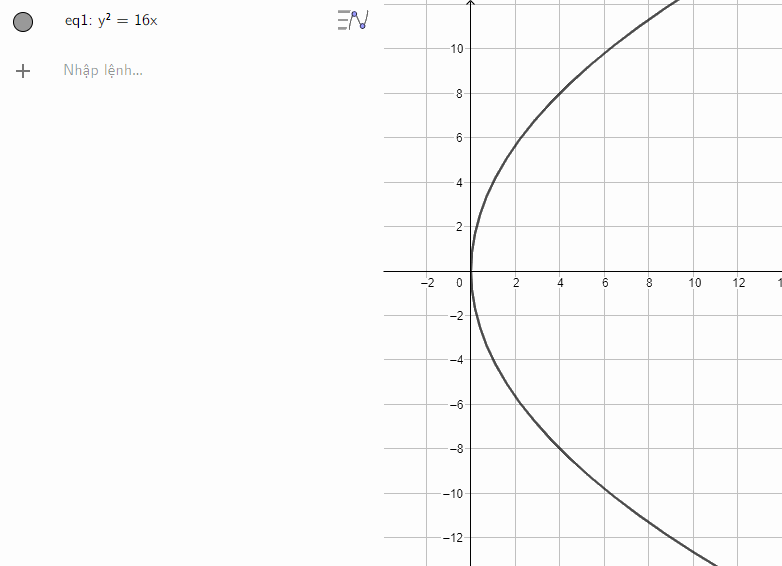
b) Nhập phương trình parabol theo cú pháp y^2 = x vào vùng nhập lệnh ta được hình parabol dưới đây:
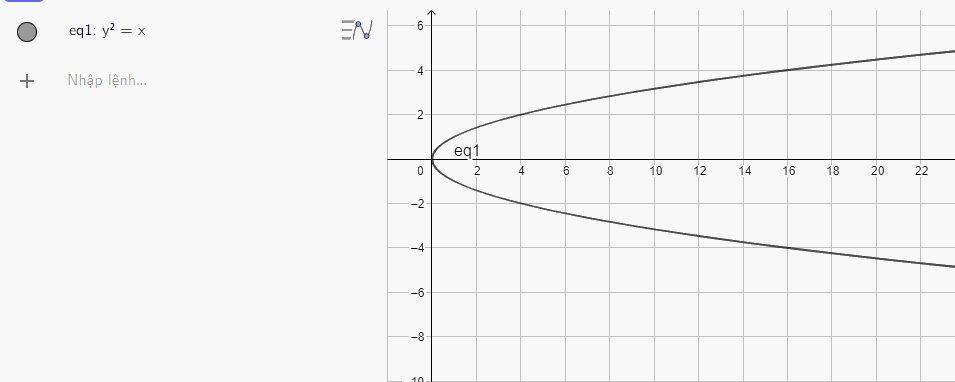
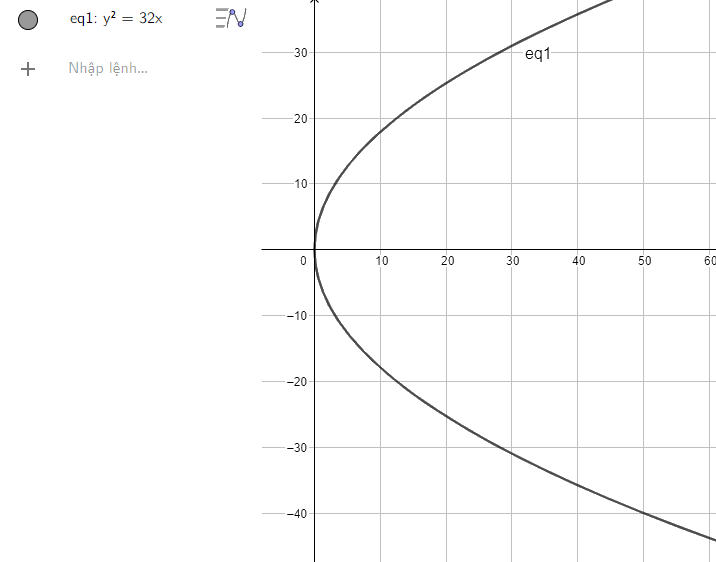
c) Nhập phương trình parabol theo cú pháp y^2 = 32x vào vùng nhập lệnh ta được hình parabol dưới đây:
Thiết kế một chóa đèn có mặt cắt hình parabol với kích thước được cho trong hình sau:
Phương pháp giải:
Bước 1: Giả sử phương trình của parabol
Bước 2: Từ kích thước giả thiết cho, xác định điểm nằm trên phương trình
Bước 3: Xác định phương trình parabol
Bước 4: Sử dụng Geogebra vẽ hình dạng mô phỏng chóa đèn
Lời giải chi tiết:
Chóa đèn có hình dạng parabol nên phương trình mô phỏng chóa đèn có dạng \({y^2} = 2px\)
Gắn hệ tọa độ Oxy vào chóa đèn với gốc tọa độ tại đỉnh chóa đèn, suy ta phương trình đó đi qua điểm có tọa độ (3; 9)
Thay tọa độ điểm (3; 9) vào phương trình \({y^2} = 2px\), ta có \({9^2} = 2p.3 \Rightarrow p = \frac{{27}}{2}\)
Suy ra phương trình mô tả chóa đèn là \({y^2} = 27x\) với \(x \le 3\)
Hình ảnh mô phỏng chóa đèn có dạng như hình dưới:
Vẽ các parabol sau:
a) \({y^2} = 16x\)
b) \({y^2} = x\)
c) \({y^2} = 32x\)
Phương pháp giải:
Bước 1: Khởi động phần mềm Geogebra
Bước 2: Nhập phương trình parabol \({y^2} = 2px\) theo cú pháp y^2 = 2px vào vùng nhập lệnh
Bước 3: Quan sát hình vẽ xuất hiện trên vùng làm việc
Lời giải chi tiết:
Thực hiện các bước đã nêu ở phương pháp ta có
a) Nhập phương trình parabol theo cú pháp y^2 = 16x vào vùng nhập lệnh ta được hình parabol dưới đây:
b) Nhập phương trình parabol theo cú pháp y^2 = x vào vùng nhập lệnh ta được hình parabol dưới đây:
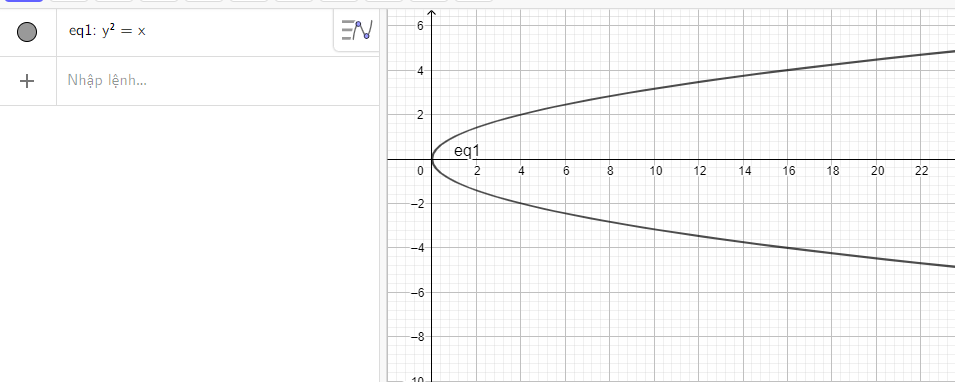
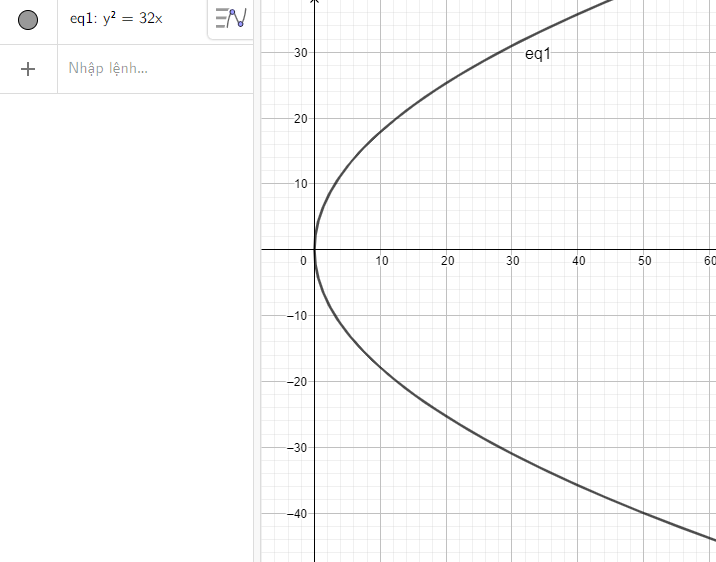
c) Nhập phương trình parabol theo cú pháp y^2 = 32x vào vùng nhập lệnh ta được hình parabol dưới đây:
Hoạt động 3 trang 96 SGK Toán 10 tập 2 - Chân trời sáng tạo yêu cầu học sinh vận dụng kiến thức về vectơ để giải quyết một bài toán thực tế. Bài toán này thường liên quan đến việc xác định vị trí của một điểm trong không gian dựa trên các vectơ chỉ hướng và vectơ gốc.
Để bắt đầu, chúng ta cùng xem lại đề bài của Hoạt động 3:
(Nội dung đề bài cụ thể sẽ được chèn vào đây. Ví dụ: Cho hình vuông ABCD có cạnh bằng a. Gọi M là trung điểm của cạnh BC. Tìm vectơ biểu diễn vectơ AM.)
Để giải bài toán này, chúng ta cần nắm vững các kiến thức sau:
Trong bài toán này, chúng ta sẽ sử dụng phương pháp biểu diễn vectơ thông qua các vectơ thành phần. Cụ thể, chúng ta sẽ phân tích vectơ AM thành tổng của các vectơ AB và BM.
Bước 1: Xác định các vectơ thành phần
Trong hình vuông ABCD, ta có:
Bước 2: Biểu diễn vectơ AM
Ta có thể biểu diễn vectơ AM như sau:
AM = AB + BM
Vì BM = 1/2 BC, ta có:
AM = AB + 1/2 BC
Giả sử hình vuông ABCD có cạnh bằng 2. Khi đó:
Vậy:
AM = (2, 0) + (0, 1) = (2, 1)
Để củng cố kiến thức, bạn có thể tự giải các bài tập tương tự. Dưới đây là một số gợi ý:
Hoạt động 3 trang 96 SGK Toán 10 tập 2 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh hiểu rõ hơn về vectơ và các phép toán vectơ. Hy vọng rằng với hướng dẫn chi tiết này, bạn đã có thể tự tin giải bài tập này và các bài tập tương tự.
Giaitoan.edu.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán. Hãy truy cập website của chúng tôi để tìm kiếm lời giải cho các bài tập khác và nâng cao kiến thức của bạn.