Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 3 trang 84, 85 SGK Toán 10 tập 1 chương trình Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập một cách khoa học và hiệu quả.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, tự tin giải quyết các bài toán Toán 10 và đạt kết quả tốt nhất trong học tập.
Cho hình bình hành ABCD (hình 30), hãy so sánh độ dài và hướng của hai vectơ : Cho D, E, F lần lượt là trung điểm của cạnh BC, CA, AB của tam giác ABC (hình 14).
Cho hình bình hành ABCD (hình 30), hãy so sánh độ dài và hướng của hai vectơ :
a) \(\overrightarrow {AB} \) và \(\overrightarrow {DC} \)
b) \(\overrightarrow {AD} \) và \(\overrightarrow {CB} \)
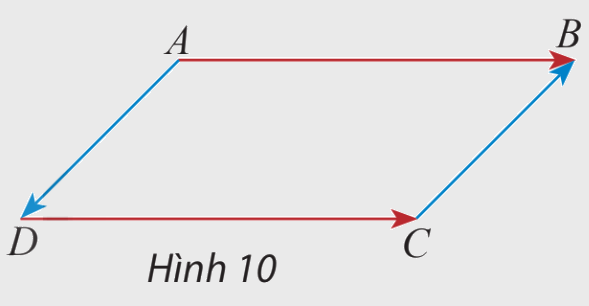
Lời giải chi tiết:
a) Ta có: \(AB = CD \Rightarrow \left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {CD} } \right|\)
\(AB//CD\) và \(\overrightarrow {AB} \), \(\overrightarrow {DC} \) có hướng từ trái sang phải
Suy ra \(\overrightarrow {AB} \) và \(\overrightarrow {DC} \) cùng hướng
b) Ta có: \(AD = CB \Rightarrow \left| {\overrightarrow {AD} } \right| = \left| {\overrightarrow {CB} } \right|\)
\(AD//CB\) và \(\overrightarrow {AD} \)có hướng từ trên xuống dưới, \(\overrightarrow {CB} \) có hướng từ dưới lên trên. Suy ra \(\overrightarrow {AD} \) và \(\overrightarrow {CB} \)ngược hướng
Cho D, E, F lần lượt là trung điểm của cạnh BC, CA, AB của tam giác ABC (hình 14).
a) Tìm các vectơ bằng vectơ \(\overrightarrow {EF} \).
b) Tìm các vectơ đối vectơ \(\overrightarrow {EC} \)
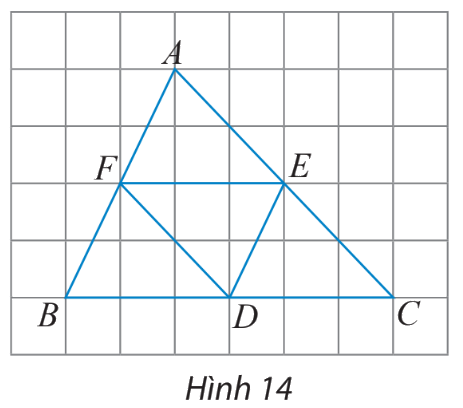
Phương pháp giải:
a)
Bước 1: Từ H14, xác định các đoạn thẳng có độ dài bằng độ dài vectơ \(\overrightarrow {EF} \)
Bước 2: Trong đó liệt kê các vectơ cùng hướng với vectơ \(\overrightarrow {EF} \)
b)
Bước 1: Từ H14, xác định các đoạn thẳng có độ dài bằng độ dài vectơ \(\overrightarrow {EC} \)
Bước 2: Trong đó liệt kê các vectơ ngược hướng với vectơ \(\overrightarrow {EC} \)
Lời giải chi tiết:
Từ giả thiết ta có:
\(AF = FB = ED\); \(AE = EC = FD\); \(BD = DC = EF\)
Từ đó dựa vào hình ta có:
a) Các vectơ bằng vectơ \(\overrightarrow {EF} \)là \(\overrightarrow {DB} \) và \(\overrightarrow {CD} \)
b) Các vectơ đối vectơ \(\overrightarrow {EC} \) là \(\overrightarrow {EA} \) và \(\overrightarrow {DF} \)
Cho hình bình hành ABCD (hình 30), hãy so sánh độ dài và hướng của hai vectơ :
a) \(\overrightarrow {AB} \) và \(\overrightarrow {DC} \)
b) \(\overrightarrow {AD} \) và \(\overrightarrow {CB} \)
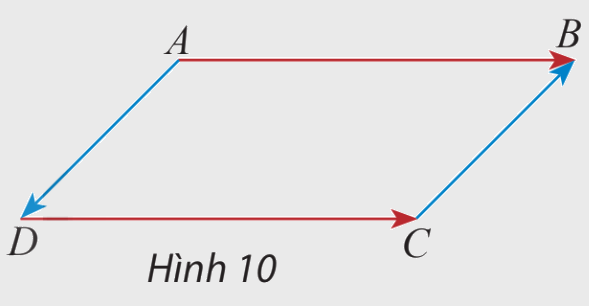
Lời giải chi tiết:
a) Ta có: \(AB = CD \Rightarrow \left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {CD} } \right|\)
\(AB//CD\) và \(\overrightarrow {AB} \), \(\overrightarrow {DC} \) có hướng từ trái sang phải
Suy ra \(\overrightarrow {AB} \) và \(\overrightarrow {DC} \) cùng hướng
b) Ta có: \(AD = CB \Rightarrow \left| {\overrightarrow {AD} } \right| = \left| {\overrightarrow {CB} } \right|\)
\(AD//CB\) và \(\overrightarrow {AD} \)có hướng từ trên xuống dưới, \(\overrightarrow {CB} \) có hướng từ dưới lên trên. Suy ra \(\overrightarrow {AD} \) và \(\overrightarrow {CB} \)ngược hướng
Cho D, E, F lần lượt là trung điểm của cạnh BC, CA, AB của tam giác ABC (hình 14).
a) Tìm các vectơ bằng vectơ \(\overrightarrow {EF} \).
b) Tìm các vectơ đối vectơ \(\overrightarrow {EC} \)
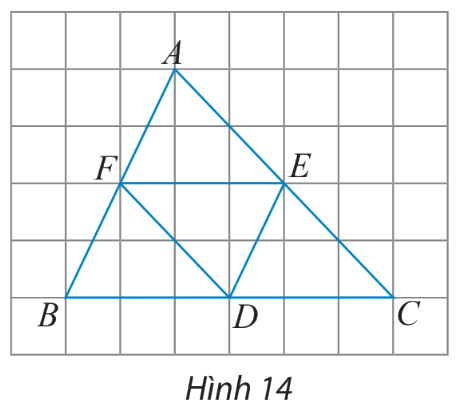
Phương pháp giải:
a)
Bước 1: Từ H14, xác định các đoạn thẳng có độ dài bằng độ dài vectơ \(\overrightarrow {EF} \)
Bước 2: Trong đó liệt kê các vectơ cùng hướng với vectơ \(\overrightarrow {EF} \)
b)
Bước 1: Từ H14, xác định các đoạn thẳng có độ dài bằng độ dài vectơ \(\overrightarrow {EC} \)
Bước 2: Trong đó liệt kê các vectơ ngược hướng với vectơ \(\overrightarrow {EC} \)
Lời giải chi tiết:
Từ giả thiết ta có:
\(AF = FB = ED\); \(AE = EC = FD\); \(BD = DC = EF\)
Từ đó dựa vào hình ta có:
a) Các vectơ bằng vectơ \(\overrightarrow {EF} \)là \(\overrightarrow {DB} \) và \(\overrightarrow {CD} \)
b) Các vectơ đối vectơ \(\overrightarrow {EC} \) là \(\overrightarrow {EA} \) và \(\overrightarrow {DF} \)
Mục 3 trong SGK Toán 10 tập 1 chương trình Chân trời sáng tạo tập trung vào việc ứng dụng kiến thức về vectơ trong hình học. Cụ thể, các em sẽ được làm quen với các khái niệm như tích vô hướng của hai vectơ, góc giữa hai vectơ, và các ứng dụng của tích vô hướng trong việc giải quyết các bài toán liên quan đến khoảng cách, diện tích, và các tính chất hình học khác.
Bài tập mục 3 trang 84, 85 SGK Toán 10 tập 1 Chân trời sáng tạo bao gồm các dạng bài tập khác nhau, từ việc tính tích vô hướng của hai vectơ, tìm góc giữa hai vectơ, đến việc chứng minh các đẳng thức hình học sử dụng tích vô hướng. Để giải quyết các bài tập này một cách hiệu quả, các em cần nắm vững các định nghĩa, tính chất, và công thức liên quan đến tích vô hướng.
Ví dụ: Cho hai vectơ a = (1; 2) và b = (-3; 1). Tính tích vô hướng của hai vectơ này.
Giải: Tích vô hướng của hai vectơ a và b được tính như sau:
a.b = (1)(-3) + (2)(1) = -3 + 2 = -1
Ngoài SGK Toán 10 tập 1 Chân trời sáng tạo, các em có thể tham khảo thêm các tài liệu sau để nâng cao kiến thức và kỹ năng giải bài tập:
Hy vọng với hướng dẫn chi tiết này, các em sẽ tự tin giải quyết các bài tập mục 3 trang 84, 85 SGK Toán 10 tập 1 chương trình Chân trời sáng tạo. Chúc các em học tập tốt và đạt kết quả cao!