Lý thuyết Phương trình quy về phương trình bậc hai - SGK Toán 10 Chân trời sáng tạo

Lý thuyết Phương trình quy về phương trình bậc hai - Toán 10 Chân trời sáng tạo

Chào mừng bạn đến với bài học về lý thuyết Phương trình quy về phương trình bậc hai trong chương trình Toán 10 Chân trời sáng tạo. Bài học này sẽ cung cấp cho bạn những kiến thức nền tảng quan trọng để giải quyết các bài toán liên quan đến phương trình.

Chúng ta sẽ cùng nhau tìm hiểu về các dạng phương trình thường gặp, cách đưa chúng về dạng phương trình bậc hai và các phương pháp giải quyết hiệu quả. Giaitoan.edu.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán.

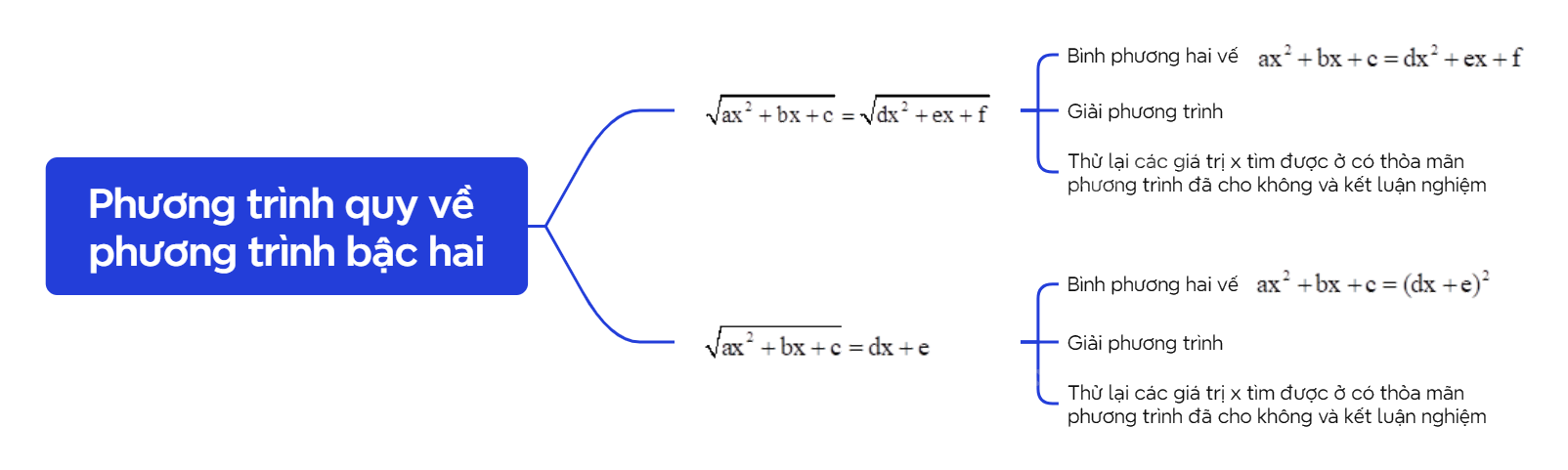
1. Phương trình dạng \(\sqrt {a{x^2} + bx + c} = \sqrt {d{x^2} + ex + f} \)

A. Lý thuyết

1. Phương trình dạng \(\sqrt {a{x^2} + bx + c} = \sqrt {d{x^2} + ex + f} \)

Để giải phương trình \(\sqrt {a{x^2} + bx + c} = \sqrt {d{x^2} + ex + f} \), ta thực hiện như sau:

Bước 1: Bình phương hai vế của phương trình để được phương trình \(a{x^2} + bx + c = d{x^2} + ex + f\).

Bước 2: Giải phương trình vừa nhận được ở B1.

Bước 3: Thử lại các giá trị x tìm được ở B2 có thỏa mãn phương trình đã cho không và kết luận nghiệm.

2. Phương trình dạng \(\sqrt {a{x^2} + bx + c} = dx + e\)

Để giải phương trình \(\sqrt {a{x^2} + bx + c} = dx + e\), ta thực hiện như sau:

Bước 1: Bình phương hai vế của phương trình để được phương trình \(a{x^2} + bx + c = {(dx + e)^2}\).

Bước 2: Giải phương trình vừa nhận được ở B1.

Bước 3: Thử lại các giá trị x tìm được ở B2 có thỏa mãn phương trình đã cho không và kết luận nghiệm.

B. Bài tập

Bài 1: Giải phương trình \(\sqrt {2{x^2} - 4x - 2} = \sqrt {{x^2} - x - 2} \).

Giải:

Bình phương hai vế của phương trình, ta được:

\(2{x^2} - 4 - 2 = {x^2} - x - 2\)

\( \Rightarrow {x^2} - 3x = 0\)

\( \Rightarrow \) x = 0 hoặc x = 3.

Thay lần lượt hai giá trị này của x vào phương trình đã cho, ta chỉ thấy có x = 3 thỏa mãn.

Vậy nghiệm của phương trình đã cho là x = 3.

Bài 2: Giải phương trình \(\sqrt {2{x^2} - 5x - 9} = x - 1\).

Giải:

Bình phương hai vế của phương trình, ta được

\(2{x^2} - 5x - 9 = {(x - 1)^2}\)

\( \Rightarrow 2{x^2} - 5x - 9 = {x^2} - 2x + 1\)

\( \Rightarrow {x^2} - 3x - 10 = 0\)

\( \Rightarrow \) x = -2 hoặc x = 5.

Thay lần lượt hai giá trị này của x vào phương trình đã cho, ta chỉ thấy có x = 5 thỏa mãn.

Vậy nghiệm của phương trình đã cho là x = 5.

Lý thuyết Phương trình quy về phương trình bậc hai - SGK Toán 10 Chân trời sáng tạo 1

Xây dựng nền tảng Toán THPT vững vàng từ hôm nay! Đừng bỏ lỡ Lý thuyết Phương trình quy về phương trình bậc hai - SGK Toán 10 Chân trời sáng tạo đặc sắc thuộc chuyên mục bài tập toán 10 trên nền tảng tài liệu toán. Với bộ bài tập toán thpt được biên soạn chuyên sâu, bám sát chương trình Toán lớp 10, đây chính là "kim chỉ nam" giúp các em tối ưu hóa ôn luyện, củng cố kiến thức cốt lõi và chuẩn bị hành trang vững chắc cho tương lai. Phương pháp học trực quan, logic sẽ mang lại hiệu quả vượt trội trên lộ trình chinh phục đại học!

Lý thuyết Phương trình quy về phương trình bậc hai - SGK Toán 10 Chân trời sáng tạo

Trong chương trình Toán 10 Chân trời sáng tạo, phương trình quy về phương trình bậc hai đóng vai trò quan trọng trong việc rèn luyện kỹ năng giải toán và tư duy logic. Bài viết này sẽ cung cấp một cách đầy đủ và chi tiết về lý thuyết, các dạng bài tập thường gặp và phương pháp giải quyết hiệu quả.

1. Phương trình quy về phương trình bậc hai là gì?

Phương trình quy về phương trình bậc hai là những phương trình có thể được biến đổi về dạng phương trình bậc hai ax² + bx + c = 0 (với a ≠ 0) thông qua một số phép biến đổi đại số.

2. Các dạng phương trình thường gặp

Phương trình chứa căn thức: Các phương trình có chứa căn thức, thường cần phải bình phương hai vế để khử căn thức và đưa về dạng phương trình bậc hai.
Phương trình chứa mẫu thức: Các phương trình có chứa mẫu thức, cần xác định điều kiện xác định của phương trình và quy đồng mẫu thức để giải.
Phương trình tích: Phương trình có dạng P(x) * Q(x) = 0, tương đương với việc giải hai phương trình P(x) = 0 và Q(x) = 0.
Phương trình chia: Phương trình có dạng P(x) / Q(x) = 0, tương đương với việc giải phương trình P(x) = 0 với điều kiện Q(x) ≠ 0.

3. Phương pháp giải phương trình quy về phương trình bậc hai

Biến đổi phương trình: Sử dụng các phép biến đổi đại số (bình phương hai vế, quy đồng mẫu thức, phân tích thành nhân tử,...) để đưa phương trình về dạng ax² + bx + c = 0.
Giải phương trình bậc hai: Sử dụng công thức nghiệm của phương trình bậc hai: x = (-b ± √(b² - 4ac)) / 2a.
Kiểm tra nghiệm: Thay các nghiệm tìm được vào phương trình ban đầu để kiểm tra xem chúng có thỏa mãn điều kiện xác định hay không.

4. Ví dụ minh họa

Ví dụ 1: Giải phương trình √(2x + 1) = x - 1

Giải:

Bình phương hai vế: 2x + 1 = (x - 1)²
Khai triển và rút gọn: 2x + 1 = x² - 2x + 1 => x² - 4x = 0
Phân tích thành nhân tử: x(x - 4) = 0
Giải phương trình: x = 0 hoặc x = 4
Kiểm tra nghiệm:

Với x = 0: √(2*0 + 1) = 1 ≠ 0 - 1 = -1 (loại)
Với x = 4: √(2*4 + 1) = 3 = 4 - 1 (nhận)

Vậy nghiệm của phương trình là x = 4.

Ví dụ 2: Giải phương trình (x + 2) / (x - 1) = 3

Giải:

Điều kiện xác định: x ≠ 1
Quy đồng mẫu thức: x + 2 = 3(x - 1)
Khai triển và rút gọn: x + 2 = 3x - 3 => 2x = 5
Giải phương trình: x = 2.5
Kiểm tra nghiệm: x = 2.5 ≠ 1 (nhận)

Vậy nghiệm của phương trình là x = 2.5.

5. Luyện tập và củng cố kiến thức

Để nắm vững kiến thức về phương trình quy về phương trình bậc hai, bạn nên luyện tập thêm nhiều bài tập khác nhau. Giaitoan.edu.vn cung cấp một hệ thống bài tập phong phú và đa dạng, giúp bạn rèn luyện kỹ năng giải toán một cách hiệu quả.

6. Kết luận

Lý thuyết Phương trình quy về phương trình bậc hai là một phần kiến thức quan trọng trong chương trình Toán 10 Chân trời sáng tạo. Việc nắm vững lý thuyết và phương pháp giải quyết các dạng bài tập khác nhau sẽ giúp bạn tự tin hơn trong các kỳ thi và ứng dụng kiến thức vào thực tế.