Chào mừng bạn đến với bài học về Lý thuyết Hoán vị, chỉnh hợp và tổ hợp - một phần quan trọng trong chương trình SGK Toán 10 Chân trời sáng tạo. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và nâng cao về các khái niệm này, giúp bạn giải quyết các bài toán thực tế một cách hiệu quả.
Tại giaitoan.edu.vn, chúng tôi cam kết mang đến cho bạn trải nghiệm học tập trực tuyến tốt nhất với các bài giảng được trình bày rõ ràng, dễ hiểu và các bài tập đa dạng để bạn luyện tập.
1. Hoán vị a) Định nghĩa
A. Lý thuyết
1. Hoán vị
a) Định nghĩa
| Cho tập hợp A có n phần tử (n ≥ 1). Mỗi cách sắp xếp n phần tử của A theo một thứ tự gọi là một hoán vị các phần tử đó (gọi tắt là hoán vị của A hay của n phần tử). |
b) Số các hoán vị
Kí hiệu \({P_n}\) là số hoán vị của n phần tử. Ta có \({P_n} = n(n - 1)...2.1\). |
Chú ý:
- Ta đưa vào kí hiệu n! = n(n – 1)(n – 2)…2.1 và đọc là n giai thừa hoặc giai thừa của n. Khi đó, \({P_n} = n!\).
- Quy ước: 0! = 1.
2. Chỉnh hợp
a) Định nghĩa
Trong thực tiễn, bên cạnh việc chọn ra một số đối tượng từ những đối tượng cho trước, ta còn cần sắp xếp thứ tự của những đối tượng được chọn ra.
| Cho tập hợp A có n phần tử (n ≥ 1) và số nguyên k với 1 ≤ k ≤ n. Mỗi cách lấy k phần tử của A và sắp xếp chúng theo một thứ tự gọi là một chính hợp chập k của n phần tử đó. |
b) Số các chỉnh hợp
Kí hiệu \(A_n^k\) là số chỉnh hợp chập k của n phần tử \((1 \le k \le n)\). Ta có: \(A_n^k = \frac{{n!}}{{(n - k)!}} = n(n - 1)...(n - k + 1)\). |
Nhận xét: Mỗi hoán vị n phần tử cũng chính là chỉnh hợp chập n của n phần tử đó. Ta có \({P_n} = A_n^n\), \(n \ge 1\).
3. Tổ hợp
a) Định nghĩa
| Cho tập hợp A có n phần tử (n ≥ 1). Mỗi tập con gồm k phần tử (1 ≤ k ≤ n) của A được gọi là một tổ hợp chập k của n phần tử. |
b) Số các tổ hợp
Kí hiệu \(C_n^k\) là số tổ hợp chập k của n phần tử với \(1 \le k \le n\). Ta có: \(C_n^k = \frac{{n!}}{{k!(n - k)!}}\) với \(0 \le k \le n\). |
Chú ý: Người ta quy ước \(C_n^0 = 1\).
Nhận xét:
| Ta có hệ thức \(C_n^k = \frac{{A_n^k}}{{k!}}\). |
4. Tính số các hoán vị, chỉnh hợp, tổ hợp bằng máy tính cầm tay
Với một số máy tính cầm tay, ta có thể tính toán nhanh số các hoán vị, chỉnh hợp và tổ hợp.
Ví dụ 1: Tính \({P_8} = 8!\).

Ta được kết quả 40320.
Ví dụ 2: Tính C\(A_{12}^5\).

Ta được 95040.
Ví dụ 3: Tính \(C_{20}^{11}\).
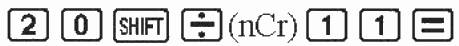
Ta được 167960.
B. Bài tập
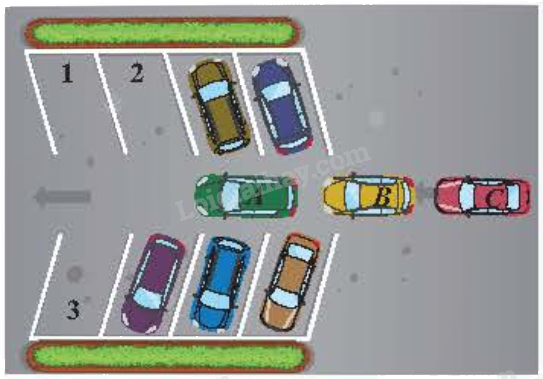
Bài 1: Bài đồ xe ô tô còn lại ba chỗ trống như hình vẽ. Có ba chiếc ô tô (kí hiệu A, B, C) đang đi vào bãi để xe ô tô.
a) Có bao nhiêu cách sắp xếp ba chiếc xe vào ba chỗ trống?
b) Vẽ sơ đồ hình cây về các cách sắp xếp và kiểm tra kết quả tính toán ở trên.
Giải:
a) Mỗi cách sắp xếp ba chiếc xe vào ba chỗ trống là một hoán vị của ba chiếc xe. Do đó, số cách sắp xếp ba chiếc xe vào ba chỗ trống là \({P_3} = 3.2.1 = 6\) (cách).
b) Sơ đồ hình cây như hình dưới. Sơ đồ có ba cành lớn, mỗi cạnh lớn có hai cành vừa, mỗi cành vừa có một cạnh bé. Từ đó, số cạnh bé bằng 3.2.1 = 6. Từ đó, số cách sắp xếp ba chiếc xe vào ba chỗ trống là 6 cách.
Bài 2: Tính số cách xếp thứ tự đã luân lưu 11 m của 5 cầu thủ.
Giải:
Mỗi cách xếp thứ tự đã luận lưu 11 m của 5 cầu thủ là một hoán vị của 5 cầu thủ.
Vậy số cách sắp xếp là: \({P_5} = 5.4.3.2.1 = 120\).
Bài 3: Phần thi chung kết nội dung chạy cự li 1500 m của một giải đấu có 10 vận động viên tham gia. Có bao nhiêu khả năng về kết quả 3 vận động viên đoạt huy chương vàng, bạc và đồng sau khi phần thi kết thúc? Biết rằng không có hai vận động viên nào về đích.
Giải:
Mỗi kết quả về 3 vận động viên đoạt huy chương vàng, bạc và đồng của nội dung thi đấu là một chỉnh hợp chập 3 của 10 vận động viên. Do đó, số kết quả có thể là \(A_{10}^3 = 10.9.8 = 720\).
Bài 4: Ở các căn hộ chung cư, người ta thường dùng các chữ số để tạo mật mã cửa. Gia đình bạn Linh đặt mật mã của là một dãy số gồm 6 chữ số đôi một khác nhau. Hỏi gia đình bạn Linh có bao nhiêu cách để tạo mật mã?
Giải:
Mỗi mật mã của gia đình bạn Linh là một chỉnh hợp chập 6 của 10 chữ số.
Vậy có \(A_{10}^6 = 10.9.8.7.6.5 = 151200\) (cách để tạo mật mã).
Bài 5: Bạn Quân có 4 chiếc áo sơ mi khác màu là áo vàng, áo xanh, áo trắng và áo nâu. Bạn muốn chọn 2 chiếc áo để mặc khi đi du lịch. Viết các tổ hợp chập 2 của 4 chiếc áo.
Giải:
Các tổ hợp chập 2 của 4 chiếc áo là:
{áo vàng; áo xanh}, {áo vàng; áo trắng}, {áo vàng; áo nâu}, {áo xanh; áo trắng}, {áo xanh; áo nâu}, {áo trắng; áo nâu}.
Bài 6: Lớp 10A có 18 bạn nữ và 20 bạn nam.
a) Có bao nhiêu cách chọn 3 bạn nữ trong 18 bạn nữ?
b) Có bao nhiêu cách chọn 5 bạn nam trong 20 bạn nam?
c) Có bao nhiêu cách chọn một tổ xung kích gồm 3 bạn nữ và 5 bạn nam?
Giải:
a) Mỗi cách chọn 3 bạn nữ trong 18 bạn nữ là một tổ hợp chập 3 của 18 phần tử, do đó có \(C_{18}^3\) cách chọn.
b) Mỗi cách chọn 5 bạn nam trong 20 bạn nam là một tổ hợp chập 5 của 20 phần tử, do đó có \(C_{20}^5\) cách chọn.
c) Số cách chọn một tổ xung kích gồm 3 bạn nữ và 5 bạn nam là: \(C_{18}^3.C_{20}^5 = 816.15504 = 12651264\).
Bài 7: Tổ Một có 9 thành viên. Tuần tới là phiên trực nhật của tổ, nên cần phân công 4 bạn đi bề ghế của lớp cho buổi chào cờ. a) Tổ có bao nhiêu cách phân công 4 bạn đi bề ghế? b) Tổ có bao nhiêu cách chọn 5 bạn không phải đi bề ghế?
Giải:
a) Mỗi cách phân công 4 bạn từ 9 bạn là một tổ hợp chập 4 của 9 bạn. Do đó, số cách phân công 4 bạn của tổ đi bề ghế là \(C_9^4 = \frac{{9!}}{{4!5!}} = \frac{{9.8.7.6}}{{4.3.2.1}} = 126\) (cách).
b) Tương tự, số cách chọn 5 bạn từ 9 bạn không phải đi bề ghế là \(C_9^5 = \frac{{9!}}{{5!4!}} = 126\) (cách).
Trong chương trình Toán 10, phần Lý thuyết Hoán vị, chỉnh hợp và tổ hợp đóng vai trò quan trọng trong việc phát triển tư duy logic và kỹ năng giải quyết vấn đề. Đây là nền tảng cho các kiến thức toán học cao hơn, đặc biệt là trong lĩnh vực xác suất thống kê.
Trước khi đi sâu vào từng khái niệm, chúng ta cần hiểu rõ sự khác biệt giữa chúng. Cả ba đều liên quan đến việc sắp xếp và chọn lọc các phần tử từ một tập hợp, nhưng mỗi loại có những quy tắc và ứng dụng riêng.
Hoán vị của n phần tử là số cách sắp xếp n phần tử khác nhau theo một thứ tự nhất định. Ký hiệu là Pn. Công thức tính hoán vị của n phần tử là:
Pn = n!
Ví dụ: Có bao nhiêu cách sắp xếp 3 cuốn sách khác nhau trên một kệ sách?
Giải: P3 = 3! = 3 * 2 * 1 = 6 cách
Chỉnh hợp chập k của n phần tử là số cách sắp xếp k phần tử khác nhau lấy từ n phần tử theo một thứ tự nhất định. Ký hiệu là Ank. Công thức tính chỉnh hợp chập k của n phần tử là:
Ank = n! / (n - k)!
Ví dụ: Có bao nhiêu cách chọn và sắp xếp 2 học sinh từ một lớp 10 học sinh để làm trực nhật?
Giải: A102 = 10! / (10 - 2)! = 10! / 8! = 10 * 9 = 90 cách
Tổ hợp chập k của n phần tử là số cách chọn k phần tử từ n phần tử mà không quan tâm đến thứ tự. Ký hiệu là Cnk. Công thức tính tổ hợp chập k của n phần tử là:
Cnk = n! / (k! * (n - k)!)
Ví dụ: Có bao nhiêu cách chọn 3 học sinh từ một lớp 10 học sinh để tham gia đội văn nghệ?
Giải: C103 = 10! / (3! * 7!) = (10 * 9 * 8) / (3 * 2 * 1) = 120 cách
Các khái niệm này có ứng dụng rộng rãi trong nhiều lĩnh vực của đời sống và khoa học, như:
Để nắm vững kiến thức, bạn nên luyện tập các bài tập sau:
Lý thuyết Hoán vị, chỉnh hợp và tổ hợp là một phần kiến thức quan trọng trong Toán học. Việc hiểu rõ các khái niệm và công thức sẽ giúp bạn giải quyết các bài toán một cách hiệu quả và ứng dụng vào thực tế. Hãy luyện tập thường xuyên để củng cố kiến thức và nâng cao kỹ năng giải quyết vấn đề.