Bài 17 trang 75 SGK Toán 10 tập 2 thuộc chương trình Toán 10 Chân trời sáng tạo, yêu cầu học sinh vận dụng kiến thức về vectơ để giải quyết các bài toán liên quan đến hình học. Bài tập này thường gặp trong các kỳ kiểm tra và thi cử, do đó việc nắm vững phương pháp giải là vô cùng quan trọng.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 17 trang 75 SGK Toán 10 tập 2, giúp các em học sinh hiểu rõ bản chất của bài toán và tự tin giải các bài tập tương tự.
Cổng trời của một thành phố dạng hình parabol có khoảng cách giữa hai chân cổng là 192 m (hình 3). Từ một điểm M trên thân cổng, người ta đo được khoảng cách đến mặt đất là 2 m và khoảng cách từ chân đường vuông góc kẻ từ M xuống mặt đất đến chân cổng gần nhất là 0,5 m. Tính chiều cao của cổng
Đề bài
Cổng trời của một thành phố dạng hình parabol có khoảng cách giữa hai chân cổng là 192 m (hình 3). Từ một điểm M trên thân cổng, người ta đo được khoảng cách đến mặt đất là 2 m và khoảng cách từ chân đường vuông góc kẻ từ M xuống mặt đất đến chân cổng gần nhất là 0,5 m. Tính chiều cao của cổng
Phương pháp giải - Xem chi tiết
Bước 1: Gắn hệ trục tọa độ Oxy
Bước 2: Gọi phương trình chính tắc mô phỏng cổng là \({y^2} = 2px\)
Bước 3: Thay điểm M vào phương trình, xác định phương trình parabol
Bước 4: Xác định chiều cao của cổng
Lời giải chi tiết
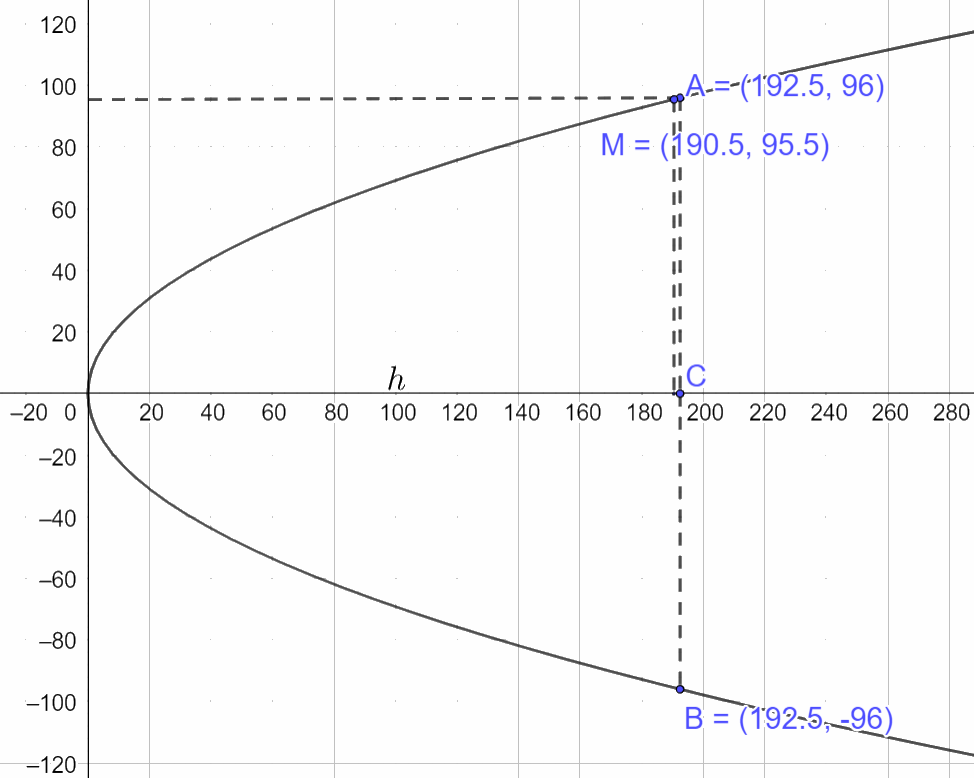
Gắn hệ trục Oxy vào chiếc cổng, gọi chiều cao của cổng là h ta vẽ lại parabol như dưới đây:
Phương trình parabol mô phỏng cổng có dạng \({y^2} = 2px\)
Theo giả thiết \(AB = 2{y_A} = 192 \Rightarrow {y_A} = 96,OC = h \Rightarrow M\left( {h - 2;95,5} \right),A\left( {h;96} \right)\)
Thay tọa độ các điểm \(M\left( {h - 2;95,5} \right),A\left( {h;96} \right)\) vào phương trình \({y^2} = 2px\) ta có:
\(\left\{ \begin{array}{l}95,{5^2} = 2p\left( {h - 2} \right)\\{96^2} = 2ph\end{array} \right. \Rightarrow \left\{ \begin{array}{l}p = \frac{{383}}{{16}}\\h \simeq 192,5\end{array} \right.\)
Vậy chiều cao của cổng gần bằng 192,5 m
Bài 17 trang 75 SGK Toán 10 tập 2 – Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về vectơ và ứng dụng vào giải quyết các bài toán hình học. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các khái niệm cơ bản về vectơ, các phép toán vectơ và các tính chất liên quan.
Bài 17 yêu cầu học sinh thực hiện các thao tác với vectơ, chẳng hạn như tìm tọa độ của vectơ, tính độ dài của vectơ, kiểm tra xem hai vectơ có cùng phương hay không, và giải các bài toán liên quan đến hình học sử dụng vectơ.
Để giải bài 17 trang 75 SGK Toán 10 tập 2, chúng ta có thể áp dụng các phương pháp sau:
Bài 17.1: Cho A(1; 2), B(3; 4). Tìm tọa độ của vectơ AB.
Giải:
Vectơ AB được tính bằng hiệu tọa độ của điểm B trừ đi tọa độ của điểm A:
AB = (3 - 1; 4 - 2) = (2; 2)
Vậy tọa độ của vectơ AB là (2; 2).
Bài 17.2: Cho vectơ a = (1; -2) và b = (3; 1). Tính tích vô hướng của a và b.
Giải:
Tích vô hướng của hai vectơ a và b được tính bằng tổng tích các hoành độ và tung độ tương ứng:
a.b = (1 * 3) + (-2 * 1) = 3 - 2 = 1
Vậy tích vô hướng của a và b là 1.
Bài 17.3: Cho A(2; 1), B(4; 3), C(6; 2). Chứng minh rằng A, B, C thẳng hàng.
Giải:
Để chứng minh A, B, C thẳng hàng, ta cần chứng minh vectơ AB và AC cùng phương. Tức là tồn tại một số k sao cho AC = kAB.
AB = (4 - 2; 3 - 1) = (2; 2)
AC = (6 - 2; 2 - 1) = (4; 1)
Ta thấy không tồn tại số k nào thỏa mãn AC = kAB. Do đó, A, B, C không thẳng hàng.
Vectơ là một công cụ mạnh mẽ trong hình học, giúp chúng ta giải quyết nhiều bài toán phức tạp một cách dễ dàng. Vectơ được sử dụng để:
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải bài 17 trang 75 SGK Toán 10 tập 2 – Chân trời sáng tạo và đạt kết quả tốt trong môn Toán.