Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 1 trang 64, 65 SGK Toán 10 tập 2 chương trình Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập một cách khoa học.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, tự tin giải quyết các bài toán Toán 10 và đạt kết quả tốt nhất trong học tập.
Viết phương trình chính tắc của elip trong hình 4 Một đường hầm có mặt các hình nửa Elip cao 4 m, rộng 10 m (hình 5). Viết phương trình chính tắc của elip đó.
Một đường hầm có mặt các hình nửa Elip cao 4 m, rộng 10 m (hình 5). Viết phương trình chính tắc của elip đó.
Phương pháp giải:
Phương trình chính tắc của elip có dạng \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)
Lời giải chi tiết:
Chiều cao là 4 m tương ứng với \(b = 4\)
Chiều rộng bằng 10 m nên \(2a = 10 \Rightarrow a = 5\)
Vậy phương trình chính tắc của elip có dạng \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{16} = 1\)
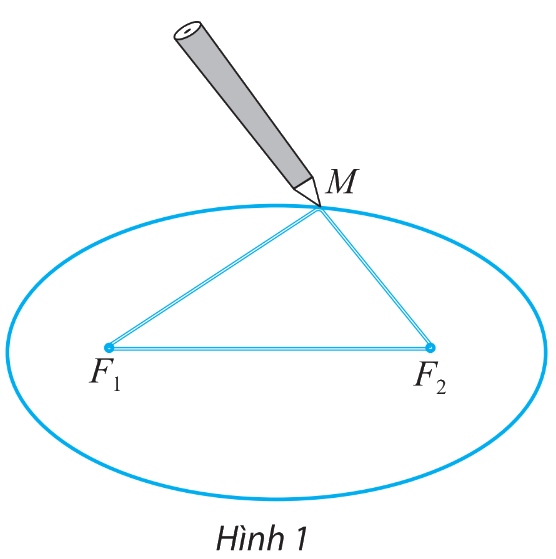
Lấy một tấm bìa, ghim hai cái đinh lên đó tại hai điểm \({F_1}\) và \({F_2}\). Lấy một vòng dây kín không đàn hồi có độ dài lớn hơn hai lần đoạn \({F_1}{F_2}\). Quàng vòng dây đó qua hai chiếc đinh và kéo căng tại một điểm M nào đó. Tựa đầu bút chì vào trong vòng dây tại điểm M rồi di chuyển sao cho dây luôn luôn căng. Đầu bút chì vạch lên tấm bìa một đường mà người ta gọi là đường elip.
Cho biết 2c là khoảng cách \({F_1}{F_2}\) và \(2a + 2c\) là độ dài của vòng dây.
Tính tổng hai khoảng cách \({F_1}M\) và \({F_2}M\)
Lời giải chi tiết:
Ta có chiều dài vòng dây là:
\(M{F_1} + {F_1}{F_2} + {F_2}M = 2a + 2c \Rightarrow M{F_1} + {F_2}M = 2a + 2c - {F_1}{F_2} = 2a\)
Vậy tổng khoảng cách \({F_1}M\) và \({F_2}M\) là 2a
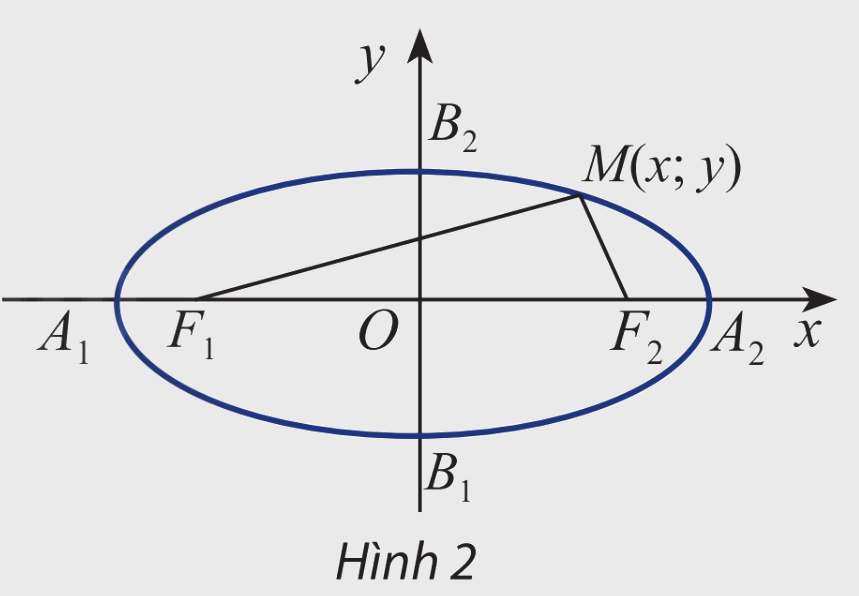
Cho elip (E) có các tiêu điểm \({F_1}\) và \({F_2}\) và đặt \({F_1}{F_2} = 2c\). Chọn hệ trục tọa độ Oxy sao cho \({F_1}( - c;0)\) và \({F_2}(c;0)\)
Xét điểm \(M(x;y)\)
a) Tính \({F_1}M\) và \({F_2}M\) theo x, y và c
b) Giải thích phát biểu sau:
\(M(x;y) \in (E) \Leftrightarrow \sqrt {{{\left( {x + c} \right)}^2} + {y^2}} + \sqrt {{{\left( {x - c} \right)}^2} + {y^2}} = 2a\)
Phương pháp giải:
Sử dụng phương pháp tọa độ trong mặt phẳng
Lời giải chi tiết:
a) Ta có:
\(\overrightarrow {{F_1}M} = \left( {x + c;y} \right) \Rightarrow {F_1}M = \sqrt {{{\left( {x + c} \right)}^2} + {y^2}} \)
\(\overrightarrow {{F_2}M} = \left( {x - c;y} \right) \Rightarrow {F_2}M = \sqrt {{{\left( {x - c} \right)}^2} + {y^2}} \)
b) Ta có \(M(x;y) \in (E)\) nên \({F_1}M + {F_2}M = 2a \Leftrightarrow \sqrt {{{\left( {x + c} \right)}^2} + {y^2}} + \sqrt {{{\left( {x - c} \right)}^2} + {y^2}} = 2a\)
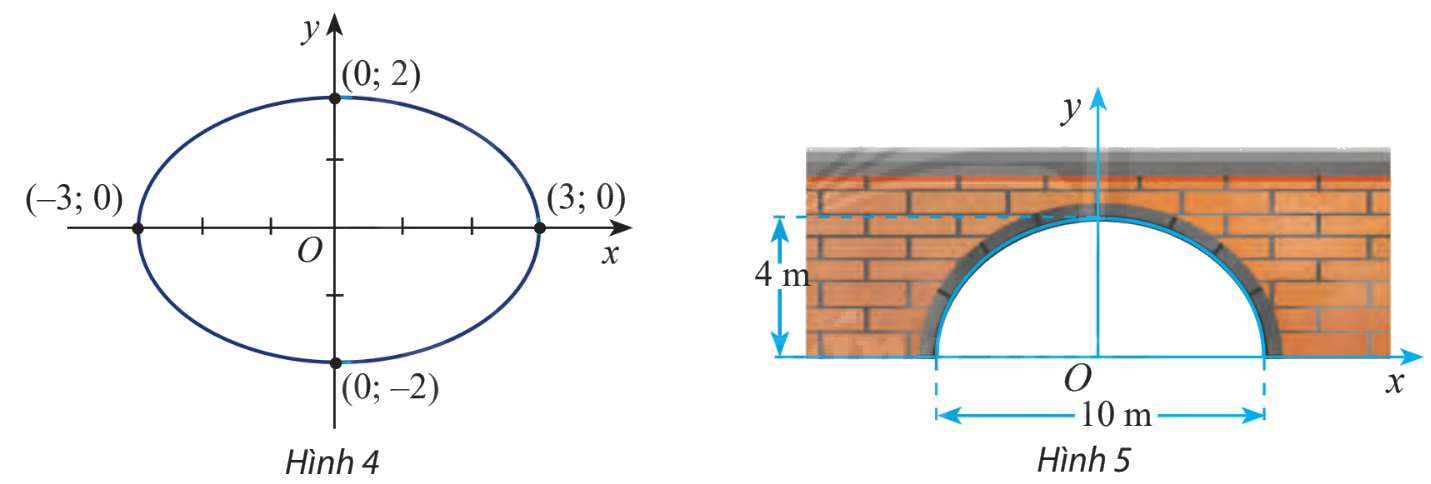
Viết phương trình chính tắc của elip trong hình 4
Phương pháp giải:
Phương trình chính tắc của elip có dạng \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) với \(M(x;y) \in (E);b = \sqrt {{a^2} - {c^2}} \)
Lời giải chi tiết:
Dựa vào hình vẽ ta thấy \(a = 3,c = 2 \Rightarrow b = \sqrt {{a^2} - {c^2}} = \sqrt {{3^2} - {2^2}} = \sqrt 5 \)
Vậy phương trình chính tắc của elip có dạng \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{5} = 1\)
Lời giải chi tiết:
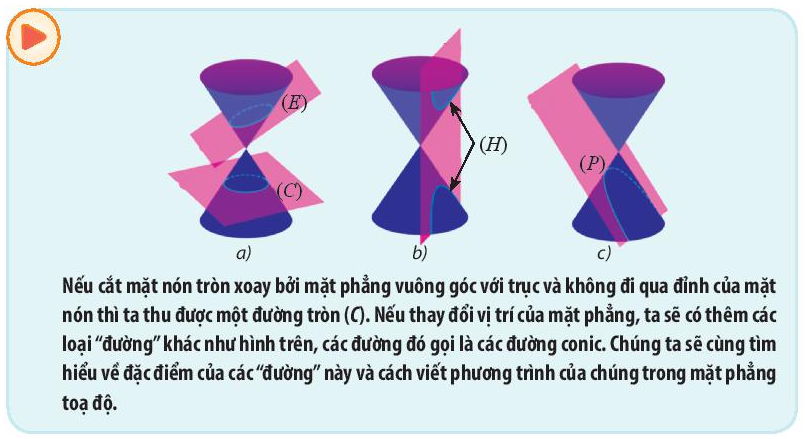
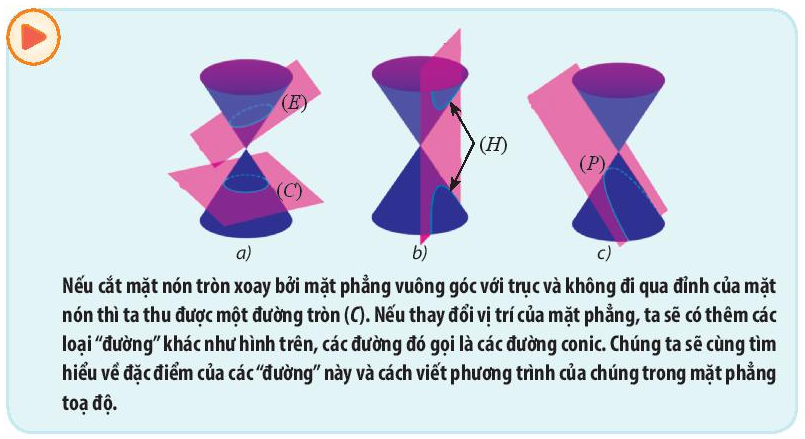
Qua bài học ta thấy rằng hình dạng của các đường là phương trình chính tắc của chúng như sau:
(E) có tên gọi là elip, phương trình: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)
(H) có tên gọi là hypebol, phương trình: \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\)
(P) có tên gọi là parabol, phương trình: \({y^2} = 2px\)
Lời giải chi tiết:
Qua bài học ta thấy rằng hình dạng của các đường là phương trình chính tắc của chúng như sau:
(E) có tên gọi là elip, phương trình: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)
(H) có tên gọi là hypebol, phương trình: \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\)
(P) có tên gọi là parabol, phương trình: \({y^2} = 2px\)
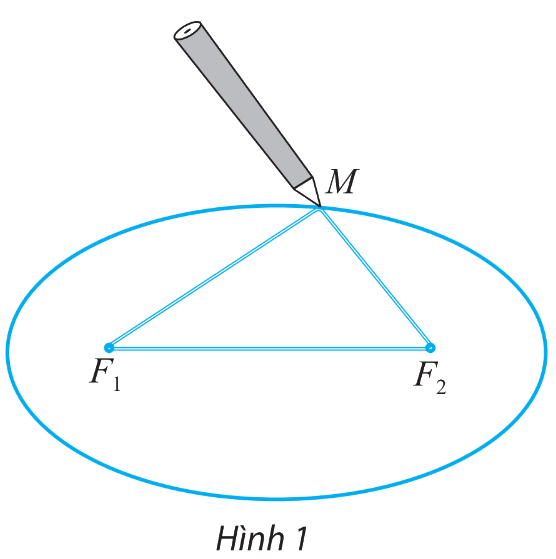
Lấy một tấm bìa, ghim hai cái đinh lên đó tại hai điểm \({F_1}\) và \({F_2}\). Lấy một vòng dây kín không đàn hồi có độ dài lớn hơn hai lần đoạn \({F_1}{F_2}\). Quàng vòng dây đó qua hai chiếc đinh và kéo căng tại một điểm M nào đó. Tựa đầu bút chì vào trong vòng dây tại điểm M rồi di chuyển sao cho dây luôn luôn căng. Đầu bút chì vạch lên tấm bìa một đường mà người ta gọi là đường elip.
Cho biết 2c là khoảng cách \({F_1}{F_2}\) và \(2a + 2c\) là độ dài của vòng dây.
Tính tổng hai khoảng cách \({F_1}M\) và \({F_2}M\)
Lời giải chi tiết:
Ta có chiều dài vòng dây là:
\(M{F_1} + {F_1}{F_2} + {F_2}M = 2a + 2c \Rightarrow M{F_1} + {F_2}M = 2a + 2c - {F_1}{F_2} = 2a\)
Vậy tổng khoảng cách \({F_1}M\) và \({F_2}M\) là 2a
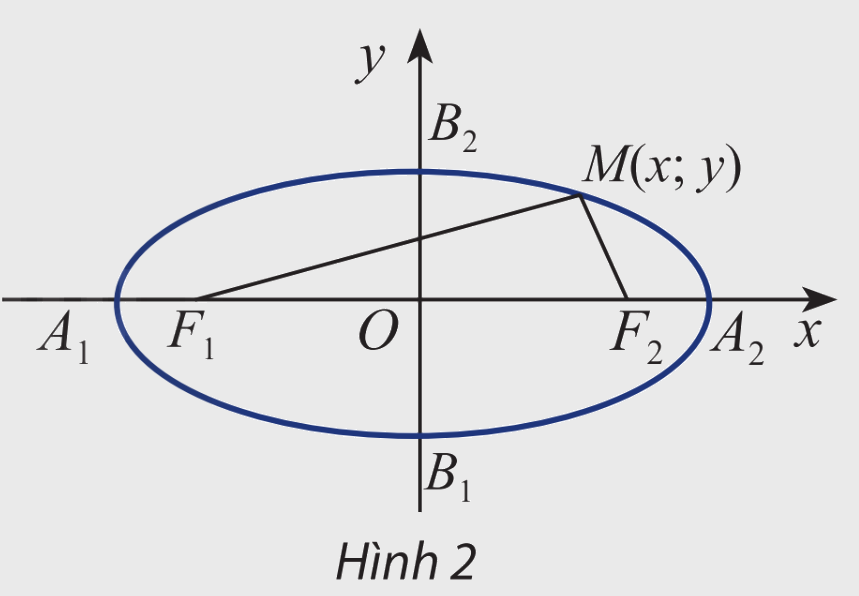
Cho elip (E) có các tiêu điểm \({F_1}\) và \({F_2}\) và đặt \({F_1}{F_2} = 2c\). Chọn hệ trục tọa độ Oxy sao cho \({F_1}( - c;0)\) và \({F_2}(c;0)\)
Xét điểm \(M(x;y)\)
a) Tính \({F_1}M\) và \({F_2}M\) theo x, y và c
b) Giải thích phát biểu sau:
\(M(x;y) \in (E) \Leftrightarrow \sqrt {{{\left( {x + c} \right)}^2} + {y^2}} + \sqrt {{{\left( {x - c} \right)}^2} + {y^2}} = 2a\)
Phương pháp giải:
Sử dụng phương pháp tọa độ trong mặt phẳng
Lời giải chi tiết:
a) Ta có:
\(\overrightarrow {{F_1}M} = \left( {x + c;y} \right) \Rightarrow {F_1}M = \sqrt {{{\left( {x + c} \right)}^2} + {y^2}} \)
\(\overrightarrow {{F_2}M} = \left( {x - c;y} \right) \Rightarrow {F_2}M = \sqrt {{{\left( {x - c} \right)}^2} + {y^2}} \)
b) Ta có \(M(x;y) \in (E)\) nên \({F_1}M + {F_2}M = 2a \Leftrightarrow \sqrt {{{\left( {x + c} \right)}^2} + {y^2}} + \sqrt {{{\left( {x - c} \right)}^2} + {y^2}} = 2a\)
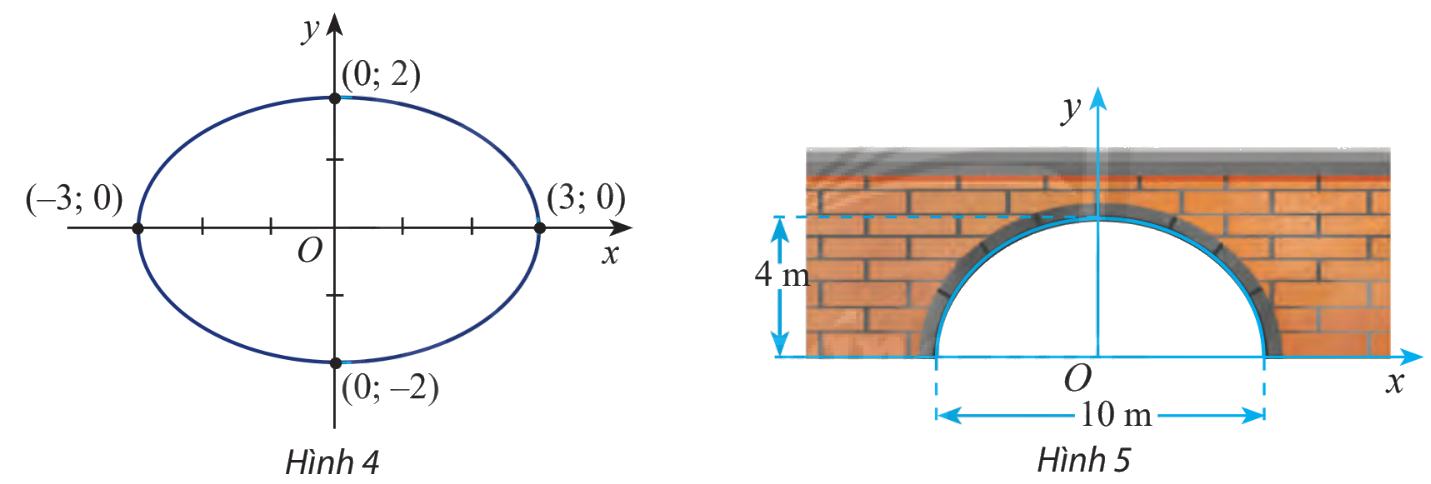
Viết phương trình chính tắc của elip trong hình 4
Phương pháp giải:
Phương trình chính tắc của elip có dạng \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) với \(M(x;y) \in (E);b = \sqrt {{a^2} - {c^2}} \)
Lời giải chi tiết:
Dựa vào hình vẽ ta thấy \(a = 3,c = 2 \Rightarrow b = \sqrt {{a^2} - {c^2}} = \sqrt {{3^2} - {2^2}} = \sqrt 5 \)
Vậy phương trình chính tắc của elip có dạng \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{5} = 1\)
Một đường hầm có mặt các hình nửa Elip cao 4 m, rộng 10 m (hình 5). Viết phương trình chính tắc của elip đó.
Phương pháp giải:
Phương trình chính tắc của elip có dạng \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)
Lời giải chi tiết:
Chiều cao là 4 m tương ứng với \(b = 4\)
Chiều rộng bằng 10 m nên \(2a = 10 \Rightarrow a = 5\)
Vậy phương trình chính tắc của elip có dạng \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{16} = 1\)
Mục 1 của chương trình Toán 10 tập 2 Chân trời sáng tạo thường tập trung vào các khái niệm và ứng dụng của đường thẳng trong mặt phẳng tọa độ. Các bài tập trong mục này thường yêu cầu học sinh vận dụng kiến thức về phương trình đường thẳng, hệ số góc, khoảng cách giữa hai điểm, và các tính chất hình học liên quan.
Để tìm phương trình đường thẳng, ta cần xác định đủ các yếu tố cần thiết, ví dụ như hai điểm thuộc đường thẳng, một điểm và hệ số góc, hoặc một điểm và đường thẳng song song/vuông góc với nó. Sau đó, ta có thể sử dụng các công thức và phương pháp đã học để tìm phương trình đường thẳng.
Ví dụ: Cho hai điểm A(1; 2) và B(3; 4). Tìm phương trình đường thẳng AB.
Để tính khoảng cách giữa hai điểm A(xA; yA) và B(xB; yB), ta sử dụng công thức:
AB = √((xB - xA)2 + (yB - yA)2)
Ví dụ: Tính khoảng cách giữa hai điểm C(0; 0) và D(3; 4).
CD = √((3 - 0)2 + (4 - 0)2) = √(9 + 16) = √25 = 5
Để tìm giao điểm của hai đường thẳng, ta giải hệ phương trình gồm phương trình của hai đường thẳng. Nghiệm của hệ phương trình chính là tọa độ giao điểm của hai đường thẳng.
Ví dụ: Tìm giao điểm của hai đường thẳng d1: y = x + 1 và d2: y = -x + 3.
Giải hệ phương trình:
{ y = x + 1y = -x + 3 }
=> x + 1 = -x + 3 => 2x = 2 => x = 1
=> y = 1 + 1 = 2
Vậy giao điểm của hai đường thẳng là (1; 2).
Hy vọng với hướng dẫn chi tiết này, các em học sinh đã có thể tự tin giải các bài tập mục 1 trang 64, 65 SGK Toán 10 tập 2 Chân trời sáng tạo. Chúc các em học tập tốt và đạt kết quả cao!