Chào mừng bạn đến với bài học về lý thuyết Giá trị lượng giác của một góc từ 0 đến 180 độ, thuộc chương trình SGK Toán 10 - CTST. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về các giá trị lượng giác của các góc trong khoảng từ 0 đến 180 độ.
Chúng ta sẽ cùng nhau tìm hiểu định nghĩa, tính chất và các công thức liên quan đến sin, cosin, tang và cotang của một góc. Đồng thời, bài học cũng sẽ giúp bạn nắm vững cách áp dụng lý thuyết vào giải các bài tập thực tế.
1. GIÁ TRỊ LƯỢNG GIÁC 2. QUAN HỆ GIỮA CÁC GIÁ TRỊ LƯỢNG GIÁC CỦA HAI GÓC BÙ NHAU 3. CÁC GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT SỐ GÓC ĐẶC BIỆT
1. GIÁ TRỊ LƯỢNG GIÁC
+) Với mỗi góc \(\alpha ({0^o} \le \alpha \le {180^o})\) có duy nhất điểm \(M({x_0};{y_0})\) trên nửa đường tròn đơn vị để \(\widehat {xOM} = \alpha .\)Khi đó:
\(\sin \alpha = {y_0}\) là tung độ của M
\(\cos \alpha = {x_0}\) là hoành độ của M
\(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{{{y_0}}}{{{x_0}}}(\alpha \ne {90^o})\)
\(\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{{{x_0}}}{{{y_0}}}(\alpha \ne {0^o},\alpha \ne {180^o})\)
2. QUAN HỆ GIỮA CÁC GIÁ TRỊ LƯỢNG GIÁC CỦA HAI GÓC BÙ NHAU
Hai góc bù nhau, \(\alpha \) và \({180^o} - \alpha \):
\(\begin{array}{l}\sin \left( {{{180}^o} - \alpha } \right) = \sin \alpha \\\cos \left( {{{180}^o} - \alpha } \right) = - \cos \alpha \\\tan \left( {{{180}^o} - \alpha } \right) = - \tan \alpha (\alpha \ne {90^o})\\\cot \left( {{{180}^o} - \alpha } \right) = - \cot \alpha ({0^o} < \alpha < {180^o})\end{array}\)
Hai góc phụ nhau, \(\alpha \) và \({90^o} - \alpha \):
\(\begin{array}{l}\sin \left( {{{90}^o} - \alpha } \right) = \cos \alpha \\\cos \left( {{{90}^o} - \alpha } \right) = \sin \alpha \\\tan \left( {{{90}^o} - \alpha } \right) = \cot \alpha (\alpha \ne {90^o},{0^o} < \alpha < {180^o})\\\cot \left( {{{90}^o} - \alpha } \right) = \tan \alpha (\alpha \ne {90^o},{0^o} < \alpha < {180^o})\end{array}\)
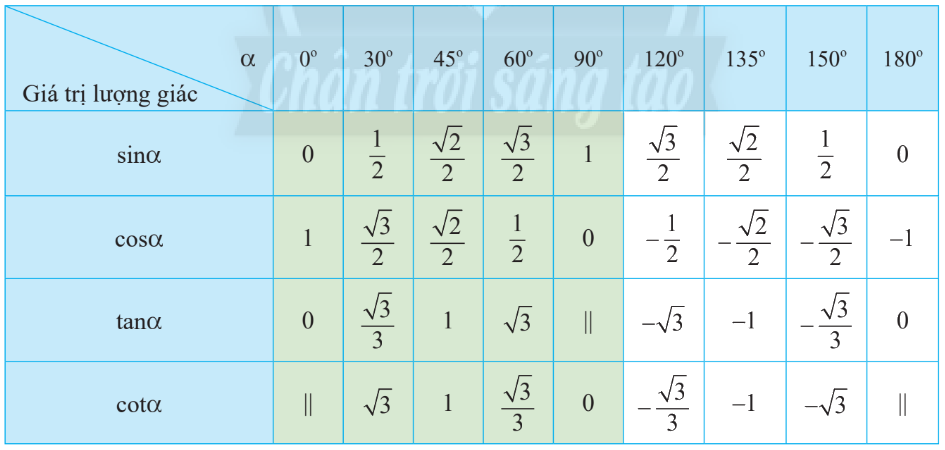
3. CÁC GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT SỐ GÓC ĐẶC BIỆT
4. SỬ DỤNG MÁY TÍNH CẦM TAY ĐỂ TÍNH CÁC GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC
a) Tính các giá trị lượng giác của góc
Bước 1: Cài đặt đơn vị đo góc (độ hoặc radian)
Bước 2: Vào chế độ tính toán
Chú ý: Để tính \(\cot \alpha \) ta tính \(\frac{1}{{\tan \alpha }}\).
b) Xác định số đo của góc khi biết giá trị lượng giác của góc đó
Để tìm \(\alpha \) khi biết \(\cot \alpha \) ta tính \(\tan \alpha = \frac{1}{{\cot \alpha }}\) rồi tính \(\alpha \) sau.
Trong chương trình Toán 10 - CTST, phần Giá trị lượng giác của một góc từ 0 đến 180 độ đóng vai trò nền tảng cho việc học tập các kiến thức lượng giác nâng cao hơn. Bài viết này sẽ trình bày chi tiết lý thuyết, ví dụ minh họa và các bài tập ứng dụng để giúp bạn hiểu rõ và nắm vững kiến thức này.
Cho góc α (0° ≤ α ≤ 180°). Xét đường tròn lượng giác đơn vị (bán kính bằng 1) với tâm O. Gọi M là điểm trên đường tròn sao cho góc xOM bằng α. Tọa độ của điểm M là (x0; y0).
| Góc α | sin α | cos α | tan α | cot α |
|---|---|---|---|---|
| 0° | 0 | 1 | 0 | Không xác định |
| 30° | 1/2 | √3/2 | √3/3 | √3 |
| 45° | √2/2 | √2/2 | 1 | 1 |
| 60° | √3/2 | 1/2 | √3 | √3/3 |
| 90° | 1 | 0 | Không xác định | 0 |
| 180° | 0 | -1 | 0 | Không xác định |
Dấu của các giá trị lượng giác phụ thuộc vào góc α nằm trong góc phần tư nào của đường tròn lượng giác:
Bài 1: Tính giá trị của sin 120° và cos 150°.
Giải:
Bài 2: Cho α là góc nhọn. Biết sin α = 3/5. Tính cos α và tan α.
Giải:
Lý thuyết Giá trị lượng giác của một góc từ 0 đến 180 độ là kiến thức cơ bản và quan trọng trong chương trình Toán 10 - CTST. Việc nắm vững lý thuyết và các công thức liên quan sẽ giúp bạn giải quyết các bài toán lượng giác một cách hiệu quả và chính xác. Hãy luyện tập thường xuyên để củng cố kiến thức và nâng cao kỹ năng giải toán của mình.