Bài 3 trang 102 SGK Toán 10 tập 1 – Chân trời sáng tạo là một bài tập quan trọng trong chương trình học Toán 10. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng của vectơ trong hình học để giải quyết các bài toán cụ thể.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 3 trang 102 SGK Toán 10 tập 1 – Chân trời sáng tạo, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho hình thoi ABCD đi có cạnh bằng a và có góc A bằng 60. Tìm độ dài của các vectơ sau:
Đề bài
Cho hình thoi ABCD đi có cạnh bằng a và có góc A bằng \(60^\circ \). Tìm độ dài của các vectơ sau: \(\overrightarrow p = \overrightarrow {AB} + \overrightarrow {AD} ;\overrightarrow u = \overrightarrow {AB} - \overrightarrow {AD} ;\overrightarrow v = 2\overrightarrow {AB} - \overrightarrow {AC} \).
Phương pháp giải - Xem chi tiết
Quy tắc ba điểm \(\overrightarrow {AB} = \overrightarrow {AO} + \overrightarrow {OB} \)
Quy tắc hình bình hành \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \) (với ABCD là hình bình hành);
Quy tắc hiệu: \(\overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow {CB} \)
Áp dụng các quy tắc trên để xác định vecto \(\overrightarrow p ,\overrightarrow u ,\overrightarrow v \) rồi tính độ dài.
Lời giải chi tiết
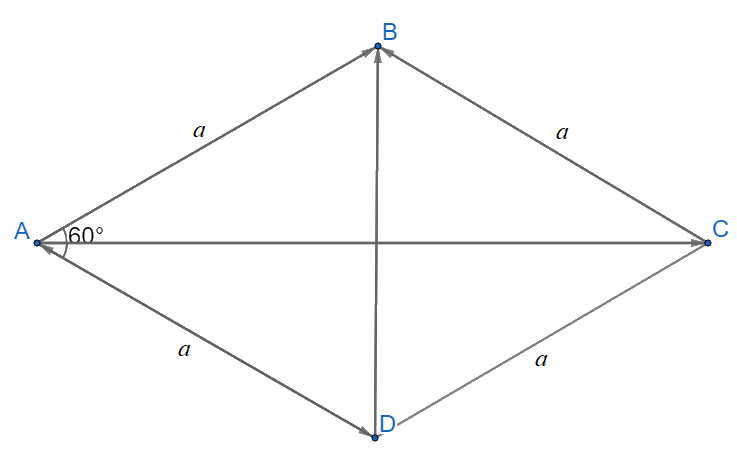
+) ABCD là hình thoi nên cũng là hình bình hành
Áp dụng quy tắc hình bình hành ta có:
\(\overrightarrow p = \overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
\(\Rightarrow |\overrightarrow p| = | \overrightarrow {AC}| =AC \)
+) \(\overrightarrow u = \overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {DB} \)
\(\Rightarrow |\overrightarrow u| = | \overrightarrow {DB}| =DB\)
+) \(\overrightarrow v = 2\overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow {AB} + \left( {\overrightarrow {AB} - \overrightarrow {AC} } \right) = \overrightarrow {AB} + \overrightarrow {CB} \)\( = \overrightarrow {AB} + \overrightarrow {DA} = \overrightarrow {DB} \)
\(\Rightarrow |\overrightarrow v| = | \overrightarrow {DB}| =DB\)
+ Tính \(AC, DB\)
Tam giác ABD có \(AB=AD=a, \widehat A = 60^o\) nên nó là tam giác đều. Do đó DB = a.
Gọi O là giao điểm hai đường chéo.
Ta có: \(AO = AB. \sin B = a. \sin 60^o = \frac {a \sqrt 3}{2} \Rightarrow AC = a \sqrt 3\)
Vậy \(|\overrightarrow p| = a \sqrt 3 ,|\overrightarrow u| = a, |\overrightarrow v| = a.\)
Bài 3 trang 102 SGK Toán 10 tập 1 – Chân trời sáng tạo thuộc chương trình học về vectơ trong không gian. Để giải bài tập này, học sinh cần nắm vững các khái niệm cơ bản về vectơ, bao gồm:
Dưới đây là đề bài và lời giải chi tiết bài 3 trang 102 SGK Toán 10 tập 1 – Chân trời sáng tạo:
Cho hình vuông ABCD có cạnh bằng a. Gọi M là trung điểm của cạnh BC. Tính độ dài của vectơ AM.
Để tính độ dài của vectơ AM, ta có thể sử dụng định lý Pitago trong tam giác vuông ABM. Ta có:
AB = a (độ dài cạnh hình vuông)
BM = a/2 (M là trung điểm của BC)
Áp dụng định lý Pitago trong tam giác vuông ABM, ta có:
AM2 = AB2 + BM2 = a2 + (a/2)2 = a2 + a2/4 = 5a2/4
Suy ra: AM = √(5a2/4) = (a√5)/2
Vậy, độ dài của vectơ AM là (a√5)/2.
Bài tập này không chỉ giúp học sinh củng cố kiến thức về vectơ mà còn rèn luyện kỹ năng giải toán hình học. Để giải bài tập này một cách hiệu quả, học sinh cần:
Ngoài ra, học sinh có thể tự đặt ra các bài tập tương tự để luyện tập và nâng cao kỹ năng giải toán. Ví dụ, thay đổi vị trí của điểm M trên cạnh BC hoặc thay đổi hình dạng của hình ABCD thành các hình khác như hình chữ nhật, hình thoi,...
Để hiểu rõ hơn về ứng dụng của vectơ trong hình học, học sinh có thể tham khảo các bài tập tương tự sau:
Bài 3 trang 102 SGK Toán 10 tập 1 – Chân trời sáng tạo là một bài tập quan trọng giúp học sinh nắm vững kiến thức về vectơ và ứng dụng của vectơ trong hình học. Hy vọng với lời giải chi tiết và phân tích trên, các em học sinh sẽ tự tin giải bài tập này và các bài tập tương tự.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Chúc các em học tập tốt!