Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 tập 2 của giaitoan.edu.vn. Ở đây, chúng tôi cung cấp lời giải chi tiết và dễ hiểu cho tất cả các bài tập trong sách giáo khoa Toán 10 tập 2, chương trình Chân trời sáng tạo.
Mục 3 trang 54, 55, 56, 57 tập trung vào các kiến thức quan trọng về... (nội dung cụ thể của mục 3 sẽ được điền vào đây khi có thông tin chi tiết)
Cho hai đường thẳng xy và zt cắt nhau tại O và cho biết xOz=38 (hình 6) Tìm số đo của góc giữa hai đường thẳng trong các trường hợp sau Tìm số đo của góc giữa hai đường thẳng là đồ thị của hai hàm số y = x và y = 2x + 1
Cho hai đường thẳng
\({\Delta _1}:{a_1}x + {b_1}y + {c_1} = 0\) (\({a_1}^2 + {b_1}^2 > 0\)) và \({\Delta _2}:{a_2}x + {b_2}y + {c_2} = 0\) \(\left( {{a_2}^2 + {b_2}^2 > 0} \right)\)
có vectơ pháp tuyến lần lượt là \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \).
Tìm tọa độ \(\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} \) và tính \(\cos \left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right)\).
Phương pháp giải:
+) Tọa độ của \(\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} \) được xác định từ phương trình tổng quát của hai đường thẳng.
+) Áp dụng biểu thức tọa độ của vectơ trong mặt phẳng.
Lời giải chi tiết:
+) Từ phương trình \({\Delta _1}:{a_1}x + {b_1}y + {c_1} = 0\) ta xác định được tọa độ của vectơ \(\overrightarrow {{n_1}} \) là \(\left( {{a_1};{b_1}} \right)\).
+) Từ phương trình \({\Delta _2}:{a_2}x + {b_2}y + {c_2} = 0\) ta xác định được tọa độ của vectơ \(\overrightarrow {{n_2}} \) là \(\left( {{a_2};{b_2}} \right)\).
+) \(\cos \left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right) = \frac{{\overrightarrow {{n_1}} .\overrightarrow {{n_2}} }}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}} = \frac{{{a_1}{a_2} + {b_1}{b_2}}}{{\sqrt {{a_1}^2 + {b_1}^2} \sqrt {{a_2}^2 + {b_2}^2} }}\).
Tìm số đo của góc giữa hai đường thẳng là đồ thị của hai hàm số \(y = x\) và \(y = 2x + 1\).
Phương pháp giải:
Bước 1: Viết phương trình tổng quat từ đồ thị của hai hàm số đã cho.
Bước 2: Xác định vectơ pháp tuyến.
Bước 3: \(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2}} \right|}}{{\sqrt {{a_1}^2 + {b_1}^2} \sqrt {{a_2}^2 + {b_2}^2} }}\).
Lời giải chi tiết:
Từ đồ thị hàm số ta có phương trình tổng quát:
\(y = x \Leftrightarrow {d_1}:x - y = 0\), \(y = 2x + 1 \Leftrightarrow 2x - y + 1 = 0\)
Từ đó ta có vectơ pháp tuyến lần lượt là \(\overrightarrow {{n_1}} = \left( {1; - 1} \right),\overrightarrow {{n_2}} = \left( {2; - 1} \right)\).
\(\cos \left( {{d_1},{d_2}} \right) = \frac{{\left| {1.2 + ( - 1).( - 1)} \right|}}{{\sqrt {{1^2} + {{\left( { - 1} \right)}^2}} \sqrt {{2^2} + {{\left( { - 1} \right)}^2}} }} = \frac{{3\sqrt {10} }}{{10}} \Rightarrow \left( {{d_1},{d_2}} \right) \approx 18^\circ 26'\).
Vậy góc giữa hai đường thẳng có đồ thị đã cho gần bằng \(18^\circ 26'\).
Tìm số đo của góc giữa hai đường thẳng \({\Delta _1}\)và \({\Delta _2}\) trong các trường hợp sau:
a) \({\Delta _1}:x + 3y - 7 = 0\) và \({\Delta _2}:x - 2y + 3 = 0\)
b) \({\Delta _1}:4x - 2y + 5 = 0\) và \({\Delta _2}:\left\{ \begin{array}{l}x = t\\y = 13 + 2t\end{array} \right.\)
c) \({\Delta _1}:\left\{ \begin{array}{l}x = 1 + t\\y = 3 + 2t\end{array} \right.\) và \({\Delta _2}:\left\{ \begin{array}{l}x = - 7 + 2t\\y = 1 - t\end{array} \right.\)
Phương pháp giải:
Bước 1: Xác định vectơ pháp tuyến của hai đường thẳng đã cho.
Bước 2: Tính số đo góc giữa hai đường thẳng bằng công thức \(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2}} \right|}}{{\sqrt {{a_1}^2 + {b_1}^2} \sqrt {{a_2}^2 + {b_2}^2} }}\).
Lời giải chi tiết:
a) Ta có vectơ pháp tuyến của hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) lần lượt là \(\overrightarrow {{n_1}} = \left( {1;3} \right),\overrightarrow {{n_2}} = \left( {1; - 2} \right)\).
Ta có \(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \frac{{\left| {1.1 + 3.( - 2)} \right|}}{{\sqrt {{1^2} + {3^2}} \sqrt {{1^2} + {{\left( { - 2} \right)}^2}} }} = \frac{{\sqrt 2 }}{2} \Rightarrow \left( {{\Delta _1},{\Delta _2}} \right) \approx 45^\circ\).
b) Ta có vectơ pháp tuyến của hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) lần lượt là \(\overrightarrow {{n_1}} = \left( {4; - 2} \right),\overrightarrow {{n_2}} = \left( {2; - 1} \right)\).
Ta có \(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \frac{{\left| {4.2 + ( - 2).( - 1)} \right|}}{{\sqrt {{4^2} + {{\left( { - 2} \right)}^2}} \sqrt {{2^2} + {{\left( { - 1} \right)}^2}} }} = 1 \Rightarrow \left( {{\Delta _1},{\Delta _2}} \right) = 0^\circ \).
c) Ta có vectơ pháp tuyến của hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) lần lượt là \(\overrightarrow {{n_1}} = \left( {2; - 1} \right),\overrightarrow {{n_2}} = \left( {1;2} \right)\).
Ta có \({a_1}{a_2} + {b_1}{b_2} = 2.1 + ( - 1).2 = 0\).
Suy ra \(\left( {{\Delta _1},{\Delta _2}} \right) = 90^\circ \).
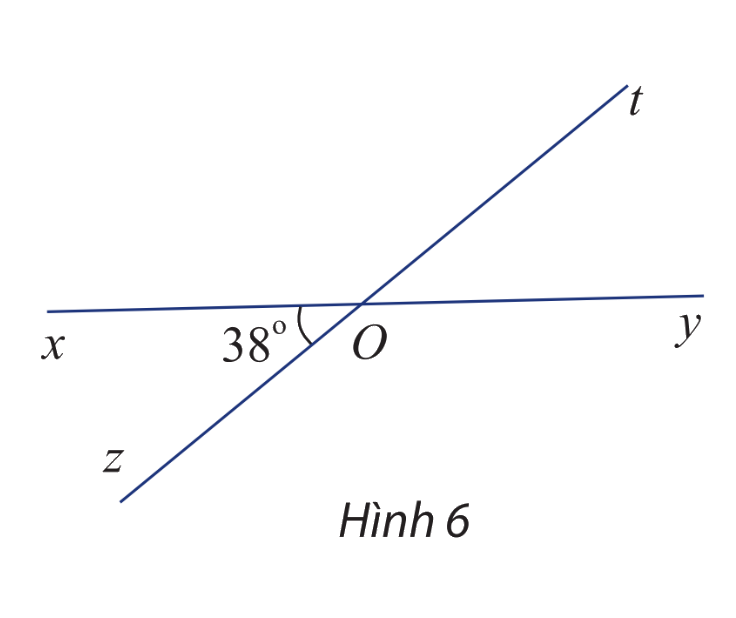
Cho hai đường thẳng xy và zt cắt nhau tại O và cho biết \(\widehat {xOz} = 38^\circ \) (hình 6).
Tính số đo các góc \(\widehat {xOt},\widehat {tOy}\) và \(\widehat {yOz}\).
Lời giải chi tiết:
Ta có hai góc \(\widehat {xOz}\) và \(\widehat {tOy}\) đối đỉnh nên \(\widehat {xOz} = \widehat {tOy} = 38^\circ \).
Hai góc \(\widehat {xOt}\) và \(\widehat {yOz}\) đối đỉnh nên \(\widehat {xOt} = \widehat {yOz}\).
Hai góc \(\widehat {xOz}\) và \(\widehat {xOt}\) bù nhau nên \(\widehat {xOt} = 180^\circ - \widehat {xOz} = 180^\circ - 38^\circ = 142^\circ \).
Vậy \(\widehat {xOz} = \widehat {tOy} = 38^\circ \) và \(\widehat {xOt} = \widehat {yOz} = 142^\circ \).
Cho hai đường thẳng
\({\Delta _1}:{a_1}x + {b_1}y + {c_1} = 0\) (\({a_1}^2 + {b_1}^2 > 0\)) và \({\Delta _2}:{a_2}x + {b_2}y + {c_2} = 0\) \(\left( {{a_2}^2 + {b_2}^2 > 0} \right)\)
có vectơ pháp tuyến lần lượt là \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \).
Tìm tọa độ \(\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} \) và tính \(\cos \left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right)\).
Phương pháp giải:
+) Tọa độ của \(\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} \) được xác định từ phương trình tổng quát của hai đường thẳng.
+) Áp dụng biểu thức tọa độ của vectơ trong mặt phẳng.
Lời giải chi tiết:
+) Từ phương trình \({\Delta _1}:{a_1}x + {b_1}y + {c_1} = 0\) ta xác định được tọa độ của vectơ \(\overrightarrow {{n_1}} \) là \(\left( {{a_1};{b_1}} \right)\).
+) Từ phương trình \({\Delta _2}:{a_2}x + {b_2}y + {c_2} = 0\) ta xác định được tọa độ của vectơ \(\overrightarrow {{n_2}} \) là \(\left( {{a_2};{b_2}} \right)\).
+) \(\cos \left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right) = \frac{{\overrightarrow {{n_1}} .\overrightarrow {{n_2}} }}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}} = \frac{{{a_1}{a_2} + {b_1}{b_2}}}{{\sqrt {{a_1}^2 + {b_1}^2} \sqrt {{a_2}^2 + {b_2}^2} }}\).
Tìm số đo của góc giữa hai đường thẳng \({\Delta _1}\)và \({\Delta _2}\) trong các trường hợp sau:
a) \({\Delta _1}:x + 3y - 7 = 0\) và \({\Delta _2}:x - 2y + 3 = 0\)
b) \({\Delta _1}:4x - 2y + 5 = 0\) và \({\Delta _2}:\left\{ \begin{array}{l}x = t\\y = 13 + 2t\end{array} \right.\)
c) \({\Delta _1}:\left\{ \begin{array}{l}x = 1 + t\\y = 3 + 2t\end{array} \right.\) và \({\Delta _2}:\left\{ \begin{array}{l}x = - 7 + 2t\\y = 1 - t\end{array} \right.\)
Phương pháp giải:
Bước 1: Xác định vectơ pháp tuyến của hai đường thẳng đã cho.
Bước 2: Tính số đo góc giữa hai đường thẳng bằng công thức \(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2}} \right|}}{{\sqrt {{a_1}^2 + {b_1}^2} \sqrt {{a_2}^2 + {b_2}^2} }}\).
Lời giải chi tiết:
a) Ta có vectơ pháp tuyến của hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) lần lượt là \(\overrightarrow {{n_1}} = \left( {1;3} \right),\overrightarrow {{n_2}} = \left( {1; - 2} \right)\).
Ta có \(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \frac{{\left| {1.1 + 3.( - 2)} \right|}}{{\sqrt {{1^2} + {3^2}} \sqrt {{1^2} + {{\left( { - 2} \right)}^2}} }} = \frac{{\sqrt 2 }}{2} \Rightarrow \left( {{\Delta _1},{\Delta _2}} \right) \approx 45^\circ\).
b) Ta có vectơ pháp tuyến của hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) lần lượt là \(\overrightarrow {{n_1}} = \left( {4; - 2} \right),\overrightarrow {{n_2}} = \left( {2; - 1} \right)\).
Ta có \(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \frac{{\left| {4.2 + ( - 2).( - 1)} \right|}}{{\sqrt {{4^2} + {{\left( { - 2} \right)}^2}} \sqrt {{2^2} + {{\left( { - 1} \right)}^2}} }} = 1 \Rightarrow \left( {{\Delta _1},{\Delta _2}} \right) = 0^\circ \).
c) Ta có vectơ pháp tuyến của hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) lần lượt là \(\overrightarrow {{n_1}} = \left( {2; - 1} \right),\overrightarrow {{n_2}} = \left( {1;2} \right)\).
Ta có \({a_1}{a_2} + {b_1}{b_2} = 2.1 + ( - 1).2 = 0\).
Suy ra \(\left( {{\Delta _1},{\Delta _2}} \right) = 90^\circ \).
Tìm số đo của góc giữa hai đường thẳng là đồ thị của hai hàm số \(y = x\) và \(y = 2x + 1\).
Phương pháp giải:
Bước 1: Viết phương trình tổng quat từ đồ thị của hai hàm số đã cho.
Bước 2: Xác định vectơ pháp tuyến.
Bước 3: \(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2}} \right|}}{{\sqrt {{a_1}^2 + {b_1}^2} \sqrt {{a_2}^2 + {b_2}^2} }}\).
Lời giải chi tiết:
Từ đồ thị hàm số ta có phương trình tổng quát:
\(y = x \Leftrightarrow {d_1}:x - y = 0\), \(y = 2x + 1 \Leftrightarrow 2x - y + 1 = 0\)
Từ đó ta có vectơ pháp tuyến lần lượt là \(\overrightarrow {{n_1}} = \left( {1; - 1} \right),\overrightarrow {{n_2}} = \left( {2; - 1} \right)\).
\(\cos \left( {{d_1},{d_2}} \right) = \frac{{\left| {1.2 + ( - 1).( - 1)} \right|}}{{\sqrt {{1^2} + {{\left( { - 1} \right)}^2}} \sqrt {{2^2} + {{\left( { - 1} \right)}^2}} }} = \frac{{3\sqrt {10} }}{{10}} \Rightarrow \left( {{d_1},{d_2}} \right) \approx 18^\circ 26'\).
Vậy góc giữa hai đường thẳng có đồ thị đã cho gần bằng \(18^\circ 26'\).
Cho hai đường thẳng xy và zt cắt nhau tại O và cho biết \(\widehat {xOz} = 38^\circ \) (hình 6).
Tính số đo các góc \(\widehat {xOt},\widehat {tOy}\) và \(\widehat {yOz}\).

Lời giải chi tiết:
Ta có hai góc \(\widehat {xOz}\) và \(\widehat {tOy}\) đối đỉnh nên \(\widehat {xOz} = \widehat {tOy} = 38^\circ \).
Hai góc \(\widehat {xOt}\) và \(\widehat {yOz}\) đối đỉnh nên \(\widehat {xOt} = \widehat {yOz}\).
Hai góc \(\widehat {xOz}\) và \(\widehat {xOt}\) bù nhau nên \(\widehat {xOt} = 180^\circ - \widehat {xOz} = 180^\circ - 38^\circ = 142^\circ \).
Vậy \(\widehat {xOz} = \widehat {tOy} = 38^\circ \) và \(\widehat {xOt} = \widehat {yOz} = 142^\circ \).
Mục 3 trong SGK Toán 10 tập 2 chương trình Chân trời sáng tạo thường xoay quanh các chủ đề về vectơ, các phép toán vectơ, và ứng dụng của vectơ trong hình học. Việc nắm vững kiến thức nền tảng và phương pháp giải bài tập trong mục này là vô cùng quan trọng để các em học sinh có thể giải quyết các bài toán phức tạp hơn trong các chương tiếp theo.
Để giải các bài tập trong mục 3, các em cần nắm vững các kiến thức lý thuyết đã học và áp dụng linh hoạt các công thức, định lý. Dưới đây là một số gợi ý cụ thể cho từng dạng bài:
Các bài tập dạng này thường yêu cầu các em xác định vectơ, tìm tọa độ vectơ, hoặc chứng minh sự bằng nhau của hai vectơ. Để giải các bài tập này, các em cần hiểu rõ định nghĩa vectơ và các yếu tố của vectơ.
Các bài tập dạng này thường yêu cầu các em thực hiện các phép cộng, trừ, nhân vectơ với một số thực. Để giải các bài tập này, các em cần nắm vững các quy tắc thực hiện các phép toán vectơ.
Các bài tập dạng này thường yêu cầu các em tính tích vô hướng của hai vectơ, tính góc giữa hai vectơ, hoặc kiểm tra xem hai vectơ có vuông góc hay không. Để giải các bài tập này, các em cần nắm vững định nghĩa và tính chất của tích vô hướng.
Các bài tập dạng này thường yêu cầu các em chứng minh các đẳng thức hình học, giải các bài toán liên quan đến tọa độ điểm và đường thẳng. Để giải các bài tập này, các em cần kết hợp kiến thức về vectơ với kiến thức về hình học.
Cho hai vectơ a = (1; 2) và b = (-3; 4). Tính a + b và a - b.
Lời giải:
a + b = (1 + (-3); 2 + 4) = (-2; 6)
a - b = (1 - (-3); 2 - 4) = (4; -2)
Ngoài SGK Toán 10 tập 2, các em có thể tham khảo thêm các tài liệu sau để nâng cao kiến thức và kỹ năng giải bài tập:
Hy vọng với những hướng dẫn chi tiết trên, các em học sinh sẽ tự tin giải quyết các bài tập trong mục 3 trang 54, 55, 56, 57 SGK Toán 10 tập 2 - Chân trời sáng tạo. Chúc các em học tập tốt!