Bài 7 trang 97 SGK Toán 10 tập 1 thuộc chương trình học Toán 10 Chân trời sáng tạo, yêu cầu học sinh vận dụng kiến thức về vectơ để giải quyết các bài toán liên quan đến hình học. Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Chúng tôi cung cấp không chỉ đáp án mà còn cả phương pháp giải, giúp các bạn hiểu rõ bản chất của bài toán và áp dụng vào các bài tập tương tự.
Cho tam giác ABC a) Xác định các điểm M, N, P thỏa mãn:
Đề bài
Cho tam giác ABC
a) Xác định các điểm M, N, P thỏa mãn: \(\overrightarrow {MB} = \frac{1}{2}\overrightarrow {BC} ,\overrightarrow {AN} = 3\overrightarrow {NB} ,\overrightarrow {CP} = \overrightarrow {PA} \)
b) Biểu thị mỗi vectơ \(\overrightarrow {MN} ,\overrightarrow {MP} \) theo hai vectơ \(\overrightarrow {BC} ,\overrightarrow {BA} \)
c) Chứng minh ba điểm M, N, P thẳng hàng
Phương pháp giải - Xem chi tiết
a) Xác định hướng và tỉ số độ dài
\(\overrightarrow {MB} = k.\overrightarrow {BC} \Rightarrow \overrightarrow {MB} \) và \(\overrightarrow {BC} \) cùng hướng; tỉ số độ dài \(\frac{{BC}}{{MB}} = k\)
b) Phân tích \(\overrightarrow {MN}\) theo hai vecto \(\overrightarrow {MB}, \overrightarrow {NB}\)
c) \(M,N,P\) thẳng hàng \( \Leftrightarrow \overrightarrow {MN} = k.\overrightarrow {MP} \) \(\left( k \in {\mathbb Z}^* \right)\)
Lời giải chi tiết
a) Ta có:
+) \(\overrightarrow {MB} = \dfrac{1}{2}\overrightarrow {BC} \Rightarrow \overrightarrow {MB} \) và \(\overrightarrow {BC} \) cùng hướng; tỉ số độ dài \(\dfrac{{BC}}{{MB}} = 2\)
\( \Rightarrow M\) nằm ngoài đoạn thẳng BC sao cho \(MB = \dfrac{1}{2}BC\)
+) \({\overrightarrow {AN} = 3\overrightarrow {NB} \Rightarrow \overrightarrow {AB} + \overrightarrow {BN} = 3\overrightarrow {NB} \Rightarrow 4\overrightarrow {NB} = \overrightarrow {AB} \Leftrightarrow \overrightarrow {NB} = \dfrac{1}{4}\overrightarrow {AB} }\)
\( \Rightarrow N\) thuộc đoạn thẳng AB và \(NB=\dfrac{{1}}{{4}} AB\)
+) \(\overrightarrow {CP} = \overrightarrow {PA} \Leftrightarrow \overrightarrow {PC} + \overrightarrow {PA} = \overrightarrow 0 \)
\( \Rightarrow P\)là trung điểm của CA
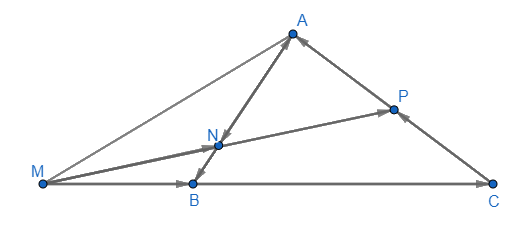
b) \(\overrightarrow {MN} = \overrightarrow {MB} + \overrightarrow {BN} = \frac{1}{2}\overrightarrow {BC} + \frac{1}{4}\overrightarrow {BA} \)
\(\begin{array}{l}\overrightarrow {MP} = \overrightarrow {MC} + \overrightarrow {CP} = \overrightarrow {MC} + \frac{1}{2}\overrightarrow {CA} \\= \frac{3}{2}\overrightarrow {BC} + \frac{1}{2}\left( {\overrightarrow {BA} - \overrightarrow {BC} } \right)\\ = \overrightarrow {BC} + \frac{1}{2}\overrightarrow {BA} \end{array}\)
c) Ta có:
\(\overrightarrow {MN} = \frac{1}{2}\overrightarrow {BC} + \frac{1}{4}\overrightarrow {BA} ;\) \(\overrightarrow {MP} = \overrightarrow {BC} + \frac{1}{2}\overrightarrow {BA} \)
\( \Rightarrow \overrightarrow {MP} = 2\overrightarrow {MN} \)
Vậy \(M,N,P\) thẳng hàng
Bài 7 trang 97 SGK Toán 10 tập 1 – Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về vectơ và ứng dụng trong hình học. Để giải bài tập này, học sinh cần nắm vững các khái niệm cơ bản về vectơ, các phép toán vectơ và các tính chất liên quan.
Bài 7 yêu cầu học sinh thực hiện các thao tác với vectơ, thường liên quan đến việc tìm tọa độ của vectơ, tính độ dài của vectơ, hoặc chứng minh các đẳng thức vectơ. Đề bài có thể đưa ra các hình vẽ minh họa hoặc các thông tin về vị trí tương đối của các điểm để học sinh suy luận và giải quyết.
Để giải bài 7 trang 97 SGK Toán 10 tập 1 – Chân trời sáng tạo, học sinh có thể áp dụng các phương pháp sau:
Giả sử đề bài yêu cầu tìm tọa độ của vectơ AB, biết A(xA, yA) và B(xB, yB). Khi đó, tọa độ của vectơ AB được tính theo công thức:
AB = (xB - xA, yB - yA)
Khi giải bài 7 trang 97 SGK Toán 10 tập 1 – Chân trời sáng tạo, học sinh cần lưu ý:
Để củng cố kiến thức về vectơ, học sinh có thể làm thêm các bài tập tương tự trong SGK Toán 10 tập 1 – Chân trời sáng tạo hoặc các bài tập luyện tập khác.
Giải bài 7 trang 97 SGK Toán 10 tập 1 – Chân trời sáng tạo đòi hỏi học sinh phải nắm vững kiến thức về vectơ và áp dụng linh hoạt các phương pháp giải. Giaitoan.edu.vn hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải quyết bài tập và đạt kết quả tốt trong môn Toán 10.
| Khái niệm | Giải thích |
|---|---|
| Vectơ | Một đoạn thẳng có hướng. |
| Tọa độ vectơ | Cặp số thực biểu diễn vectơ trong hệ tọa độ. |
| Độ dài vectơ | Khoảng cách giữa điểm đầu và điểm cuối của vectơ. |
| Bảng tóm tắt các khái niệm quan trọng. | |