Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10 tập 2. Bài viết này sẽ hướng dẫn bạn giải bài 6 trang 18 SGK Toán 10 tập 2 – Chân trời sáng tạo một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập môn Toán.
Một quả bóng được bắn thẳng lên từ độ cao 2 m với vận tốc ban đầu là 30 m/s. Khoảng cách quả bóng so với mặt đất t giây được cho bởi hàm số:
Đề bài
Một quả bóng được bắn thẳng lên từ độ cao 2 m với vận tốc ban đầu là 30 m/s. Khoảng cách quả bóng so với mặt đất t giây được cho bởi hàm số:
\(h\left( t \right) = - 4,9{t^2} + 30t + 2\)
với \(h\left( t \right)\) tính bằng đơn vị mét. Hỏi quả bóng nằm ở độ cao trên 40 m trong thời gian bao lâu? Làm tròn kết quả đến hàng phần mười.
Phương pháp giải - Xem chi tiết
Bước 1: Từ giả thiết lập bất phương trình.
Bước 2: Giải bất phương trình vừa tìm được.
Lời giải chi tiết
Theo giả thiết, khoảng thời gian bóng nằm ở độ cao 40 m là nghiệm của bất phương trình sau:
\(\begin{array}{l}h\left( t \right) > 40 \Leftrightarrow - 4,9{t^2} + 30t + 2 > 40\\ \Leftrightarrow - 4,9{t^2} + 30t - 38 > 0\end{array}\)
Xét tam thức \(f\left( t \right) = - 4,9{t^2} + 30t - 38\) có \(\Delta = 155,2 > 0\), có hai nghiệm phân biệt là \({x_1} \simeq 1,8;{x_2} \simeq 4,3\) và có \(a = - 4,9 < 0\)
Ta có bảng xét dấu như sau:
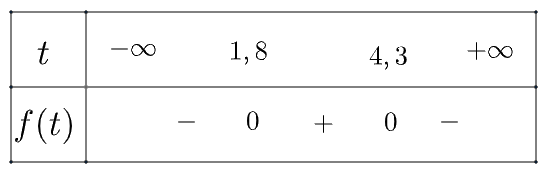
Từ đó cho thấy khoảng từ 1,8 s đến 4,3 s lag khoảng thời gian bóng cao so với mặt đất lớn hơn 40 m
Vậy quả bóng nằm ở độ cao trên 40 m trong thời gian 2,5 giây.
Bài 6 trang 18 SGK Toán 10 tập 2 – Chân trời sáng tạo thuộc chương trình học Toán 10, tập trung vào việc vận dụng các kiến thức về vectơ để giải quyết các bài toán hình học. Bài tập này yêu cầu học sinh hiểu rõ các khái niệm như vectơ, phép cộng, phép trừ vectơ, tích của một số với vectơ, và các tính chất liên quan.
Bài 6 bao gồm các dạng bài tập sau:
Đề bài: Cho hình bình hành ABCD. Tìm vectơ bằng vectơ AB.
Lời giải: Trong hình bình hành ABCD, ta có AB = DC và AB // DC. Do đó, vectơ bằng vectơ AB là vectơ DC.
Đề bài: Tìm vectơ đối của vectơ AD.
Lời giải: Vectơ đối của vectơ AD là vectơ -AD. Trong hình bình hành ABCD, ta có AD = BC và AD // BC. Do đó, vectơ đối của vectơ AD là vectơ -BC.
Đề bài: Tìm tổng của vectơ AB và vectơ AD.
Lời giải: Tổng của vectơ AB và vectơ AD là vectơ AB + AD. Trong hình bình hành ABCD, vectơ AB + AD = AC (quy tắc hình bình hành).
Để giải quyết bài 6 trang 18 SGK Toán 10 tập 2 – Chân trời sáng tạo một cách hiệu quả, bạn cần nắm vững các kiến thức sau:
Dưới đây là một số mẹo giúp bạn giải bài tập vectơ một cách dễ dàng hơn:
Để củng cố kiến thức về vectơ, bạn có thể làm thêm các bài tập tương tự sau:
Bài 6 trang 18 SGK Toán 10 tập 2 – Chân trời sáng tạo là một bài tập quan trọng giúp bạn hiểu rõ hơn về vectơ và các phép toán vectơ. Hy vọng với lời giải chi tiết và các kiến thức bổ ích trên, bạn sẽ tự tin hơn trong quá trình học tập môn Toán.