Chào mừng các em học sinh đến với bài giải Hoạt động 1 trang 92, 93 SGK Toán 10 tập 2 - Chân trời sáng tạo. Bài viết này cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và hoàn thành bài tập một cách hiệu quả.
Giaitoan.edu.vn là địa chỉ học toán online uy tín, cung cấp đầy đủ các bài giải SGK Toán 10, bài tập trắc nghiệm, và các tài liệu học tập hữu ích khác.
Vẽ các elip sau Thiết kế một đường hầm có mặt cắt hình nửa elip cao 4 m, rộng 10 m
Thiết kế một đường hầm có mặt cắt hình nửa elip cao 4 m, rộng 10 m
Phương pháp giải:
Từ chiều rộng và chiều cao xác định a, b. Từ đó xác định công thức elip và hình dạng
Lời giải chi tiết:
Ta có: Chiều cao và chiều rộng của đường hầm là 4m, 10m nên ta có: \(a = 5,b = 4\)
Nên phương trình chính tắc của elip có dạng \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\)
Nhập phương trình elip theo cú pháp x^2/25 + y^2/16 = 1 {y>=0} vào vùng nhập lệnh ta có hình vẽ mô phỏng đường hầm dưới đây
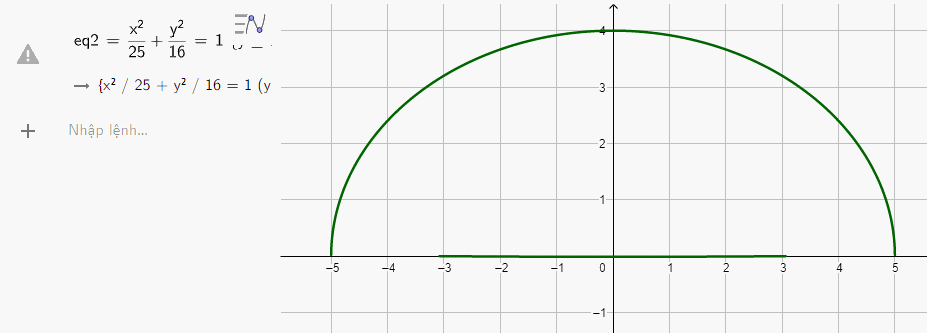
Vậy phương trình mô phỏng đường hầm là \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\) với \(y \ge 0\)
Và có hình mô phỏng thực tế như hình trên
Vẽ các elip sau
a) \(\frac{{{x^2}}}{{10}} + \frac{{{y^2}}}{4} = 1\)
b) \(\frac{{{x^2}}}{{12}} + \frac{{{y^2}}}{3} = 1\)
c) \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{36}} = 1\)
Phương pháp giải:
Bước 1: Khởi động phần mềm Geogebra
Bước 2: Nhập phương trình elip \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) theo cú pháp x^2/a^2 + y^2/b^2 = 1 vào vùng nhập lệnh
Bước 3: Quan sát hình vẽ xuất hiện trên vùng làm việc
Lời giải chi tiết:
Thực hiện các bước đã nêu ở phương pháp ta có
a) Nhập phương trình elip theo cú pháp x^2/10 + y^2/4 = 1 vào vùng nhập lệnh ta được hình elip dưới đây:
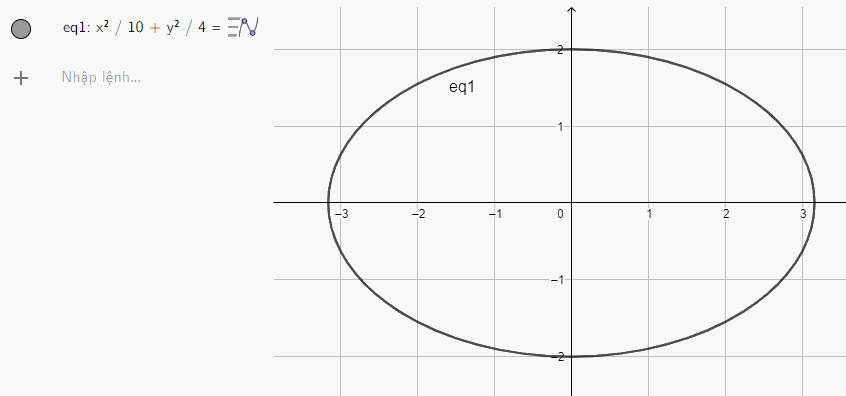
b) Nhập phương trình elip theo cú pháp x^2/12 + y^2/3 = 1 vào vùng nhập lệnh ta được hình elip dưới đây:
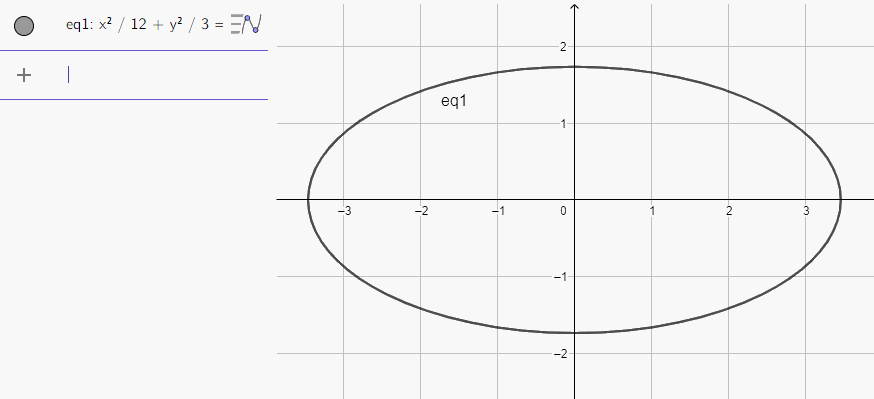
c) Nhập phương trình elip theo cú pháp x^2/100 + y^2/36 = 1 vào vùng nhập lệnh ta được hình elip dưới đây:
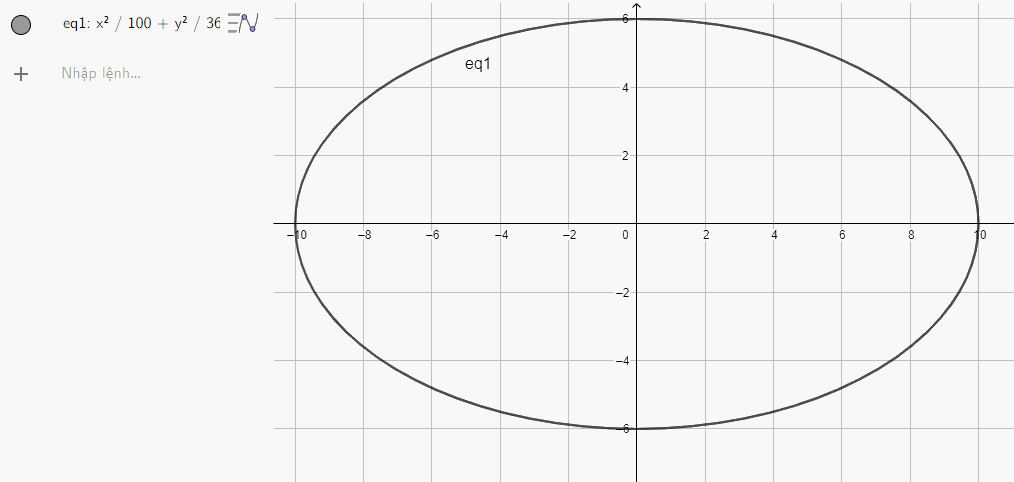
Vẽ các elip sau
a) \(\frac{{{x^2}}}{{10}} + \frac{{{y^2}}}{4} = 1\)
b) \(\frac{{{x^2}}}{{12}} + \frac{{{y^2}}}{3} = 1\)
c) \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{36}} = 1\)
Phương pháp giải:
Bước 1: Khởi động phần mềm Geogebra
Bước 2: Nhập phương trình elip \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) theo cú pháp x^2/a^2 + y^2/b^2 = 1 vào vùng nhập lệnh
Bước 3: Quan sát hình vẽ xuất hiện trên vùng làm việc
Lời giải chi tiết:
Thực hiện các bước đã nêu ở phương pháp ta có
a) Nhập phương trình elip theo cú pháp x^2/10 + y^2/4 = 1 vào vùng nhập lệnh ta được hình elip dưới đây:
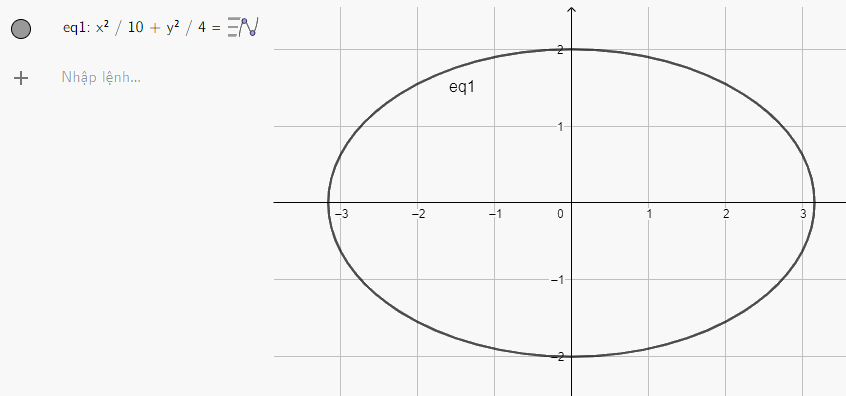
b) Nhập phương trình elip theo cú pháp x^2/12 + y^2/3 = 1 vào vùng nhập lệnh ta được hình elip dưới đây:
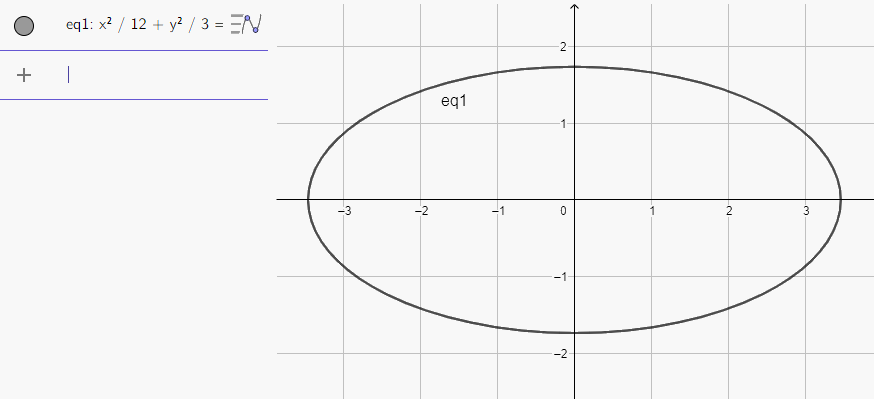
c) Nhập phương trình elip theo cú pháp x^2/100 + y^2/36 = 1 vào vùng nhập lệnh ta được hình elip dưới đây:
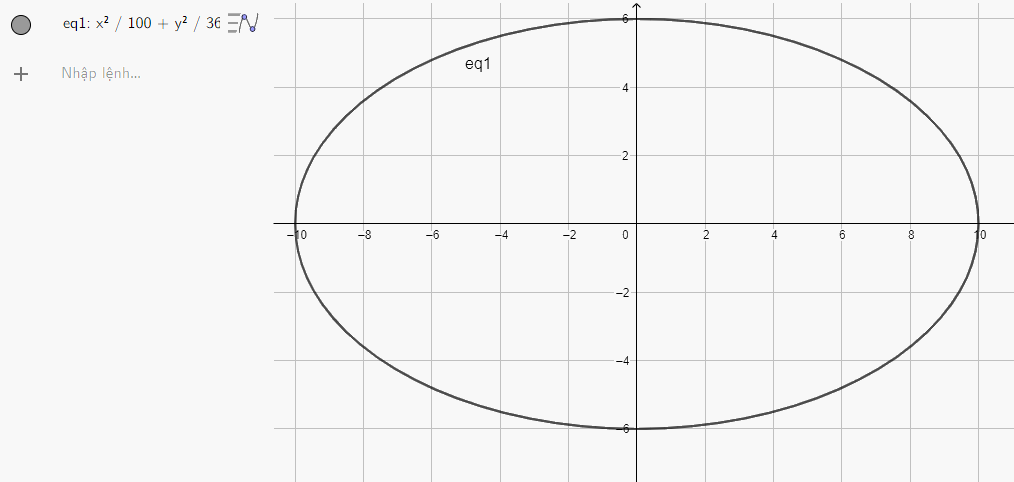
Thiết kế một đường hầm có mặt cắt hình nửa elip cao 4 m, rộng 10 m
Phương pháp giải:
Từ chiều rộng và chiều cao xác định a, b. Từ đó xác định công thức elip và hình dạng
Lời giải chi tiết:
Ta có: Chiều cao và chiều rộng của đường hầm là 4m, 10m nên ta có: \(a = 5,b = 4\)
Nên phương trình chính tắc của elip có dạng \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\)
Nhập phương trình elip theo cú pháp x^2/25 + y^2/16 = 1 {y>=0} vào vùng nhập lệnh ta có hình vẽ mô phỏng đường hầm dưới đây
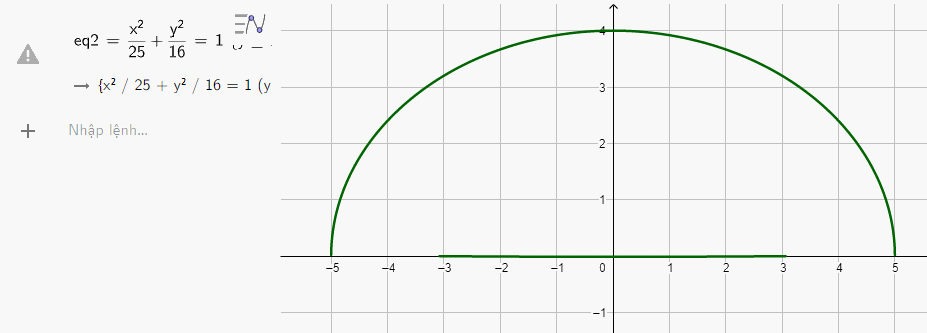
Vậy phương trình mô phỏng đường hầm là \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\) với \(y \ge 0\)
Và có hình mô phỏng thực tế như hình trên
Hoạt động 1 trang 92, 93 SGK Toán 10 tập 2 - Chân trời sáng tạo thuộc chương trình học về vectơ trong mặt phẳng. Hoạt động này yêu cầu học sinh vận dụng kiến thức về vectơ, phép cộng, phép trừ vectơ, và tích của một số với vectơ để giải quyết các bài toán thực tế. Việc nắm vững kiến thức này là nền tảng quan trọng cho việc học tập các chương trình Toán học ở các lớp trên.
Hoạt động 1 bao gồm các bài tập nhỏ, yêu cầu học sinh thực hiện các thao tác sau:
Để xác định các vectơ trong hình vẽ, học sinh cần nắm vững khái niệm về vectơ, chiều của vectơ, và điểm đầu, điểm cuối của vectơ. Sử dụng ký hiệu vectơ để biểu diễn các vectơ trong hình.
Phép cộng, phép trừ vectơ được thực hiện theo quy tắc hình bình hành hoặc quy tắc tam giác. Học sinh cần hiểu rõ quy tắc này để thực hiện các phép toán một cách chính xác. Ví dụ, cho hai vectơ a và b, vectơ tổng a + b là vectơ có điểm đầu là điểm đầu của a và điểm cuối là điểm cuối của b (hoặc ngược lại).
Tọa độ của vectơ được xác định bằng hiệu tọa độ của điểm cuối và điểm đầu. Ví dụ, cho điểm A(xA, yA) và điểm B(xB, yB), vectơ AB có tọa độ là (xB - xA, yB - yA).
Các bài toán ứng dụng liên quan đến vectơ thường xuất hiện trong các lĩnh vực như vật lý, kỹ thuật, và hình học. Học sinh cần vận dụng kiến thức về vectơ để giải quyết các bài toán này một cách hiệu quả. Ví dụ, bài toán về lực tác dụng lên một vật có thể được giải bằng cách sử dụng vectơ để biểu diễn các lực này.
Ngoài SGK Toán 10 tập 2 - Chân trời sáng tạo, học sinh có thể tham khảo thêm các tài liệu sau:
Hy vọng bài giải Hoạt động 1 trang 92, 93 SGK Toán 10 tập 2 - Chân trời sáng tạo này sẽ giúp các em học sinh hiểu rõ hơn về vectơ và các phép toán liên quan. Chúc các em học tập tốt!