Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 65, 66, 67 sách giáo khoa Toán 10 tập 1 - Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong học tập.
Tính khoảng cách giữa hai điểm ở hai đầu của một hồ nước. Biết từ một điểm cách hai đầu hồ lần lượt là 880 m và 900 m người quan sát nhìn hai điểm này dưới một góc 70 (Hình 5).
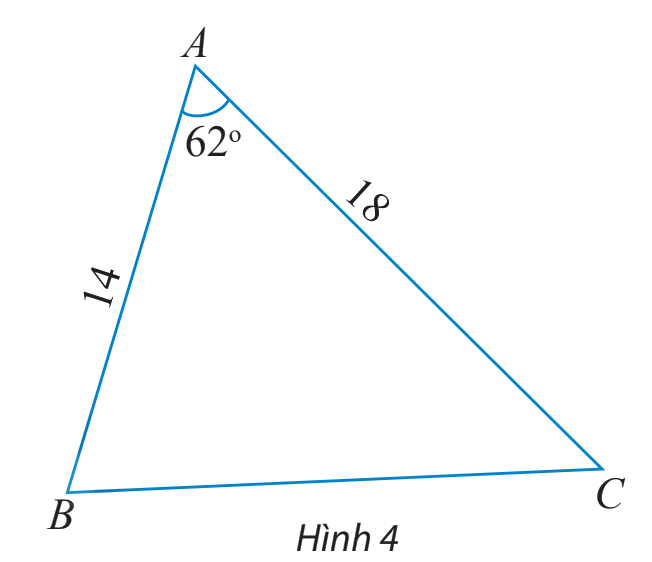
Tính các cạnh và các góc chưa biết của tam giác ABC trong hình 4.
Phương pháp giải:
Áp dụng định lí cosin trong tam giác ABC, ta có:
\(\begin{array}{l}B{C^2} = A{C^2} + A{B^2} - 2AC.AB\cos A\\\cos B = \frac{{A{B^2} + B{C^2} - A{C^2}}}{{2.AB.BC}};\cos C = \frac{{A{C^2} + B{C^2} - A{B^2}}}{{2.AC.BC}}\end{array}\)
Lời giải chi tiết:
Áp dụng định lí cosin trong tam giác ABC, ta có:
\(B{C^2} = A{C^2} + A{B^2} - 2AC.AB\cos A\)
Mà \(AB = 14,AC = 18,\widehat A = {62^o}\)
\(\begin{array}{l} \Rightarrow B{C^2} = {18^2} + {14^2} - 2.18.14\cos {62^o} \approx 283,3863\\ \Leftrightarrow BC \approx 16,834\end{array}\)
Lại có: Từ định lí cosin ta suy ra:
\(\cos B = \frac{{A{B^2} + B{C^2} - A{C^2}}}{{2.AB.BC}};\cos C = \frac{{A{C^2} + B{C^2} - A{B^2}}}{{2.AC.BC}}\)
\( \Rightarrow \left\{ \begin{array}{l}\cos B = \frac{{{{14}^2} + 16,{{834}^2} - {{18}^2}}}{{2.14.16,834}} \approx 0,3297\\\cos C = \frac{{{{18}^2} + 16,{{834}^2} - {{14}^2}}}{{2.18.16,834}} \approx 0,6788\end{array} \right.\)
\( \Rightarrow \left\{ \begin{array}{l}\widehat B \approx {70^o}45'\\\widehat C \approx {47^o}15'\end{array} \right.\)
Vậy \(BC \approx 16,834;\widehat B \approx {70^o}45';\widehat C \approx {47^o}15'.\)
Phương pháp giải:
Với \(\widehat A = {90^o}\) ta sử dụng định lí Pytago.
Với \(\widehat A \ne {90^o}\): Áp dụng định lí cosin: \({a^2} = {b^2} + {c^2} - 2bc\cos A\)
Lời giải chi tiết:
Áp dụng định lí Pytago, ta có:
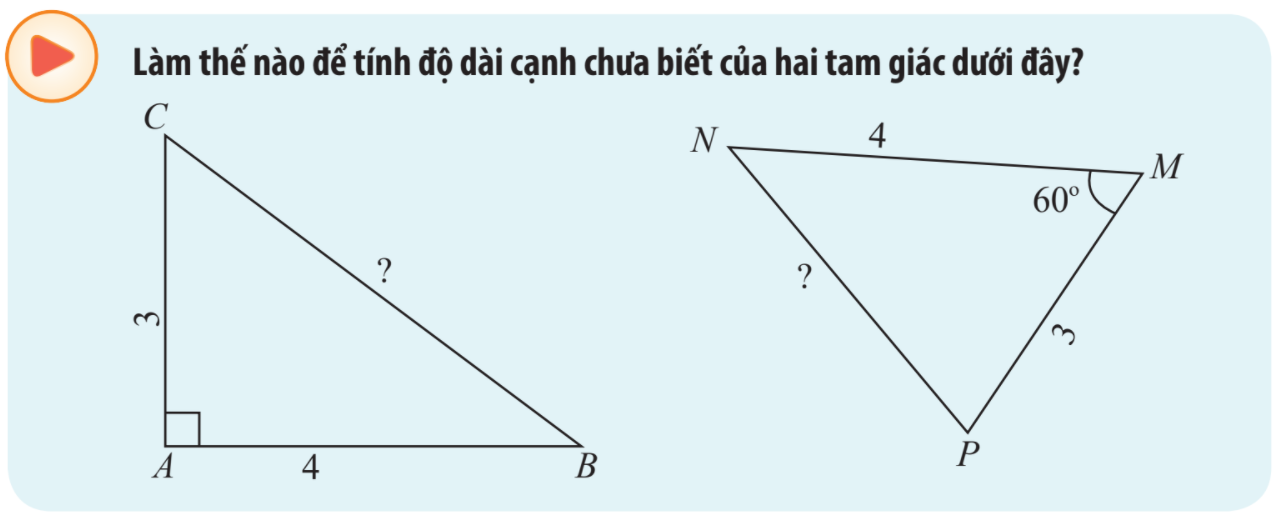
\(\begin{array}{l}B{C^2} = A{C^2} + A{B^2} = {3^2} + {4^2} = 25\\ \Rightarrow BC = 5\end{array}\)
Áp dụng định lí cosin trong tam giác MNP, ta có:
\(N{P^2} = M{N^2} + M{P^2} - 2.MN.MP\cos M\)
Mà \(MN = 4,MP = 3,\widehat M = {60^o}\)
\(\begin{array}{l} \Rightarrow N{P^2} = {4^2} + {3^2} - 2.4.3\cos {60^o} = 13\\ \Leftrightarrow NP = \sqrt {13} \approx 3,6\end{array}\)
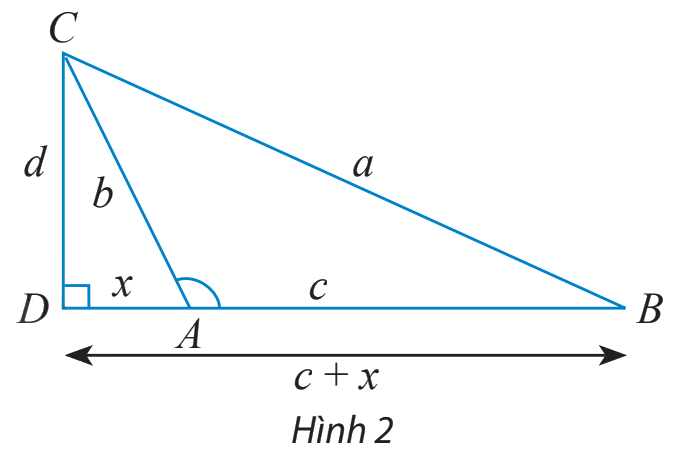
a) Cho tam giác ABC không phải là tam giác vuông với góc A nhọn và \(\widehat C \ge \widehat B.\) Vẽ đường cao CD và đặt tên các độ dài như trong Hình 1.
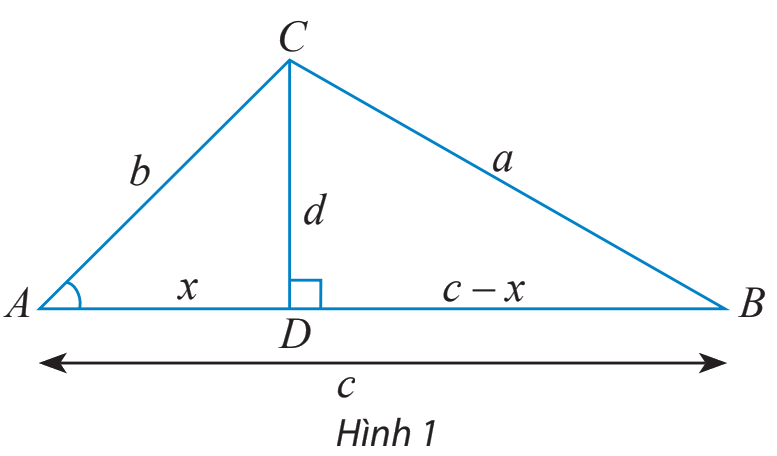
Hãy thay ? bằng các chữ cáu thích hợp để chứng minh công thức \({a^2} = {b^2} + {c^2} - 2bc\cos A\) theo gợi ý sau:
Xét tam giác vuông BCD, ta có: \({a^2} = {d^2} + {(c - x)^2} = {d^2} + {x^2} + {c^2} - 2xc\) (1)
Xét tam giác vuông ACD, ta có: \({b^2} = {d^2} + {x^2} \Rightarrow {d^2} = {b^2} - {x^2}\) (2)
\(\cos A = \frac{?}{b} \Rightarrow ? = b\cos A.\) (3)
Thay (2) và (3) vào (1), ta có: \({a^2} = {b^2} + {c^2} - 2bc\cos A\)
Lưu ý: Nếu \(\widehat B > \widehat C\) thì ta vẽ đường cao BD và chứng minh tương tự.
b) Cho tam giác ABC với góc A tù. Làm tương tự như trên, chứng minh rằng ta cũng có:
\({a^2} = {b^2} + {c^2} - 2bc\cos A\)
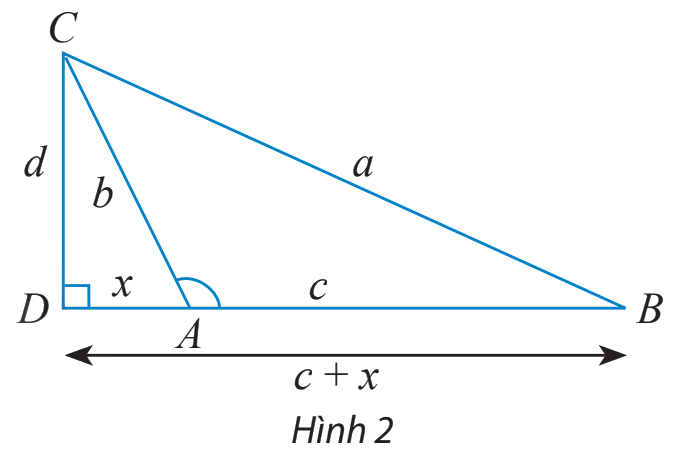
Lưu ý: Vì A là góc tù nên \(\cos A = - \frac{x}{b}.\)
c) Cho tam giác ABC vuông tại A. Hãy chứng tỏ coogn thức \({a^2} = {b^2} + {c^2} - 2bc\cos A\) có thể viết là \({a^2} = {b^2} + {c^2}.\)
Lời giải chi tiết:
a) ? = x vì \(\cos A = \frac{{AD}}{{AC}} = \frac{x}{b} \Rightarrow ? = x.\)
b) Xét tam giác vuông BCD, ta có: \({a^2} = {d^2} + {(c + x)^2} = {d^2} + {x^2} + {c^2} + 2xc\) (1)
Xét tam giác vuông ACD, ta có: \({b^2} = {d^2} + {x^2} \Rightarrow {d^2} = {b^2} - {x^2}\) (2)
\(\cos A = - \cos \widehat {DAC} = - \frac{x}{b} \Rightarrow x = - b\cos A.\) (3)
Thay (2) và (3) vào (1), ta có: \({a^2} = {b^2} + {c^2} - 2bc\cos A\)
c) Ta có: \({a^2} = {b^2} + {c^2} - 2bc\cos A\)
Mà \(\widehat A = {90^o} \Rightarrow \cos A = \cos {90^o} = 0.\)
\( \Rightarrow {a^2} = {b^2} + {c^2}\)
Tính khoảng cách giữa hai điểm ở hai đầu của một hồ nước. Biết từ một điểm cách hai đầu hồ lần lượt là 800 m và 900 m người quan sát nhìn hai điểm này dưới một góc \({70^o}\) (Hình 5).
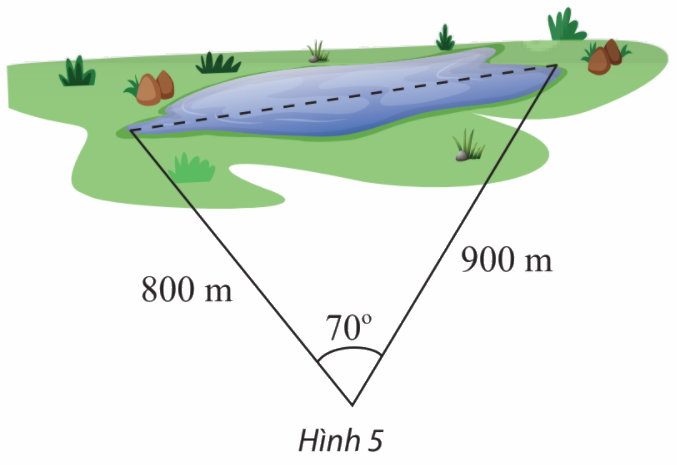
Phương pháp giải:
Áp dụng định lí cosin \({a^2} = {b^2} + {c^2} - 2bc\cos A\)
Lời giải chi tiết:
Kí hiệu hai vị trí đầu hồ và vị trí quan sát lần lượt bở các điểm A, B, C như hình dưới:
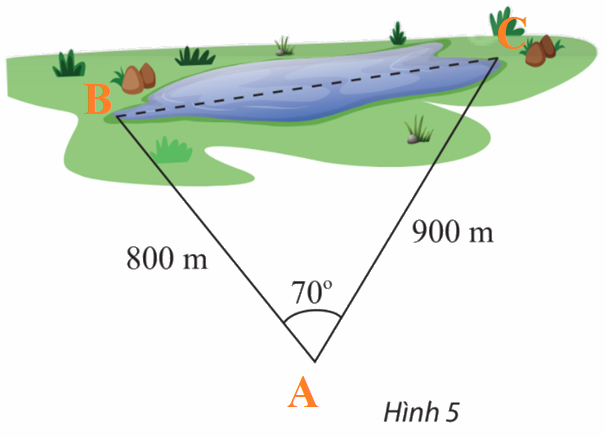
Áp dụng định lí cosin trong tam giác ABC, ta có:
\(B{C^2} = A{C^2} + A{B^2} - 2AC.AB\cos A\)
Mà \(AB = 800,AC = 900,\widehat A = {70^o}\)
\(\begin{array}{l} \Rightarrow B{C^2} = {900^2} + {800^2} - 2.900.800\cos {70^o} \approx 957490,9936\\ \Leftrightarrow BC \approx 978,5147\end{array}\)
Vậy khoảng cách giữa hai điểm ở hai đầu hồ là 978,5147 m.
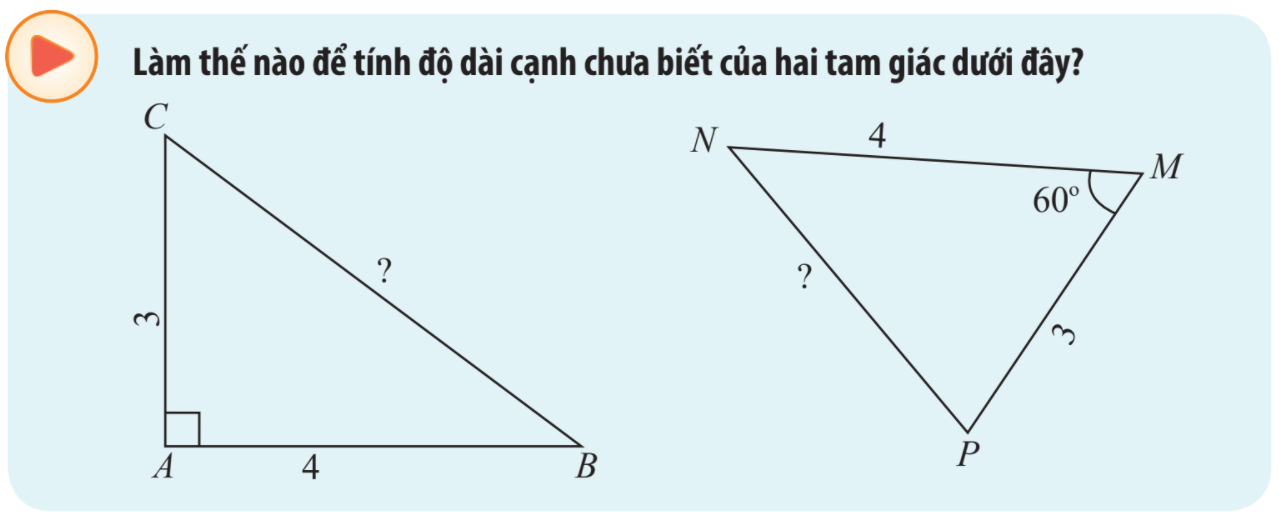
Phương pháp giải:
Với \(\widehat A = {90^o}\) ta sử dụng định lí Pytago.
Với \(\widehat A \ne {90^o}\): Áp dụng định lí cosin: \({a^2} = {b^2} + {c^2} - 2bc\cos A\)
Lời giải chi tiết:
Áp dụng định lí Pytago, ta có:
\(\begin{array}{l}B{C^2} = A{C^2} + A{B^2} = {3^2} + {4^2} = 25\\ \Rightarrow BC = 5\end{array}\)
Áp dụng định lí cosin trong tam giác MNP, ta có:
\(N{P^2} = M{N^2} + M{P^2} - 2.MN.MP\cos M\)
Mà \(MN = 4,MP = 3,\widehat M = {60^o}\)
\(\begin{array}{l} \Rightarrow N{P^2} = {4^2} + {3^2} - 2.4.3\cos {60^o} = 13\\ \Leftrightarrow NP = \sqrt {13} \approx 3,6\end{array}\)
a) Cho tam giác ABC không phải là tam giác vuông với góc A nhọn và \(\widehat C \ge \widehat B.\) Vẽ đường cao CD và đặt tên các độ dài như trong Hình 1.
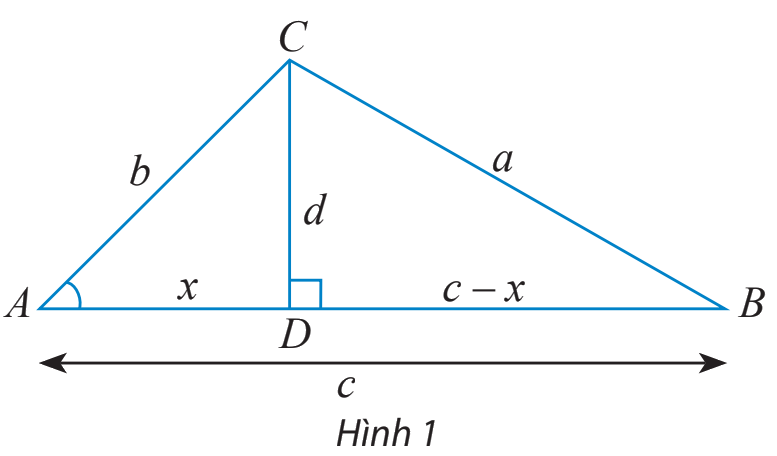
Hãy thay ? bằng các chữ cáu thích hợp để chứng minh công thức \({a^2} = {b^2} + {c^2} - 2bc\cos A\) theo gợi ý sau:
Xét tam giác vuông BCD, ta có: \({a^2} = {d^2} + {(c - x)^2} = {d^2} + {x^2} + {c^2} - 2xc\) (1)
Xét tam giác vuông ACD, ta có: \({b^2} = {d^2} + {x^2} \Rightarrow {d^2} = {b^2} - {x^2}\) (2)
\(\cos A = \frac{?}{b} \Rightarrow ? = b\cos A.\) (3)
Thay (2) và (3) vào (1), ta có: \({a^2} = {b^2} + {c^2} - 2bc\cos A\)
Lưu ý: Nếu \(\widehat B > \widehat C\) thì ta vẽ đường cao BD và chứng minh tương tự.
b) Cho tam giác ABC với góc A tù. Làm tương tự như trên, chứng minh rằng ta cũng có:
\({a^2} = {b^2} + {c^2} - 2bc\cos A\)
Lưu ý: Vì A là góc tù nên \(\cos A = - \frac{x}{b}.\)
c) Cho tam giác ABC vuông tại A. Hãy chứng tỏ coogn thức \({a^2} = {b^2} + {c^2} - 2bc\cos A\) có thể viết là \({a^2} = {b^2} + {c^2}.\)
Lời giải chi tiết:
a) ? = x vì \(\cos A = \frac{{AD}}{{AC}} = \frac{x}{b} \Rightarrow ? = x.\)
b) Xét tam giác vuông BCD, ta có: \({a^2} = {d^2} + {(c + x)^2} = {d^2} + {x^2} + {c^2} + 2xc\) (1)
Xét tam giác vuông ACD, ta có: \({b^2} = {d^2} + {x^2} \Rightarrow {d^2} = {b^2} - {x^2}\) (2)
\(\cos A = - \cos \widehat {DAC} = - \frac{x}{b} \Rightarrow x = - b\cos A.\) (3)
Thay (2) và (3) vào (1), ta có: \({a^2} = {b^2} + {c^2} - 2bc\cos A\)
c) Ta có: \({a^2} = {b^2} + {c^2} - 2bc\cos A\)
Mà \(\widehat A = {90^o} \Rightarrow \cos A = \cos {90^o} = 0.\)
\( \Rightarrow {a^2} = {b^2} + {c^2}\)
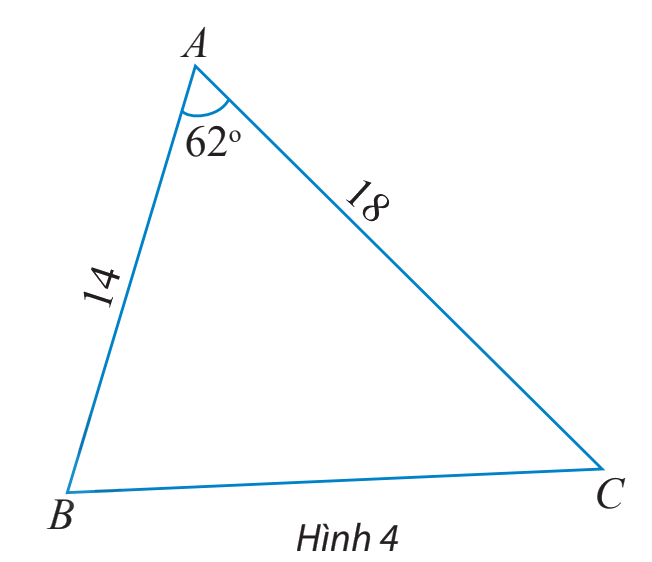
Tính các cạnh và các góc chưa biết của tam giác ABC trong hình 4.
Phương pháp giải:
Áp dụng định lí cosin trong tam giác ABC, ta có:
\(\begin{array}{l}B{C^2} = A{C^2} + A{B^2} - 2AC.AB\cos A\\\cos B = \frac{{A{B^2} + B{C^2} - A{C^2}}}{{2.AB.BC}};\cos C = \frac{{A{C^2} + B{C^2} - A{B^2}}}{{2.AC.BC}}\end{array}\)
Lời giải chi tiết:
Áp dụng định lí cosin trong tam giác ABC, ta có:
\(B{C^2} = A{C^2} + A{B^2} - 2AC.AB\cos A\)
Mà \(AB = 14,AC = 18,\widehat A = {62^o}\)
\(\begin{array}{l} \Rightarrow B{C^2} = {18^2} + {14^2} - 2.18.14\cos {62^o} \approx 283,3863\\ \Leftrightarrow BC \approx 16,834\end{array}\)
Lại có: Từ định lí cosin ta suy ra:
\(\cos B = \frac{{A{B^2} + B{C^2} - A{C^2}}}{{2.AB.BC}};\cos C = \frac{{A{C^2} + B{C^2} - A{B^2}}}{{2.AC.BC}}\)
\( \Rightarrow \left\{ \begin{array}{l}\cos B = \frac{{{{14}^2} + 16,{{834}^2} - {{18}^2}}}{{2.14.16,834}} \approx 0,3297\\\cos C = \frac{{{{18}^2} + 16,{{834}^2} - {{14}^2}}}{{2.18.16,834}} \approx 0,6788\end{array} \right.\)
\( \Rightarrow \left\{ \begin{array}{l}\widehat B \approx {70^o}45'\\\widehat C \approx {47^o}15'\end{array} \right.\)
Vậy \(BC \approx 16,834;\widehat B \approx {70^o}45';\widehat C \approx {47^o}15'.\)
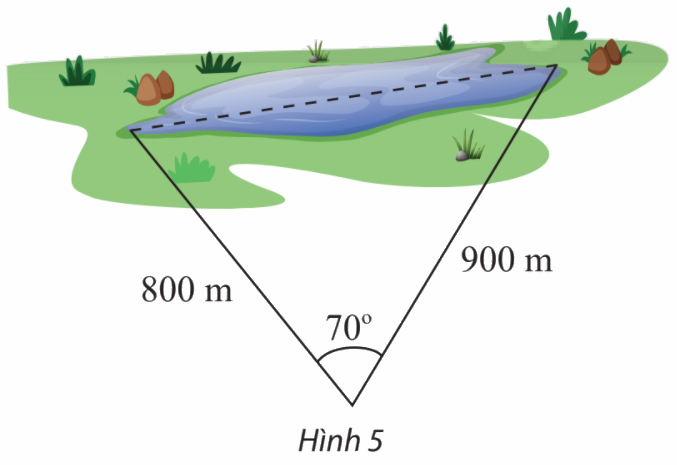
Tính khoảng cách giữa hai điểm ở hai đầu của một hồ nước. Biết từ một điểm cách hai đầu hồ lần lượt là 800 m và 900 m người quan sát nhìn hai điểm này dưới một góc \({70^o}\) (Hình 5).
Phương pháp giải:
Áp dụng định lí cosin \({a^2} = {b^2} + {c^2} - 2bc\cos A\)
Lời giải chi tiết:
Kí hiệu hai vị trí đầu hồ và vị trí quan sát lần lượt bở các điểm A, B, C như hình dưới:
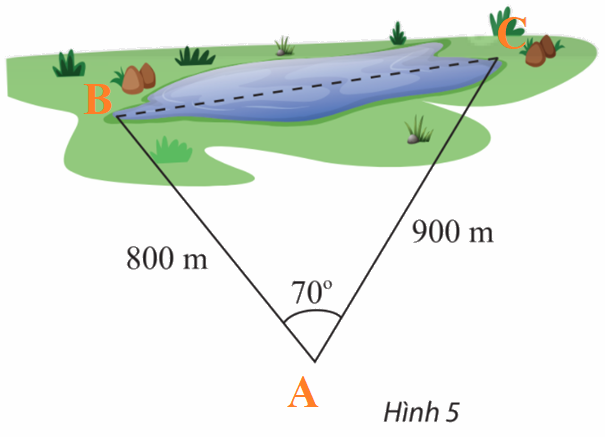
Áp dụng định lí cosin trong tam giác ABC, ta có:
\(B{C^2} = A{C^2} + A{B^2} - 2AC.AB\cos A\)
Mà \(AB = 800,AC = 900,\widehat A = {70^o}\)
\(\begin{array}{l} \Rightarrow B{C^2} = {900^2} + {800^2} - 2.900.800\cos {70^o} \approx 957490,9936\\ \Leftrightarrow BC \approx 978,5147\end{array}\)
Vậy khoảng cách giữa hai điểm ở hai đầu hồ là 978,5147 m.
Mục 1 của chương trình Toán 10 tập 1 - Chân trời sáng tạo tập trung vào việc ôn tập và mở rộng kiến thức về tập hợp, các phép toán trên tập hợp, và các khái niệm cơ bản về số thực. Việc nắm vững những kiến thức này là nền tảng quan trọng cho việc học tập các chương tiếp theo.
Các bài tập trên trang 65 thường xoay quanh việc xác định các tập hợp, tìm các phần tử thuộc tập hợp, và thực hiện các phép toán hợp, giao, hiệu của các tập hợp. Ví dụ, bài 1 yêu cầu xác định các tập hợp A, B, C dựa trên các điều kiện cho trước. Để giải bài này, học sinh cần hiểu rõ định nghĩa của tập hợp và cách xác định các phần tử thuộc tập hợp.
Trang 66 tiếp tục củng cố kiến thức về các phép toán trên tập hợp, đồng thời giới thiệu các tính chất của các phép toán này. Bài 2 yêu cầu chứng minh các đẳng thức liên quan đến phép hợp, giao, hiệu của các tập hợp. Để giải bài này, học sinh cần vận dụng các tính chất của các phép toán và sử dụng các quy tắc logic.
Các bài tập trên trang 67 thường mang tính ứng dụng cao hơn, yêu cầu học sinh vận dụng kiến thức về tập hợp và các phép toán để giải quyết các bài toán thực tế. Ví dụ, bài 3 yêu cầu giải một bài toán liên quan đến việc khảo sát sở thích của học sinh trong lớp. Để giải bài này, học sinh cần sử dụng sơ đồ Venn để biểu diễn các tập hợp và tính toán số lượng phần tử trong mỗi tập hợp.
Bài 1 (Trang 65): Cho A = {1, 2, 3, 4, 5}, B = {2, 4, 6, 8}. Tìm A ∪ B, A ∩ B, A \ B.
Giải:
Khi giải các bài tập về tập hợp, cần chú ý đến việc sử dụng đúng các ký hiệu và thuật ngữ. Ngoài ra, cần rèn luyện kỹ năng tư duy logic và khả năng phân tích để giải quyết các bài toán phức tạp.
Hy vọng rằng với những hướng dẫn chi tiết và ví dụ minh họa trên, các em học sinh đã có thể tự tin giải các bài tập trong mục 1 trang 65, 66, 67 SGK Toán 10 tập 1 - Chân trời sáng tạo. Chúc các em học tập tốt!