Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10. Bài viết này sẽ hướng dẫn bạn giải bài 2 trang 35 SGK Toán 10 tập 2 – Chân trời sáng tạo một cách nhanh chóng và hiệu quả.
Chúng tôi cam kết mang đến cho bạn những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và tự tin hơn trong môn Toán.
Khai triển và rút gọn các biểu thức sau:
Đề bài
Khai triển và rút gọn các biểu thức sau:
a) \({\left( {2 + \sqrt 2 } \right)^4}\)
b) \({\left( {2 + \sqrt 2 } \right)^4} + {\left( {2 - \sqrt 2 } \right)^4}\)
c) \({\left( {1 - \sqrt 3 } \right)^5}\)
Phương pháp giải - Xem chi tiết
Sử dụng công thức nhị thức Newton
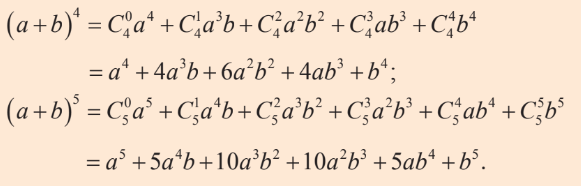
Lời giải chi tiết
a) Áp dụng công thức nhị thức Newton, ta có
\(\begin{array}{l}{\left( {2 + \sqrt 2 } \right)^4} = {2^4} + {4.2^3}.\left( {\sqrt 2 } \right) + {6.2^2}.{\left( {\sqrt 2 } \right)^2} + 4.2.{\left( {\sqrt 2 } \right)^3} + {\left( {\sqrt 2 } \right)^4}\\ = \left[ {{2^4} + {{6.2}^2}.{{\left( {\sqrt 2 } \right)}^2} + {{\left( {\sqrt 2 } \right)}^4}} \right] + \left[ {{{4.2}^3}.\left( {\sqrt 2 } \right) + 4.2.{{\left( {\sqrt 2 } \right)}^3}} \right]\\ = 68 + 48\sqrt 2 \end{array}\)
b) Áp dụng công thức nhị thức Newton, ta có
\({\left( {2 + \sqrt 2 } \right)^4} = {2^4} + {4.2^3}.\left( {\sqrt 2 } \right) + {6.2^2}.{\left( {\sqrt 2 } \right)^2} + 4.2.{\left( {\sqrt 2 } \right)^3} + {\left( {\sqrt 2 } \right)^4}\)
\({\left( {2 - \sqrt 2 } \right)^4} = \left( {2 +(- \sqrt 2 )} \right)^4= {2^4} + {4.2^3}.\left( { - \sqrt 2 } \right) + {6.2^2}.{\left( { - \sqrt 2 } \right)^2} + 4.2.{\left( { - \sqrt 2 } \right)^3} + {\left( { - \sqrt 2 } \right)^4}\)
Từ đó,
\(\begin{array}{l}{\left( {2 + \sqrt 2 } \right)^4} + {\left( {2 - \sqrt 2 } \right)^4} = 2\left[ {{2^4} + {{6.2}^2}.{{\left( {\sqrt 2 } \right)}^2} + {{\left( {\sqrt 2 } \right)}^4}} \right]\\ = 2\left( {16 + 48 + 4} \right) = 136\end{array}\)
c) Áp dụng công thức nhị thức Newton, ta có
\(\begin{array}{l}{\left( {1 - \sqrt 3 } \right)^5} = \left( {1 +(- \sqrt 3 )} \right)^5= 1 + 5.\left( { - \sqrt 3 } \right) + 10.{\left( { - \sqrt 3 } \right)^2} + 10.{\left( { - \sqrt 3 } \right)^3} + 5.{\left( { - \sqrt 3 } \right)^4} + 1.{\left( { - \sqrt 3 } \right)^5}\\ = \left[ {1 + 10.{{\left( { - \sqrt 3 } \right)}^2} + 5.{{\left( { - \sqrt 3 } \right)}^4}} \right] + \left[ {5.\left( { - \sqrt 3 } \right) + 10.{{\left( { - \sqrt 3 } \right)}^3} + 1.{{\left( { - \sqrt 3 } \right)}^5}} \right]\\ = 76 - 44\sqrt 3 \end{array}\)
Bài 2 trang 35 SGK Toán 10 tập 2 – Chân trời sáng tạo thuộc chương trình học Toán 10, tập trung vào việc vận dụng các kiến thức về vectơ trong không gian để giải quyết các bài toán hình học. Bài tập này yêu cầu học sinh phải hiểu rõ các khái niệm như vectơ, phép cộng, phép trừ vectơ, tích của một số với vectơ, và các tính chất của chúng.
Bài 2 trang 35 SGK Toán 10 tập 2 – Chân trời sáng tạo thường bao gồm các dạng bài tập sau:
Để giải bài 2 trang 35 SGK Toán 10 tập 2 – Chân trời sáng tạo một cách hiệu quả, bạn có thể áp dụng các phương pháp sau:
Ví dụ 1: Cho hai vectơ a = (1; 2) và b = (-3; 4). Tính a + b.
Giải:a + b = (1 + (-3); 2 + 4) = (-2; 6)
Ví dụ 2: Cho vectơ a = (2; -1) và số thực k = 3. Tính ka.
Giải:ka = (3 * 2; 3 * (-1)) = (6; -3)
Để củng cố kiến thức và kỹ năng giải bài tập về vectơ, bạn có thể luyện tập thêm với các bài tập tương tự trong SGK Toán 10 tập 2 – Chân trời sáng tạo và các tài liệu tham khảo khác. Hãy chú trọng vào việc hiểu bản chất của bài toán và áp dụng các phương pháp giải phù hợp.
Học Toán đòi hỏi sự kiên trì và luyện tập thường xuyên. Đừng ngại hỏi thầy cô hoặc bạn bè nếu bạn gặp khó khăn trong quá trình học tập. Chúc bạn học tốt môn Toán!
| Khái niệm | Định nghĩa |
|---|---|
| Vectơ | Một đoạn thẳng có hướng. |
| Phép cộng vectơ | Quy tắc hình bình hành hoặc quy tắc tam giác. |
| Tích của một số với vectơ | Một vectơ mới có độ dài bằng tích của số đó với độ dài vectơ ban đầu. |