Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10. Bài viết này sẽ hướng dẫn bạn giải bài 5 trang 39 SGK Toán 10 tập 1 – Chân trời sáng tạo một cách nhanh chóng và hiệu quả.
Chúng tôi cam kết mang đến cho bạn những kiến thức toán học chính xác và hữu ích, giúp bạn tự tin hơn trong quá trình học tập.
ột nông trại thu hoạch được 180 kg cà chua và 15 kg hành tây. Chủ nông trại muốn làm các hũ tương cà để bán. Biết rằng, để làm ra một hũ tương cà loại A cần 10 kg cà chua cùng với l kg hành tây và khi bán lãi được 200 nghìn đồng, còn để làm được một hũ tương cà loại B cần 5 kg cà chua cùng với 0,25 kg hành tây và khi bán lãi được 150 nghìn đồng.
Đề bài
Một nông trại thu hoạch được 180 kg cà chua và 15 kg hành tây. Chủ nông trại muốn làm các hũ tương cà để bán. Biết rằng, để làm ra một hũ tương cà loại A cần 10 kg cà chua cùng với l kg hành tây và khi bán lãi được 200 nghìn đồng, còn để làm được một hũ tương cà loại B cần 5 kg cà chua cùng với 0,25 kg hành tây và khi bán lãi được 150 nghìn đồng. Thǎm dò thị hiếu của khách hàng cho thấy cần phải làm số hũ tương loại A ít nhất gấp 3,5 lần số hũ tương loại B. Hãy giúp chủ nông trại lập kế hoạch làm tương cà để có được nhiều tiền lãi nhất.
Lời giải chi tiết
Gọi x, y lần lượt là số hũ tương cà loại A, loại B mà chủ nông trại cần làm.
Ta có các điều kiện ràng buộc đối với x, y như sau:
- Hiển nhiên \(x \ge 0,y \ge 0\)
- Có 180 kg cà chua nên \(10x + 5y \le 180\)
- Có 15 kg hành tây nên \(x + 0,25y \le 15\)
- Số hũ tương loại A ít nhất gấp 3,5 lần số hũ tương loại B nên \(x \ge 3,5y\)
Từ đó ta có hệ bất phương trình:
\(\left\{ \begin{array}{l}10x + 5y \le 180\\x + 0,25y \le 15\\x \ge 3,5y\\x \ge 0\\y \ge 0\end{array} \right.\)
Biểu diễn từng miền nghiệm của mỗi bất phương trình trên hệ trục tọa độ Oxy.
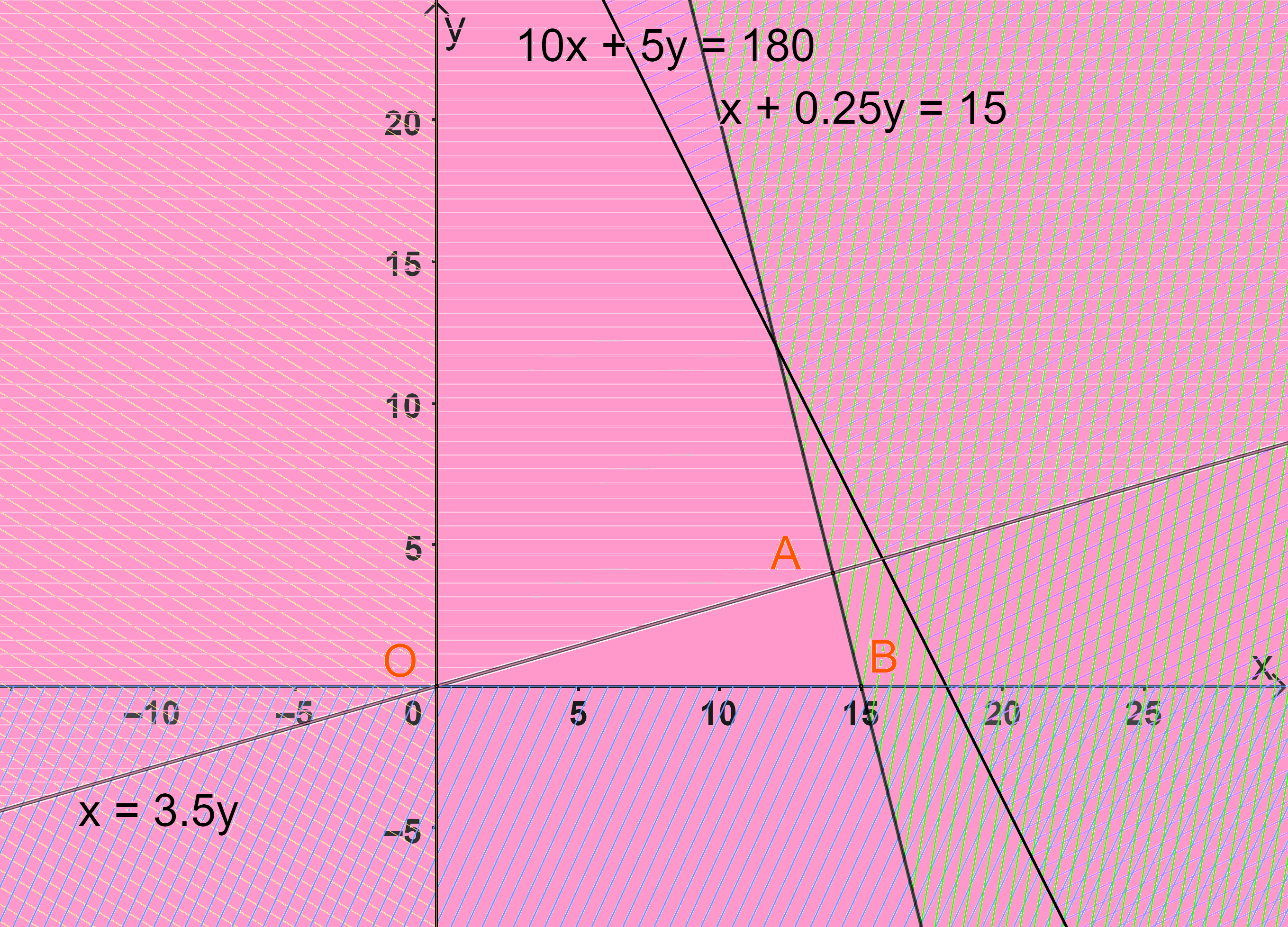
Miền không gạch chéo (miền tam giác OAB, bao gồm cả các cạnh) trong hình trên là phần giao của các miền nghiệm và cũng là phần biểu diễn nghiệm của hệ bất phương trình đã cho.
Với các đỉnh \(O(0;0),A(14;4),\)\(B(15;0).\)
Gọi F là số tiền lãi (đơn vị: nghìn đồng) thu được, ta có: \(F = 200x + 150y\)
Tính giá trị của F tại các đỉnh của tứ giác:
Tại \(O(0;0),\)\(F = 200.0 + 150.0 = 0\)
Tại \(A(14;4),\)\(F = 200.14 + 150.4 = 3400\)
Tại \(B(15;0),\)\(F = 200.15 + 150.0 = 3000\)
F đạt giá trị lớn nhất bằng \(3400\) nghìn đồng tại \(A(14;4).\)
Vậy chủ nông trại đó nên làm 14 hũ loại A và 4 hũ loại B để tiền lãi thu được là lớn nhất.
Bài 5 trang 39 SGK Toán 10 tập 1 – Chân trời sáng tạo thuộc chương trình học Toán 10, tập trung vào việc vận dụng các kiến thức về tập hợp, các phép toán trên tập hợp, và các tính chất cơ bản của tập hợp để giải quyết các bài toán cụ thể. Bài tập này thường yêu cầu học sinh xác định các tập hợp, tìm phần tử thuộc tập hợp, thực hiện các phép hợp, giao, hiệu, bù của các tập hợp, và chứng minh các đẳng thức liên quan đến tập hợp.
Bài 5 thường bao gồm một số câu hỏi nhỏ, mỗi câu hỏi yêu cầu học sinh thực hiện một thao tác cụ thể với tập hợp. Ví dụ:
Để giải quyết hiệu quả các bài tập về tập hợp, bạn cần nắm vững các khái niệm cơ bản và các tính chất của tập hợp. Dưới đây là một số phương pháp giải thường được sử dụng:
Ví dụ: Cho hai tập hợp A = {1, 2, 3, 4} và B = {3, 4, 5, 6}. Hãy tìm A ∪ B, A ∩ B, A \ B, và B \ A.
Giải:
Để củng cố kiến thức và kỹ năng giải bài tập về tập hợp, bạn có thể luyện tập thêm với các bài tập tương tự trong SGK Toán 10 tập 1 – Chân trời sáng tạo và các tài liệu tham khảo khác. Hãy chú trọng việc hiểu rõ bản chất của các khái niệm và các tính chất của tập hợp, và áp dụng linh hoạt các phương pháp giải đã học.
Trong quá trình học tập, nếu gặp khó khăn, đừng ngần ngại hỏi thầy cô giáo hoặc bạn bè để được giúp đỡ. Hãy dành thời gian ôn tập và làm bài tập thường xuyên để nắm vững kiến thức và đạt kết quả tốt nhất.
| Phép toán | Ký hiệu | Định nghĩa |
|---|---|---|
| Hợp | A ∪ B | Tập hợp chứa tất cả các phần tử thuộc A hoặc B |
| Giao | A ∩ B | Tập hợp chứa tất cả các phần tử thuộc cả A và B |
| Hiệu | A \ B | Tập hợp chứa tất cả các phần tử thuộc A nhưng không thuộc B |
| Bù | CAB | Tập hợp chứa tất cả các phần tử thuộc B nhưng không thuộc A |
Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về cách giải bài 5 trang 39 SGK Toán 10 tập 1 – Chân trời sáng tạo. Chúc bạn học tập tốt!